Kezdőlap


Feladat:	1367. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Arányi P. , Babai L. , Balogh K. , Bárány I. , Benkő A. , Darvas Gy. , Deák J. , Domokos L. , Domokos Zsuzsanna , Dömötör P. , Elekes Gy. , Eőry L. , Ferenczi György , Fojt L. , Forgács P. , Gáspár A. , Herényi I. , Herzsényi B. , Hoffmann Gy. , Huhn A. , Juhász F. , Kálmán A. , Kalmár T. , Karosi Gy. , Kiss A. , Korchmáros G. , Lamm P. , Lévai F. , Majtényi G. , Nagy István , Nagy Klára , Racskó P. , Scsaurszky P. , Simig Gy. , Staub Klára , Surányi L. , Sükösd Cs. , Szeidl L. , Székely G. , Szörényi M. , Telegdi L. , Tényi G. , Vermes D. , Vincze T.
Füzet:	1965/október, 74 - 76. oldal		PDF \| MathML
Témakör(ök):	Numerikus és grafikus módszerek, Diszkusszió, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1965/január: 1367. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. A közelítő egyenlőségben szereplő $50^{\circ}$ -os szög a szabályos 9-szög egy oldalához tartozó $40^{\circ}$ -os középponti szögnek pótszöge, ezért közelítőleg ( $5 \cdot 10^{- 5}$ -nél kisebb hibával)

\begin{matrix} cos 40^{\circ} \approx sin 60^{\circ} - 1 / 10, \end{matrix}

másrészt

sin 60^{\circ}

az egységnyi oldalú szabályos háromszög magassága.
Eszerint egy szabályos háromszög magasságából az oldal 1/10 részét kivonva, és a különbség, mint befogó fölé a háromszög-oldallal egyenlő átfogójú derékszögű háromszöget szerkesztve, a befogó melletti szög adja a

40^{\circ}

fenti közelítő értékét. Ennek alapján az

O

középpontú és

r

sugarú körbe az alábbiak szerint szerkeszthetünk közelítőleg szabályos 9-szöget, amelynek egy csúcsa a kör

A

pontj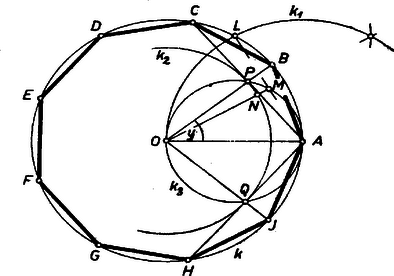a.

Messe

k

-t az

A

körül

r

sugárral írt

k_{1}

kör

L

-ben, az

A L

húrt az

O

-ból rá bocsátott merőleges

M

-ben (e merőleges egy pontját

k_{1}

-ből mindjárt kimetszi az

L

körüli

r

sugarú kör). Mérjük fel

M

-től

O

felé az

r / 10

szakaszt,¹ legyen a végpont

N

. Az

O

körüli

O N

sugarú

k_{2}

kör és az

O A

átmérőjű

k_{3}

kör metszéspontjai legyenek

P

és

Q

. Messe

k

-t az

O P

A P

A Q

O Q

félegyenes rendre a

B

C

H

J

pontban. Ekkor

H

J

A

B

C

a közelítő 9-szög egymás utáni csúcsai.
Nyilvánvaló ugyanis, hogy a

H J

J A

B C

ívek egyenlők

A B

-vel, az utóbbihoz tartozó

A O P

középponti szög pedig közelítőleg

40^{\circ}

, hiszen

A P

merőleges

O P

-re, és így

\begin{matrix} cos A O P = \frac{O P}{O A} = \frac{O N}{O A} = \frac{O M - M N}{O A} = \frac{\sqrt[]{3}}{2} - \frac{1}{10} \approx cos 40^{\circ} . \end{matrix}

A hátra levő csúcsok előállítása végett legyen

k

és a

C

körüli,

C B

sugarú kör új metszéspontja

D

; a további

E

F

G

pontokat pl. a kisebb

H D

ív ismételt felezésével kaphatjuk. Így az

A B C D E F G H J

9-szög körbe írt,

H

-tól

A

-n át

D

-ig menő oldalai egyenlők, és

D

-től

F

-en át

H

-ig menő oldalai ugyancsak egyenlők.

II. Legyen

A O P ∢ = y

. Így

cos y = (5 \sqrt[]{3} - 1) / 10

, és az 1308. feladat megoldásának² gondolatát követve, majd a négyzetgyököt a könnyen adódó, 8 tizedes pontosságú 1,732 050 80 alsó közelítő értékkel pótolva

\begin{matrix} cos 3 y = \frac{15 \sqrt[]{3} - 151}{250} = \frac{60 \sqrt[]{3} - 604}{1000} > - 0, 500 076 96 \end{matrix}

(az utolsó jegyben az abszolút értéket fölkerekítettük), tehát mindenesetre

cos 3 y > - 0, 500 08

.
Tudjuk, hogy

cos 120^{\circ} = - 0, 5000

, és az iskolai négyjegyű függvénytáblázat szerint 4 tizedesre kerekítve

cos 120, 1^{\circ} = - 0, 5015

. Meg akarjuk becsülni, legfeljebb mekkora eltérést okoz

3 y

és

120^{\circ}

között a koszinuszaikban mutatkozó legfeljebb

8 \cdot 10^{- 5}

eltérés. A keresett eltérés akkor adódik legkedvezőtlenebbnek, legnagyobbnak, ha a koszinusz függvény

120^{\circ}

körüli változására azt a legkisebb értéket vesszük alapul (abszolút értékben értve), amire a táblázatból következtetni lehet. A kerekítés miatt

\begin{matrix} - 0, 501 55 \leq cos 120, 1^{\circ} \leq - 0, 501 45, \end{matrix}

eszerint a

120^{\circ}

és

120, 1^{\circ}

közti

0, 1^{\circ}

közre a koszinusz-függvény változása legalább

145 \cdot 10^{- 5}

, ezért ‐ a változást, mint szokás, egyenletesnek véve ‐ a keresett változás legfeljebb

\begin{matrix} \frac{8 \cdot 10^{- 5}}{145 \cdot 10^{- 5}} \cdot 0, 1^{\circ} = \frac{8}{145} \cdot 360'' < 20'' . \end{matrix}

Eszerint

y

kevesebbel haladja meg a

40^{\circ}

-ot, mint

7''

.
Továbbmenve az

A

-t tartalmazó

H O D

szög többlete

200^{\circ}

-hoz képest (amennyinek kellene lennie) kisebb

35''

-nél, a másik

H O D

szög hiánya

160^{\circ}

-hoz képest ugyancsak kisebb, mint

35''

, így a

D

-től

H

-ig terjedő oldalakhoz tartozó középponti szög hiánya

40^{\circ}

-hoz képest kisebb

9''

-nél, ami a középponti szög pontos értékének 1/16 000 része.

Ferenczi György (Budapest, I. István g. IV. o. t.)

¹Ennek megszerkesztését itt nem részletezzük; egy lehetőséget ad a 961. gyakorlat, kitűzését lásd K. M. L. 30 (1965) 28. o.

²K. M. L. 30 (1965) 113. o.