Feladat: 1358. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Balogh Kálmán ,  Domokos Zsuzsa 
Füzet: 1965/november, 153 - 155. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Sokszögek súlypontjának koordinátái, Egyenesek egyenlete, Parabola egyenlete, Osztópontok koordinátái, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1964/december: 1358. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Helyezzünk koordinátarendszert az ábrára, tengelyeknek a négyzet középvonalait véve. Legyen a kettévágó egyenes egyenlete y=mx. A szimmetria miatt elég a -1≤m≤1 értékekre szorítkoznunk és a kettévágott négyzet alsó felének súlypontját tekintenünk, hiszen a felső rész ebből 180∘-os forgatással áll elő, ha pedig a kettévágó szakasz az Y-tengellyel zár be kisebb szöget (és így |m|>1), akkor a már vizsgált esetnek az egyik átlón való tükörképével állunk szemben.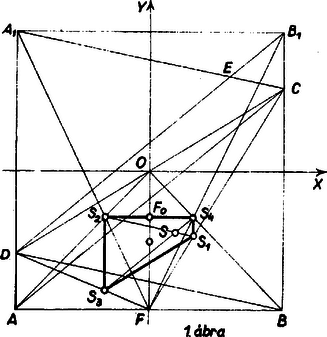
Legyen a négyzet alsó két csúcsa A(-3;-3) és B(3;-3), ekkor az alsó trapéz további két csúcsa C(3;3m) és D(-3;-3m).
 
 
A trapézt az AC átlóval kettévágva az ACB háromszög súlypontja S1(1;m-2), az ACD háromszögé pedig az állandó OA súlyvonalat harmadoló S2(-1;-1) pont. A trapéz keresett S(x,y) súlypontja rajta van e két súlypont összekötő egyenesén, tehát kielégíti az S1S2 egyenes egyenletét:
y=m-12(x+1)-1.
Hasonlóan a BD átlóval való kettévágás után a BDA háromszög S3(-1;-m-2) súlypontját a BDC háromszög S4(1;-1) súlypontjával összekötő egyenes egyenletét is kielégítik S koordinátái:
y=m+12(x-1)-1.

A két összefüggésből
x=m,y=m2-32.

Így az ABCD trapéz súlypontjának mértani helye (m kiküszöbölésével) az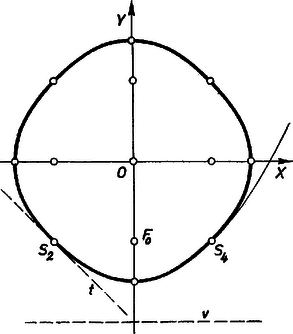
y=x22-32,-1≤x≤1
parabolaív.
 
 
2. ábra
 

A parabola csúcsa az AB-re merőleges oldalfelező (0;-3/2) alsó negyedelő pontja, tengelye ez az oldalfelező, F0 fókusza a (0;-1) pont, az oldalfelező alsó harmadoló pontja, vezéregyenese az oldalfelezőt alsó 6-od-részében metszi. A parabolaív végpontjai S2 és S4, ugyanis m=-1 esetén az ABC, m=1 esetén pedig az ABD háromszög elfajul a négyzet AB oldalává, tömege 0-ra csökken.
S2-ben és S4-ben a parabolaív félérintője 45∘ szöggel hajlik a tengelyhez, vagyis párhuzamos a B-ből, ill. A-ból kiinduló átlóval. Ennélfogva az első bekezdésben vázolt teljes mértani helynek, a 4 parabolaívből álló, 4 tengelyű, zárt görbe vonalnak a csatlakozási pontokban is van érintője.
 
Domokos Zsuzsanna (Makó, József A. g. III. o. t.)
 

II. megoldás. Az előző megoldás jelöléseit használva ismét csak a négyzet AB oldalára merőleges oldalakat metsző egyenesekkel lemetszett ABCD trapézok S súlypontját vizsgáljuk. A négyzet másik két csúcsa legyen B1 és A1, az AB szakasz felezőpontja F. Ekkor S2, mint az AO szakasz O felőli harmadoló pontja, az ABA1 háromszögnek is súlypontja, így S2 az A1F szakasz F felőli harmadoló pontja, és hasonlóan S4 a B1F szakasz F felőli harmadoló pontja. Az S2S4S1S3 trapéz tehát az A1B1CD trapéz F-ből harmadára kicsinyített képe. Elég tehát az utóbbi trapéz átlói E metszéspontjának a mértani helyét vizsgálni.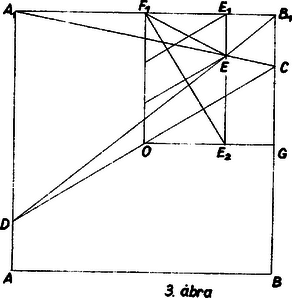
 
 

Messe az E-ből A1B1-re bocsátott merőleges A1B1-et E1-ben, akkor az A1ED, CEB1 hasonló háromszögekből, továbbá a párhuzamosokkal elmetszett A1B1D szögből kapjuk, hogy
A1DCB1=DEEB1=A1E1E1B1.
Másrészt viszont A1E1+E1B1=A1D+DA=A1D+CB1, így kell hogy E1B1=CB1 (és A1E1=A1D) legyen. Legyen O merőleges vetülete B1C-n G, E vetülete OG-n E2. Ekkor a B1F1OG négyzetet középpontja körül 90∘-kal elforgatva F1E2 átmegy OC-be, a két egyenes tehát merőleges egymásra.
Ismeretes, hogy a trapéz párhuzamos oldalaival párhuzamosan húzott E1E2 egyenes trapézba eső részét az átlók E metszéspontja felezi. Húzzunk E1-ből párhuzamost CD-vel, ekkor az OF1 és E1E2 közt paralelogramma keletkezik, melynek az E-ből húzott középvonala felezi az F1E2 paralelogrammába eső szakaszát és merőleges rá, mivel párhuzamos OC-vel; ez az egyenes felezi az F1E2 szakaszt is, mert annak a két végén egyenlő szakaszai esnek a paralelogrammán kívül is, így ez az E1E2 szakasz felező merőlegese, tehát EE2=EF1.
Ezzel beláttuk, hogy E annak a parabolának az AA1B1B négyzetbe eső ívén van, amelyiknek gyújtópontja F1, irányvonala az OG egyenes. Ha E ennek az ívnek tetszés szerinti pontja, D az AA1 és B1E egyenesek metszéspontja, C pedig DO és BB1 metszéspontja, akkor az előbbi meggondolás szerint az A1B1CD trapéz átlóinak metszéspontja a parabola íven van, és természetesen a B1D egyenesen is, tehát az E pont lesz az. Ezt az ívet F-ből harmadára kicsinyítve az előbbi megoldásban leírt mértani helyhez jutunk.
 

 Balogh Kálmán (Budapest, Fazekas M. gyak. g. II. o. t.) dolgozata,
 kiegészítésekkel.