Kezdőlap


Feladat:	1357. matematika feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Sebő Imre , Tóth Teréz
Füzet:	1965/december, 206 - 207. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Magasságvonal, Hozzáírt körök, Diszkusszió, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1964/december: 1357. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az adott $ϱ_{a}$ , ill. $ϱ_{b}$ az $A B C Δ$ $B C$ , ill. $C A$ oldalszakaszát és a másik 2‐2 oldal meghosszabbítását érintő kör sugara, továbbá adott az $A B$ oldalhoz tartozó $m_{c}$ magasság. Legyen a két kör középpontja $O_{a}$ , ill. $O_{b}$ , és érintési pontjuk a $B C$ oldalegyenesen 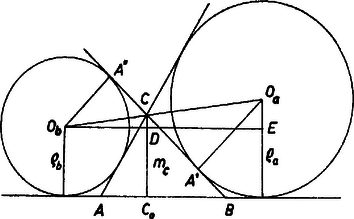$A'$ , ill. $A''$ .

C O_{a}

és

C O_{b}

felezi a háromszög

C

-nél levő egyik-egyik külső szögét, tehát egymás meghosszabbításába esnek. Így

C O_{a} A'

és

C O_{b} A''

hasonló derékszögű háromszögek, ezért

\begin{matrix} \frac{C O_{a}}{C O_{b}} = \frac{O_{a} A'}{O_{b} A''} = \frac{ϱ_{a}}{ϱ_{b}} . \end{matrix}

(1)

Messe az

O_{b}

-n átmenő,

A B

-vel párhuzamos egyenes a

C

-ből és

O_{a}

-ból

A B

-re bocsátott merőlegest a

D

, ill.

E

pontban.

ϱ_{a} > ϱ_{b}

esetén

D

C C_{0}

magasságszakaszon van. Felhasználva az

O_{b} C D

és

O_{b} O_{a} E

háromszögek hasonlóságát és (1)-et

\begin{matrix} C D = \frac{C O_{b}}{O_{a} O_{b}} \cdot O_{a} E = \frac{C O_{b}}{O_{a} C + C O_{b}} \cdot O_{a} E = \frac{1}{\frac{C O_{a}}{C O_{b}} + 1} \cdot O_{a} E, \\ m_{c} - ϱ_{b} = \frac{1}{1 + ϱ_{a} / ϱ_{b}} \cdot (ϱ_{a} - ϱ_{b}), amiből \\ m_{c} = \frac{2 ϱ_{a} ϱ_{b}}{ϱ_{a} + ϱ_{b}} . & (2) \end{matrix}

Ha pedig

ϱ_{a} = ϱ_{b}

, akkor az

O_{a} C O_{b}

egyenes párhuzamos

A B

-vel, és ezért

m_{c} = ϱ_{a} = ϱ_{b}

, s így a (2) eredmény erre a speciális esetre is helyes.
Ezek szerint

m_{c}

egyik esetben sem független az adott sugaraktól, a háromszög az adatokból nem szerkeszthető meg egyértelműen. Ha az adathármas teljesíti (2)-t (ez annyi, mintha csak két adat lenne), így végtelen sok megfelelő háromszög szerkeszthető (az

A B

egyenes egyik partján úgy vesszük fel a két érintő kört, hogy ne legyen közös pontjuk, a háromszög további két oldalegyenesét a két kör közös belső érintői adják). Ha pedig (2) nem teljesül, egyetlen háromszög sem tesz eleget a követelményeknek.

Tóth Teréz (Makó, József A. g. III. o. t.)

II. megoldás. Az adott sugarak és a magasság ismert módon kifejezhetők a háromszög

t

területével,

a

b

c

oldalaival és

a + b + c = 2 s

kerületének felével:

\begin{matrix} ϱ_{a} = \frac{t}{s - a}, ϱ_{b} = \frac{t}{s - b}, m_{c} = \frac{2 t}{c} . \end{matrix}

Innen egyrészt

\begin{matrix} c = 2 s - (a + b) = (s - a) + (s - b) = \frac{t}{ϱ_{a}} + \frac{t}{ϱ_{b}}, \end{matrix}

másrészt

c = \frac{2 t}{m_{c}}

, és a két kifejezés egyenlőségéből

\begin{matrix} \frac{1}{m_{c}} = \frac{1}{2} (\frac{1}{ϱ_{a}} + \frac{1}{ϱ_{b}}) \end{matrix}

(tekintet nélkül a két sugár nagyságviszonyára).
Ebből ugyanaz a következtetés adódik, mint az I. megoldásban.

Sebő Imre (Pannonhalma, Benedek-rendi g. II. o. t.)