Kezdőlap


Feladat:	1354. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Arányi P. , Bárány Imre , Baranyai Zs. , Deák J. , Domokos L. , Domokos Zsuzsanna , Eff L. , Ferenczi Gy. , Fodor Magdolna , Gáspár A. , Herszényi B. , Huhn A. , Karsai Kornélia , Lévai F. , Majtényi G. , Malina J. , Márki L. , Molnár Ágnes , Palotás Á. , Scsaurszky Péter , Simig Gy. , Staub Klára , Szabó István , Székely G. , Szörényi M. , Tényi G.
Füzet:	1965/október, 67 - 70. oldal		PDF \| MathML
Témakör(ök):	Egyenletrendszerek grafikus megoldása, Harmadfokú (és arra visszavezethető) egyenletrendszerek, Kör egyenlete, Egyéb ponthalmazok a koordinátasíkon, Síkbeli szimmetrikus alakzatok, Feladat
Hivatkozás(ok):	Feladatok: 1964/december: 1354. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) (1)-ből $y$ fejezhető ki könnyen, (2)-ből pedig 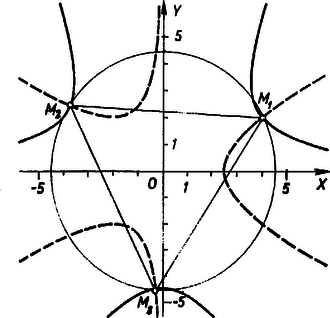$x$ .

\begin{matrix} y = \pm \sqrt[]{\frac{x^{2}}{3} - \frac{16}{3 x}}, x = \pm \sqrt[]{\frac{y^{2}}{3} - \frac{88}{3 y}}, \end{matrix}

ezek alapján az ábra 3‐3 ágból álló görbéit kapjuk,(1) görbéje szaggatott vonallal van rajzolva. Az (1) görbe az

X

-tengelyre szimmetrikus, a (2) pedig az

Y

-ra. Nem kapunk

y

-t (1)-ből, ha

0 \leq x^{3} < 16

, és

x

-et (2)-ből, ha

- 88 < y^{3} \leq 0

. (Az (1) görbének aszimptotája az

Y

-tengely, (2)-nek pedig az

X

-tengely.) Az értéktáblázatot

0, 5

hosszúságú lépésekben készítve és a grafikon hosszegységét 1 cm-nek véve (ábránk ennek

1 : 2

arányú kicsinyítettje) a metszéspontok koordinátái, vagyis a gyökök kb. milliméter, azaz egy tizedes jegy pontossággal olvashatók le. Már az értéktáblázatból kiolvasható, hogy az

x_{1} = 4

y_{1} = 2

koordinátájú

M_{1}

pont mindkét görbén rajta van, tehát ez az értékpár pontos megoldás. Az ábra két további metszéspontot mutat, ezekből két közelítő megoldást olvashatunk le:

\begin{matrix} x_{2} \approx - 3, 7, y_{2} \approx 2, 5; és x_{3} \approx - 0, 3, y_{3} \approx - 4, 5. \end{matrix}

b) Az egyenletrendszerből a konstans tagokat kiküszöbölve ‐ vagyis (1)-et 11-gyel, (2)-t (

- 2

)-vel szorozva és összeadva ‐ homogén harmadfokú egyenlet adódik, abból pedig pl.

x^{3}

-nel való osztás útján az

y / x = z

hányadosra kapunk harmadfokú ogyenletet:

\begin{matrix} 11 x^{3} - 6 x^{2} y - 33 x y^{2} + 2 y^{3} = 0, 2 z^{3} - 33 z^{2} - 6 z + 11 = 0. \end{matrix}

Tudjuk, hogy ennek az egyenletnek egyik gyöke

z_{1} = y_{1} / x_{1} = 1 / 2

, ezért a bal oldalból kiemelhető a megfelelő

z - 1 / 2

, s így ennek 2-szerese is, a

2 z - 1

gyöktényező. Valóban

\begin{matrix} 2 z^{3} - 33 z^{2} - 6 z + 11 = z^{2} (2 z - 1) - 32 z^{2} - 6 z + 11 = \\ = z^{2} (2 z - 1) - 16 z (2 z - 1) - (22 z - 11) = (2 z - 1) (z^{2} - 16 z - 11), \end{matrix}

így a további két gyök a

z^{2} - 16 z - 11 = 0

egyenletből

z_{2,3} = 8 \pm 5 \sqrt[]{3}

.
Mármost

y = z x = (8 \pm 5 \sqrt[]{3}) x

helyettesítéssel (1)-ből

\begin{matrix} x_{2,3}^{3} (1 - 3 z^{2}) = x_{2,3}^{3} (- 416 \mp 240 \sqrt[]{3}) = 16, \\ x_{2,3} = \sqrt[3]{\frac{16}{- 416 \mp 240 \sqrt[]{3}}} = \sqrt[3]{\frac{1}{- 26 \mp 15 \sqrt[]{3}}} = \sqrt[3]{- 26 \pm 15 \sqrt[]{3}}, \end{matrix}

és így

\begin{matrix} y_{2,3} = \sqrt[3]{{(8 \pm 5 \sqrt[]{3})}^{3} (- 26 \pm 15 \sqrt[]{3})} = \sqrt[3]{- 37 \mp 30 \sqrt[]{3}} . \end{matrix}

Megpróbáljuk előállítani

x_{2,3}

-t

c \pm d \sqrt[]{3}

alakban, ahol

c

és

d

egész szám. Ez sikerül, így ugyanis

\begin{matrix} x^{3} = c (c^{2} + 9 d^{2}) \pm 3 d (c^{2} + d^{2}) \sqrt[]{3}, \end{matrix}

és a

\begin{matrix} c (c^{2} + 9 d^{2}) = - 26, 3 d (c^{2} + d^{2}) = 15 \end{matrix}

egyenletrendszernek megoldása

c = - 2

d = 1

. Ennélfogva

\begin{matrix} x_{2,3} = - 2 \pm \sqrt[]{3}, és ebből y_{2,3} = z_{2,3} \cdot x_{2,3} = - 1 \mp 2 \sqrt[]{3}, \end{matrix}

két tizedes pontossággal

\begin{matrix} x_{3} \approx - 0, 27, y_{3} \approx - 4, 46; x_{2} \approx - 3, 73, y_{2} \approx 2, 46; \end{matrix}

ami a grafikus megoldást igazolja.

II. megoldás a b) részre. Az ábráról úgy látszik, hogy

M_{1}

M_{2}

és

M_{3}

egy origó középpontú körön vannak, a leolvasott közelítő értékekből is

\begin{matrix} x_{1}^{2} + y_{1}^{2} = 20, x_{2}^{2} + y_{2}^{2} \approx 20, 34, x_{3}^{2} + y_{3}^{2} \approx 19, 94, \end{matrix}

közel egyenlők. Bebizonyítjuk, hogy ez a sejtés helyes.
(1) és (2) négyzetében csak páros kitevős hatványok lépnek fel, és a bal oldalak összegében felismerjük a négyzetösszeg köbét:

\begin{matrix} x^{2} (x^{4} - 6 x^{2} y^{2} + 9 y^{4}) + y^{2} (9 x^{4} - 6 x^{2} y^{2} + y^{4}) = \\ = x^{6} + 3 x^{4} y^{2} + 3 x^{2} y^{4} + y^{6} = {(x^{2} + y^{2})}^{3} = 8000 = 20^{3} . \end{matrix}

Eszerint ha egy

x

y

értékpár (1)-et is, (2)-t is kielégíti, akkor teljesül rá az egyszerűbb

x^{2} + y^{2} = 20

egyenlet is.
Ennek alapján (1)-ből

y

-t kiküszöbölve és az adódó egyenlet 0-ra redukált alakjának bal oldalát az ismert

x_{1} = 4

-hez tartozó gyöktényezővel osztva

\begin{matrix} x^{3} - 15 x - 4 = 0; x^{3} - 15 x - 4 = x^{2} (x - 4) + 4 x^{2} - 15 x - 4 = \\ = x^{2} (x - 4) + 4 x (x - 4) + (x - 4) = (x - 4) (x^{2} + 4 x + 1), \end{matrix}

és az

x^{2} + 4 x + 1 = 0

egyenletből

x_{2,3} = - 2 \pm \sqrt[]{3}

. Továbbá (2)-ből

\begin{matrix} y_{2,3} = \frac{88}{3 x^{2} - y^{2}} = \frac{22}{x^{2} - 5} = \frac{22}{2 \mp 4 \sqrt[]{3}} = \frac{11}{1 \mp 2 \sqrt[]{3}} = - 1 \mp 2 \sqrt[]{3} . \end{matrix}

Bárány Imre (Budapest ‐ Mátyásföld, Corvin M. g. III. o. t.)

III. megoldás a b) részre. Az ábráról úgy látszik, hogy

M_{1} M_{2} M_{3}

egyenlő oldalú háromszög, sőt hogy a két görbe 3‐3 ága előáll egymásból

120^{\circ}

-os forgatásokkal az origó körül. Bebizonyítjuk az utóbbi sejtés helyességét avval, hogy ha

P (x

y

) bármelyik görbe egy pontja, akkor a

120^{\circ}

-kal elforgatott

P' (x'

y'

) pont is rajta van az illető görbén.
Legyen

P

-nek az origótól való távolsága

r

, és az

X

-tengely pozitív felét az

O P

félegyenesbe vivő forgás szöge

φ

; ekkor

x = r cos φ

y = r sin φ

\begin{matrix} x' = r cos (φ + 120^{\circ}) = - \frac{r}{2} cos φ - \frac{r \sqrt[]{3}}{2} sin φ = \frac{1}{2} (- x - y \sqrt[]{3}), & (3) \\ y' = r sin (φ + 120^{\circ}) = \frac{1}{2} (- y + x \sqrt[]{3}) . \end{matrix}

Ezeket írva (1) és (2) bal oldalán

x

, ill.

y

helyébe, a kifejezések az eredeti bal oldalakba mennek át:

\begin{matrix} x' (x'^{2} - 3 y'^{2}) & = \frac{- x - y \sqrt[]{3}}{2} \cdot \frac{- 8 x (x - y \sqrt[]{3})}{4} = x (x^{2} - 3 y^{2}), \\ y' (3 x'^{2} - y'^{2}) & = \frac{- y + x \sqrt[]{3}}{2} \cdot \frac{8 y (x \sqrt[]{3} + y)}{4} = y (3 x^{2} - y^{2}), \end{matrix}

és ez állításunkat bizonyítja.
Ezek szerint

M_{1}

koordinátáiból (3) alapján kiszámíthatjuk

M_{2}

-éit, majd ezekből

M_{3}

-éit. Így is a fenti megoldásokat kapjuk.

Scsaurszky Péter (Pannonhalma, Benedek-rendi g. IV. o. t.)

Megjegyzés.

x = r cos φ

y = r sin φ

helyettesítéssel és a trigonometrikus kifejezések felismerésével (1) és (2) így írható:

\begin{matrix} r^{3} cos 3 φ = 16, r^{3} sin 3 φ = 88. \end{matrix}

Eszerint a görbék polárkoordinátás egyenlete:

\begin{matrix} r = \sqrt[3]{\frac{16}{cos 3 φ}}, ill. r = \sqrt[3]{\frac{88}{sin 3 φ}} . \end{matrix}

Ez is mutatja a forgási szimmetriát, hiszen

φ

-t

120^{\circ}

-kal növelve

3 φ

növekedése

360^{\circ}

, a nevezők és

r

értéke nem változik.
Innen is látható, hogy (1)-nek az

O

-n átmenő

60^{\circ}

-os és

300^{\circ}

-os forgásszögű egyenesek is szimmetriatengelyei, (2)-nek pedig a

30^{\circ}

-os és

150^{\circ}

-os egyenesek, továbbá az utóbbi két egyenes (1)-nek, az előbbi kettő (2)-nek aszimptotája. Az (1) görbét

30^{\circ}

-kal elforgatva, valamint 88 és 16 köbgyökének arányában nyújtva a (2)-t kapjuk.

Molnár Ágnes (Budapest ‐ Cinkota, Kultúrház utcai g. IV. o. t.)