Kezdőlap


Feladat:	1352. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Majtényi Gábor , Márki László
Füzet:	1965/október, 64 - 66. oldal		PDF \| MathML
Témakör(ök):	Súlypont, Magasságpont, Hiperbola egyenlete, Hiperbola, mint kúpszelet, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1964/november: 1352. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Feltesszük, hogy az $S$ súlypont és az $M$ magasságpont különböző, mert különben a szimmetriatengely bármely $S$ -en átmenő egyenes lehet, minden $S$ középpontú szabályos $A B C$ háromszög megfelel a feladat követelményeinek, tehát a mértani hely az egész sík, $S$ kivételével.
Miután $S$ és $M$ a szimmetriatengelyen van, $S M$ maga a szimmetriatengely, ezen mozog a $C$ csúcs, az alap erre merőleges és félakkora távolságra van $S$ -től, mint $C$ . Válasszuk a derékszögű koordinátarendszer origójának $S$ -et, $Y$ tengelyének az $S M$ egyenest, $M$ ordinátáját 1-nek, és legyenek ezeknek megfelelően $A$ és $B$ koordinátái ( $x$ , $y$ ), és ( $- x$ , $y$ ). Ekkor $C$ koordinátái ( $0$ , $- 2 y$ ).
A $C A$ szár és a $B M$ magasság merőlegesek, ez akkor és csak akkor teljesül, ha iránytangenseik szorzata $- 1$ , tehát ha $x \neq 0$ , és

\begin{matrix} \frac{y - (- 2 y)}{x} \cdot \frac{1 - y}{x} = \frac{3 y (1 - y)}{x^{2}} = - 1. \end{matrix}

Mivel

x

nem 0, átszorozhatunk a négyzetével és rendezhetjük az egyenletet. A mértani hely tehát azokból a pontokból áll, amelyeknek koordinátáira

\begin{matrix} 3 y^{2} - 3 y - x^{2} = 0, x \neq 0. \end{matrix}

(1)

Egyenletünk így is írható:

\begin{matrix} 3 {(y - \frac{1}{2})}^{2} - x^{2} = \frac{3}{4}, - \frac{x^{2}}{\frac{3}{4}} + \frac{{(y - \frac{1}{2})}^{2}}{^{\frac{1}{4}}} = 1. \end{matrix}

Eszerint

A

és

B

mértani helye az a hiperbola, az

Y

tengelyen levő pontjai kivételével, amelyiknek középpontja a (0, 1/2) pont ‐ vagyis az

S M

szakasz felezőpontja ‐, főtengelye az

Y

tengely ‐ más szóval az SM egyenes ‐, fő-, ill. melléktengelye felének hossza

(a =)

1/2, ill.

(b =)

\sqrt[]{3} / 2

, ezért csúcsai

S

és

M

(ezek nem tartoznak a mértani helyhez), fókuszainak távolsága a középponttól 1(ti.

a^{2} + b^{2}

négyzetgyöke), másrészt aszimptotái a főtengellyel

60^{\circ}

-os szöget zárnak be.
Meg kell azonban jegyezni, hogy az

S M

egyenesen végigfutó

C

pontnak nem minden helyzetéhez tartozik háromszög. (1)-ből

x^{2} = 3 y (y - 1)

negatív, ha

0 < y < 1

, másrészt a fent kizárt

x = 0

esetben (és csak ekkor)

y = 0, 1

. Eszerint

C

ordinátájára vagy

- 2 y > 0

, vagy

- 2 y < - 2

, tehát míg

C

az ábra

S E

szakaszán halad végig, nem jön létre háromszög.

Majtényi Gábor (Pannonhalma, Benedek-rendi g. IV. o. t.)

II. megoldás. A mértani helyet megállapíthatjuk koordináta geometria felhasználása nélkül is, ha már elég sok pont megszerkesztése után kialakult, hogy milyen görbét várhatunk megoldásul.
Jegyezzük meg először is, hogy az

S

súlyponttal és

M

magasságponttal együtt a háromszög köré írt kör

K

középpontja is közös a szóban forgó egyenlő szárú háromszögekben.

K

-t ugyanis megkaphatjuk pl. mint a

B C

oldalra

A_{1}

felezőpontjában emelt merőlegesnek az

S M

egyenessel való metszéspontját. Ekkor azonban az

A S M

és

A_{1} S K

hasonló háromszögekből

S K / S M = S A_{1} / S A = 1 / 2

S K = S M / 2

, és

S

K

és

M

pontok közt van, miután

A

-t és

A_{1}

-et is elválasztja¹. Eszerint

C

egy bizonyos helyzetéhez tartozó

A

B

pontpár csak a

K

körül

K C

sugárral írt körön kereshető. Másrészt

A B

-nek

D

felezőpontja

C S

-nek

S

-en túli meghosszabbításán

C D = 3 C S / 2

távolságra van,

A

és

B

pedig a

D

-ben

S M

-re állított merőlegesen. Ezek szerint

A

és

B

a merőlegesnek a fenti körrel való metszéspontjai.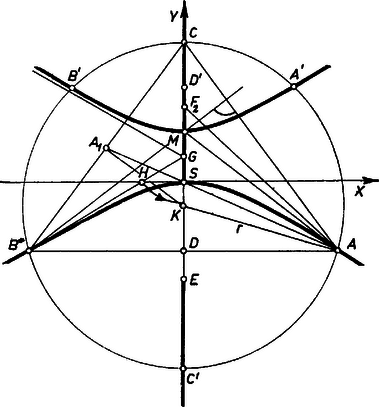

Egy

K

közepű kör kétszer metszi

S M

-t, ezért egy ilyen kört ‐ ha

K C > K M

‐ egy csapásra két

A

B

pontpár szerkesztésében használhatunk fel. (

K S < K C < K M

esetén csak egyik

C

helyzethez kapunk így

A

B

-t,

K C < K S

esetén pedig egyikhez sem.

K C = K S

esetén szakasszá elfajult háromszög adódik, ugyanígy

K C = K M

esetén az egyik

C

helyzethez. Ismét adódik, hogy az

S K

négyszeresére nyújtásával kapott

S E

szakaszon levő

C

-k nem adnak háromszöget.) A pontpárokat szaporítva hiperbola látszik kialakulni, melynek csúcsai

S

és

M

. Ha sejtésünk helyes, az

S M

szakasz

G

középpontját az ábra ,,távoli''

B^{*}

pontjával összekötő egyenes közel áll az egyik aszimptotához, azért az

S

-ben

S M

-re állított merőlegessel (a csúcsérintővel) való

H

metszéspontját

G

körül

S M

-re forgatva az egyik fókuszhoz közeli pontot kell kapnunk.² A forgatás

K

-hoz közel eső pontot ad, ezért megpróbáljuk bebizonyítani, hogy a mértani hely az a hiperbola, melynek csúcsai

M

és

S

, és egyik fókusza

K

(így a másik fókusz

K

-nak

G

-re vonatkozó

F_{2}

tükörképe).
Legyen

C

S M

-nek

M

-en túli meghosszabbításán ‐ így

D

S K

-nak

K

-n túli meghosszabbításán van ‐, és legyen

K C = K A = r

, továbbá

S M = 2 a

, így

F_{2} M = S K = a

\begin{matrix} F_{2} A^{2} = F_{2} D^{2} + D A^{2} = F_{2} D^{2} + K A^{2} - K D^{2} = K A^{2} + (F_{2} D + K D) F_{2} K, \end{matrix}

ehhez

F_{2} D = F_{2} S + S D

K D = S D - S K

, ezért

\begin{matrix} F_{2} D + K D = 2 a + 2 S D = 2 a + C S = 2 a + (r - a) = r + a; \\ F_{2} A^{2} = r^{2} + (r + a) 4 a = {(r + 2 a)}^{2}, \\ F_{2} A = r + 2 a, vagyis F_{2} A - K A = 2 a = S M, \end{matrix}

amit bizonyítani akartunk.
Csekély közbülső eltérések után ugyanerre az eredményre jutunk, ha

C

S M

szakaszon van, ha pedig

S E

-nek

E

-n túli meghosszabbításán van

C

, akkor

K A - F_{2} A = 2 a

.
Hasonlóan meg lehet mutatni, hogy ha

F_{2} K = 4 a

, és

F_{2} A - K A = 2 a

, vagy

K A - F_{2} A = 2 a

, de

A

nincs

F_{2} K

-n, továbbá a

C

pontot úgy jelöljük ki a

K F_{2}

egyenesen, hogy

A

-nak

D

vetületétől 3-szor annyira legyen, mint

S

K F_{2}

szakasz első negyedelő pontja), és ugyanazon az oldalon,

B

pedig

A

tükörképe

D

-re, akkor

K C = K A

, tehát

K

A B C

egyenlő szárú háromszög köré írt kör középpontja,

S

a súlypontja, és így

M

a magasságpontja; tehát

A

hozzátartozik a mértani helyhez.

Márki László (Budapest, Fazekas M. gyak. g. IV. o. t.)

¹Minden háromszögre igaz, hogy

M

S

és

K

egy egyenesen van, a háromszög ún. Euler-egyenesén és

S K = S M / 2

. Lásd pl. Gallai T.‐Hódi E.‐Szabó P.‐Tolnai J.: Matematika az ált. gimn. III. o. számára, 12. kiadás, Tankönyvkiadó, Budapest, 1962, 163. o.

²Ugyanis a hiperbola középpontja körüli, a fókuszokon átmenő kör átmegy a csúcsérintők és aszimptóták metszéspontjain is.