Kezdőlap


Feladat:	1349. matematika feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Rodler Erzsébet
Füzet:	1965/november, 139 - 140. oldal		PDF \| MathML
Témakör(ök):	Kör geometriája, Egyenlő szárú háromszögek geometriája, Hossz, kerület, Terület, felszín, Feladat
Hivatkozás(ok):	Feladatok: 1964/november: 1349. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a körcikk csúcsa $O$ , ívének egyik végpontja $A$ , felezőpontja $C$ , és messe a kettévágó egyenes a körcikk kerületének $O$ és $C$ közti, $A$ -n átmenő darabját $A'$ -ben. A keletkezett két rész kerületeinek nem közös részei is egyenlők, ezért $A'$ felezi az $O A$ sugárból és $A C$ ívből álló vonaldarabot. $A C$ a kör kerületének $12$ -ed része, és így kisebb a sugárnál, ezért $A'$ az $O A$ szakaszon van. Így a körcikk $O$ -t tartalmazó része egyenlő oldalú háromszög. Megmutatjuk, hogy e háromszög és a körcikk területének aránya kisebb $1 / 2$ -nél, tehát a háromszög a kisebb területű rész.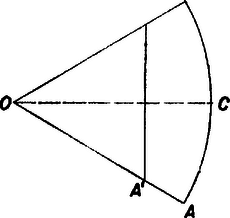

O A = r

és

O A' = a

jelöléssel

\begin{matrix} a' = \frac{1}{2} (r + \frac{2 π r}{12}) = \frac{6 + π}{12} \cdot r (\approx 0, 762 r), \end{matrix}

így a kérdéses arány

\begin{matrix} k = \frac{a^{2} \sqrt[]{3}}{4} : \frac{r^{2} π}{6} = \frac{3 \sqrt[]{3}}{2 π} \cdot {(\frac{a}{r})}^{2} = \frac{3 \sqrt[]{3}}{2 π} {(\frac{6 + π}{12})}^{2} . \end{matrix}

Mivel egyrészt

\begin{matrix} \sqrt[]{3} < 7 / 4, hiszen 3 < 49 / 16, \end{matrix}

másrészt, mint ismeretes,

\begin{matrix} 3, 125 = 25 / 8 < π < 22 / 7 = 3, 1428 ... \end{matrix}

azért

k

számlálójának tényezőit növelve, nevezőjét pedig csökkentve

\begin{matrix} k < \frac{3}{2} \cdot \frac{7}{4} \cdot \frac{8}{25} {(\frac{6 + 22 / 7}{12})}^{2} = \frac{21}{25} \cdot {(\frac{16}{21})}^{2} = \frac{16^{2}}{25 \cdot 21} = \frac{256}{525} < \frac{1}{2}, \end{matrix}

amit bizonyítani akartunk.

Rodler Erzsébet (Székesfehérvár, Ybl M. g. III. o. t.)