Kezdőlap


Feladat:	1341. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Nagy Sarolta
Füzet:	1965/szeptember, 26 - 27. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Algebrai átalakítások, Beírt kör, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1964/október: 1341. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ismeretes, hogy a háromszögbe írt $k$ kör $ϱ$ sugara egyenlő a $t / s$ hányadossal, ahol $t$ a terület, $s$ pedig a kerület fele.

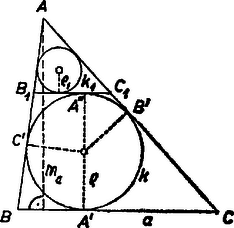
a

oldallal párhuzamos érintő által lemetszett

H_{1}

háromszög hasonló az eredeti

H

háromszöghöz, így a beleírt

k_{1}

kör

ϱ_{1}

sugara ugyanannyiad része

ϱ

-nak, mint

H_{1}

valamelyik hosszúsági mérete

H

megfelelő méretének. Célszerű az

a

oldalra merőleges

m_{a 1}

és

m_{a}

magasságok arányát vennünk, mert

m_{a 1} = m_{a} - 2 ϱ

. Másrészt

m_{a} = 2 t / a

, így

\begin{matrix} m_{a 1} = \frac{2 t - 2 a ϱ}{a}, és ϱ_{1} = \frac{t - a ϱ}{t} \cdot ϱ = ϱ - \frac{ϱ^{2}}{t} a . \end{matrix}

Itt

a

helyére

b

-t, majd

c

-t írva a

b

, ill.

c

oldallal párhuzamos érintő lemetszette háromszögbe írt kör

ϱ_{2}

, ill.

ϱ_{3}

sugarát kapjuk. Így a négy kör területének összege kiemeléssel, a négyzetek kifejtésében a hasonló szerkezetű tagokat mindjárt egybefogva, továbbalakítással, végül mindent az oldalakkal kifejezve

\begin{matrix} π (ϱ^{2} + ϱ_{1}^{2} + ϱ_{2}^{2} + ϱ_{3}^{2}) = π [4 ϱ^{2} - \frac{2 ϱ^{3}}{t} (a + b + c) + \frac{ϱ^{4}}{t^{2}} (a^{2} + b^{2} + c^{2})] = \\ = \frac{π ϱ^{4}}{t^{2}} (a^{2} + b^{2} + c^{2}) = \frac{π t^{2}}{s^{4}} (a^{2} + b^{2} + c^{2}) = \\ = \frac{π (- a + b + c) (a - b + c) (a + b - c) (a^{2} + b^{2} + c^{2})}{{(a + b + c)}^{3}} \end{matrix}

(ugyanis a szögletes zárójel első két tagjának összege

0

II. megoldás. Tovább is a fenti jelöléseket használva a

ϱ_{1} : ϱ

arányt

H_{1}

és

H

kerületeinek arányából határozzuk meg. Legyenek

H_{1}

új csúcsai

B_{1}

C_{1}

(utóbbi az

A C

-n) és érintse

k

A B

B_{1} C_{1}

C A

B C

egyenest rendre a

C'

A''

B'

A'

pontban. Ekkor a

k

-hoz a

B_{1}

C_{1}

B

C

és

A

pontokból húzott érintőszakaszok egyenlősége alapján

H_{1}

kerülete

\begin{matrix} A B_{1} + B_{1} C_{1} + C_{1} A = (A B_{1} + B_{1} A'') + (A'' C_{1} + C_{1} A) = (A B_{1} + B_{1} C') + \\ + (B' C_{1} + C_{1} A) = A C' + B' A = A B - B C' + A C - B' C = \\ = A B + A C - (B A' + A' C) = c + b - a = 2 (s - a) . \end{matrix}

Így

ϱ_{1} = ϱ (s - a) / s

, és a fentiekhez hasonló rendezési lépésekkel

\begin{matrix} π (ϱ^{2} + ϱ_{1}^{2} + ϱ_{2}^{2} + ϱ_{3}^{2}) = \frac{π ϱ^{2}}{s^{2}} [s^{2} + {(s - a)}^{2} + {(s - b)}^{2} + {(s - c)}^{2}] = \\ = \frac{π t^{2}}{s^{4}} [4 s^{2} - 2 s (a + b + c) + (a^{2} + b^{2} + c^{2})] = \frac{π t^{2}}{s^{4}} (a^{2} + b^{2} + c^{2}) . \end{matrix}

Nagy Sarolta (Budapest, Hámán K. g. IV. o. t.)

Megjegyzés. A

H_{1}

és

H

közti

λ

lineáris nagyítási arányt abból is megkaphatjuk, hogy

k

H_{1}

-re nézve külső érintő kör.

H_{1}

oldalai

a_{1} = λ a

λ b

λ c

, kerületének fele

s_{1} = λ s

, területe pedig

t_{1} = λ^{2} t

, így a külső érintő kör sugarára ismert

ϱ_{a} = t / (s - a)

kifejezés^{$^{*}$} értelemszerű alkalmazásával

\begin{matrix} t / s = ϱ = t_{1} / (s_{1} - a_{1}) = λ t / (s - a), és így λ = (s - a) / s . \end{matrix}

^{$^{*}$}Lásd pl. Kürschák J.‐Hajós Gy.‐Neukomm Gy.‐Surányi J.: Matematikai Versenytételek I, 3. kiadás, Tankönyvkiadó, Budapest, 1965, 36. o.