| Feladat: | 1329. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Fleischer Tamás | ||
| Füzet: | 1965/szeptember, 16 - 17. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Elsőfokú diofantikus egyenletek, Számelrendezések, Logikai feladatok, Oszthatósági feladatok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1964/szeptember: 1329. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen a középső körbe írandó szám és az állandó összeg . Tekintsük az nagy négyzet három során és az oldalfelező pontok alkotta kisebb, négyzet oldalfelezőin álló öt összeg összegét. Ebben minden adott szám egyszer lép fel és további kétszer. Az előírt számok összege , így a következő egyenletet kapjuk
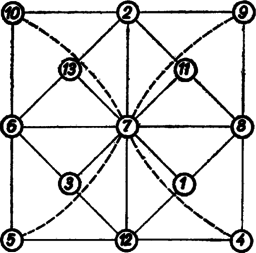 Tekintsük másrészt középső sora, középső oszlopa és jobbra lejtő oldalfelezője összegeinek összegét, és vonjuk ki belőle két balra lejtő oldalának összegét. A különbség egyrészt a szám háromszorosa, másrészt háromszorosának és kétszeresének különbsége, azaz A III. állítással ellentétben felső csúcsára páratlan számot írva, az alsó csúcsra az őt -re kiegészítő számot kell írnunk, ami szintén páratlan. Ha még a bal oldali csúcson is páratlan számmal próbálkozunk, akkor az összeg-követelmény alapján előbb a jobb oldali csúcsra, majd oldalfelező pontjaiba is páratlan számot kell írnunk, mert ha három egész szám összege, továbbá a számok közül is kettő páratlan, akkor a harmadik szám is az. Így kilenc páratlan számot használnánk fel, holott az előírt számok között csak hét van, ilyen elrendezés tehát lehetetlen. Ha viszont bal oldali csúcsán páros számmal próbálkozunk, az összeg-követelmény alapján további öt száma páros lesz, és még két páros szám kell csúcsaiba is, mert a bal és jobb oszlopon csak így lehet páratlan az összeg. Ez sem lehetséges, mert az előírt számok között csak hat páros van. Eszerint a III. állítás igaz, és ha van megoldás, abban a hat páros számból alakítható összegek közül kettőnek a tagjai állnak egy-egy átlóján. Nem lehet a mondott két összeg sem az első kettő, sem az utolsó kettő. Ugyanis az első esetben két szomszédos csúcsára és jut, összegük nagyobb -nél. A második esetben három egymás utáni csúcsán , , áll, és az első kettő között , így pedig a hátra levő -es szám egyik csúcsára sem tehető, mert valamelyik oldalon együtt állna -zel vagy -gyel, és sem , sem nem egészíthető ki -re a hátra levő számokból. A kimaradt , összegpárt írva átlóira és betöltve további számait, a még be nem írt , , , számok csúcsain csak az ábra szerinti elrendezésben felelnek meg, ugyanis a felső soron hiányzó csak alakban, a bal oldalon hiányzó csak alakban állítható elő közülük, ezek közös tagja került bal felső csúcsára. Az ábra elrendezése megfelel az előírásoknak, ide értve a IV. tulajdonságot is. A négyzet szimmetriái miatt a megoldás állásban írható be az ábrába. |