Kezdőlap


Feladat:	1327. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bóta K. , Deák I. , Ferenczi Gy. , Huhn A. , Kiss Katalin , Lovász László , Márki L. , Nagy Klára , Patkós A. , Pelikán J. , Siket Aranka , Simonovits András , Sükösd Cs. , Szabó Mihály , Székely G. , Szemkeő Judit , Treer Mária , Veres F. , Vesztergombi Katalin
Füzet:	1966/január, 12 - 15. oldal		PDF \| MathML
Témakör(ök):	Ábrázoló geometria, Egyenesek egyenlete, Kör egyenlete, Koordináta-geometria, Kör (és részhalmaza), mint mértani hely, Ellipszis, mint mértani hely, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1964/május: 1327. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. $k$ -nak bármely $M$ pontjához szerkeszthető egy $A$ -n átmenő és $S$ -et $M$ -ben érintő $G$ gömb. Valóban, e gömb $P$ középpontjának rajta kell lennie egyrészt az $M$ -ben $S$ -re állított $m$ merőlegesen, másrészt az $A M$ szakasz $S_{1}$ felező merőleges síkján. $S_{1}$ -nek és $m$ -nek mindig van egy határozott közös pontja, hiszen csak úgy lehetnének párhuzamosak, vagy $S_{1}$ úgy mehetne át $m$ -en, ha $S_{1}$ merőleges lenne $S$ -re, ekkor pedig $M$ -mel együtt az $A M$ egyenes és az $A$ pont is $S$ -ben lenne, a feltevéssel ellentétben. $G$ sugara $P$ -nek $M$ -től való távolsága (1. ábra).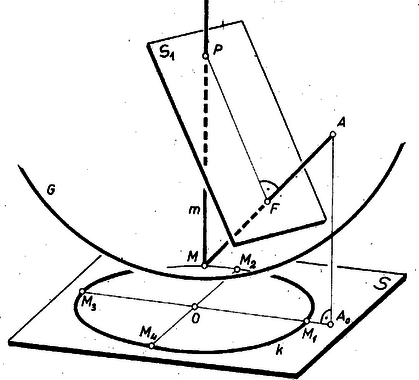

1. ábra

m

egyenes annak a

H

hengerfelületnek egy alkotója, amelynek

S

-beli metszete

k

, és amelynek tengelye merőleges

S

-re; eszerint

P

rajta van

H

-n.
Újabb feltételt kapunk

P

számára, ha bebizonyítjuk a feladat állítását. Ugyanis a gömböknek az állítás szerinti további közös pontját

B

-vel jelölve

A B

minden szóban forgó gömbnek húrja, így

P

mindig az

A B

szakasz felező merőleges síkján,

S_{2}

-n van. Ezek szerint

P

csak

H

és

S_{2}

metszésvonalán,

e

-n lehet. Ismeretes¹, hogy az

e

vonal általában ellipszis, amely lehet kör is, ti. ha

S_{2}

merőleges

H

tengelyére, vagyis párhuzamos

S

-sel, aminek feltétele, hogy

A B

merőleges legyen

S

-re (2. ábr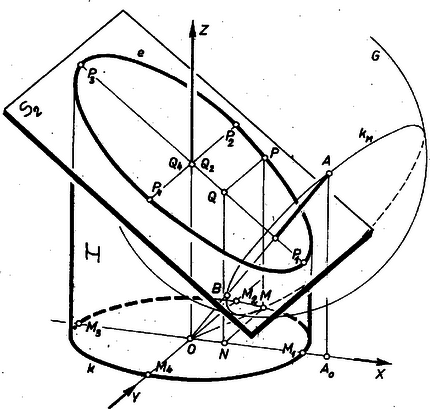a).

2. ábra

Rátérve az állítás bizonyítására, legyen

k

középpontja

O

, sugara

r

. Az

A O M = S_{M}

sík

G

-t egy

k_{M}

körben metszi, és

k_{M}

-nek

M

-beli érintője az

O M

egyenes, mint

S

és

S_{M}

közös egyenese, mert

G

-nek nem lehetnek pontjai

S

két oldalán, és így

k_{M}

-nek sem

O M

két oldalán. Legyen

O A

és

k_{M}

második közös pontja

B

, és alkalmazzuk a körhöz külső pontból húzott szelőre és érintőre ismert tételt

k_{M}

-re és

O

-ra:

\begin{matrix} O A \cdot O B = O M^{2}, innen O B = \frac{O M^{2}}{O A} = \frac{r^{2}}{O A}, \end{matrix}

(1)

állandó (itt

O A \neq 0

, mert

O

S

-ben van,

A

pedig az

S

-en kívül). Eszerint

M

bármely helyzetében

k_{M}

, és vele

G

is, átmegy az

O A

egyenes (1)-gyel meghatározott

B

pontján; az állítás helyes.
Amennyiben

O B = O A

adódik, vagyis

O A = r

, akkor

B

azonos

A

-val, nincs a gömböknek további közös pontja. Ekkor viszont

k_{M}

mindig érinti az

O A

egyenest

A

-ban, és ugyanez áll minden

G

-re, tehát

P

O A

-ra

A

-ban merőlegesen álló síkon van.
Megmutatjuk, hogy az

e

metszésvonal minden

P

pontja hozzátartozik a keresett mértani helyhez: a

P

középpontú,

A

-n átmenő

G

gömb a

k

egy pontjában érinti

S

-et. Az érintési pont csak

P

-nek

S

-en levő

M

vetülete lehet, ez valóban a

k

-n van, hiszen

P

H

henger felületén van; így elég azt belátnunk, hogy

G

átmegy

M

-en. Ekkor a

P M

sugárra

M

-ben merőlegesen álló

O M

egyenes érinti

G

-t. Elég tehát megmutatnunk, hogy

P M = P A

. Mivel

P

S_{2}

síknak is pontja, így az

O B

egyenesen levő

P'

merőleges vetülete² felezi az

A B

szakaszt. Ezért

\begin{matrix} A P^{2} = A P'^{2} + P' P^{2} = A P'^{2} + O P^{2} - O P'^{2} = O P^{2} - (O P' - A P') \cdot (O P' + P' A) = \\ = O P^{2} - (O P' - B P') \cdot (O P' + P' A) = O P^{2} - O B \cdot O A . \end{matrix}

Ebből (1) és

O M = r

folytán

\begin{matrix} A P^{2} = O P^{2} - O B \cdot O A = O P^{2} - r^{2} = O P^{2} - O M^{2} = P M^{2}, \end{matrix}

tehát az

A P

és

P M

távolságok egyenlők,

M

rajta van

G

-n. Ezt akartuk bizonyítani.

Lovász László (Budapest, Fazekas M. Gyak. G.)

II. megoldás. Tovább használjuk az I. megoldás jelöléseit, és felhasználjuk azt a megállapítást, hogy

P

H

hengerfelületen van, valamint a következő síkgeometriai segédtételt: ,,ha az

f

egyenes egy pontja

M

, és a sík egy

f

-en kívüli pontja

A

, akkor az

f

-et

M

-ben érintő és

A

-n átmenő kör sugara

\begin{matrix} ϱ = \frac{M A_{0}^{2} + A_{0} A^{2}}{2 A_{0} A} = \frac{m^{2} + a^{2}}{2 a}, \end{matrix}

(2)

ahol

A_{0}

A

vetülete

f

-re.'' Az állítás a 3. ábra

P M F

és

M A A_{0}

derékszögű háromszögeinek hasonlóságából következik,

F

A M

szakasz felezőpontja, a feltevés miatt

a \neq 0

3. ábra

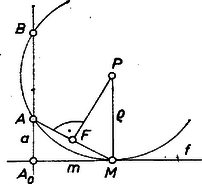Ebből mindjárt adódik, hogy ha a 3. ábra síkja merőleges

S

-re,

S

-sel való metszésvonala

f

, és

A_{0}

azonos

O

-val ‐ vagyis amíg

M

körülfut

k

-n,

A_{0} M

állandó ‐, akkor

ϱ

is állandó, és

P

H

-nak egy az

S

-sel párhuzamos síkkal való metszetén, körön fut körül, hiszen ábránk

H

-nak bármelyik tengelymetszetét megadja. Ebben az esetben

P

-nek bármely az

O A

-n átmenő síkon való vetülete egyenesszakaszt ír le. Továbbá az is adódik, hogy a gömbök második állandó pontja az ábra

B

pontja, ill.

a = m = ϱ

esetén nincs második állandó pont; ekkor viszont mindegyik gömb

A

-ban érinti az

A_{0} A = O A

egyenest.
Megmutatjuk, hogy

P

-nek az

O A

-n átmenő és

S

-re merőleges

S^{*}

síkon levő

Q

vetülete mindig egyenesszakaszt ír le. Ebből már következik, hogy

P

mozgása abban a síkban folyik le, amely merőleges

S^{*}

-ra, és azt a mondott szakasz egyenesében metszi. A szakasz

H

és e sík metszésvonalának a vetülete.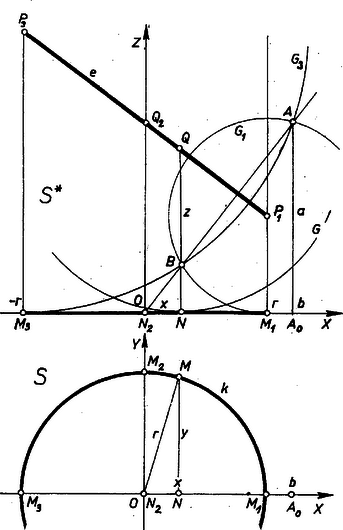

4. ábra

M

és

Q

mozgását egy‐egy derékszögű koordinátarendszerben tekintjük. Legyen ezek közös origója

O

, közös

X

-tengelye az

O A_{0}

egyenes, a másik tengely az

S

-beli rendszerben

Y

, az

S^{*}

-beliben

Z

A_{0}

közös

x

koordinátája

b

, továbbá

M

vetülete

X

-en

N

, így az

M P Q N

négyszög téglalap; legyen végül

O N = x

N M = y

N Q = z

M

pályájának,

k

-nak egyenlete

x^{2} + y^{2} = r^{2}

. (2) felhasználásával

Q

ordinátája (3. és 4. ábra)

\begin{matrix} z = N Q = M P = ϱ = \frac{1}{2 a} (a^{2} + M A_{0}^{2}) = \frac{1}{2 a} [a^{2} + {(b - x)}^{2} + y^{2}] = & (3) \\ = \frac{1}{2 a} [a^{2} + b^{2} - 2 b x + (x^{2} + y^{2})] = \frac{a^{2} + b^{2} + r^{2}}{2 a} - \frac{b}{a} \cdot x . \end{matrix}

Ez az

X Z

koordinátarendszerben valóban egyenes egyenlete. Az egyenesből

Q

k

-ra tekintettel a

- r \leq x \leq r

szakaszt írja le (mégpedig 2-szer).
Az iránytényezőből látható, hogy a talált egyenes ‐ és így

P

pályájának síkja is ‐ merőleges

O A

-ra.

b \neq 0

esetén az egyenes és a sík ferdén hajlik

Z

-hez, ami

H

-nak is tengelye, és így

P

pályája az I. megoldásbeli idézet szerint mindig ellipszis.
A vizsgált gömbök

S^{*}

-ot olyan körben metszik, amelynek középpontja

Q

, és amely átmegy

A

-n. Eszerint a (3) egyenes minden ilyen körnek szimmetriatengelye, tehát minden ilyen kör és minden gömb is átmegy

A

-nak az egyenesre való

B

tükörképen.

B

O A

egyenesen van.

¹Lásd pl. Lőrincz Pál: Ábrázoló geometria a gimn. IV. o. számára, 3. kiadás, Tankönyvkiadó, Bp., 1959. 63. o.

²A 2. ábrán $P'$ beírandó