Feladat: 1325. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Balla Katalin ,  Bódi Z. ,  Bóta K. ,  Deák I. ,  Dévaj Ágnes ,  Ferenczi Gy. ,  Ferenczi M. ,  Horváth J. (Esztergom) ,  Huhn A. ,  Kersner Róbert ,  Kiss Katalin ,  Lovász L. ,  Lovász László ,  Márki L. ,  Mátrai M. ,  Nagy Klára ,  Patkós A. ,  Pelikán J. ,  Racskó P. ,  Siket Aranka ,  Simonovits András ,  Sükösd Cs. ,  Szabó M. ,  Székely G. ,  Szemkeő Judit ,  Sövényházy Mária ,  Treer Mária ,  Veres F. 
Füzet: 1965/május, 207 - 208. oldal  PDF  |  MathML 
Témakör(ök): Ellipszis egyenlete, Hiperbola egyenlete, Diszkusszió, Síkgeometriai szerkesztések, Ellipszis, mint mértani hely, Hiperbola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1964/május: 1325. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az idézett szerkesztést tekinthetjük az (x/a)2+(y/b)2=1 egyenletével adott ellipszis egy pontja ordinátájának szerkesztésére szolgáló eljárásnak is, ha adott a pont abszcisszája, vagy az abszcissza szerkesztésére szolgálónak adott ordináta esetében. Ha ugyanis a használt félegyenest az a, ill. a b sugarú körön levő pontjával jelöljük ki, ezzel megválasztottuk a szerkesztendő pont abszcisszáját, ill. ordinátáját. Hasonlóan kétféle kiindulással értelmezzük az (x/a)2-(y/b)2=1 egyenletű hiperbola pontjai szerkesztésének feladatát.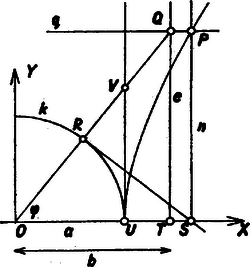
A bemutatandó eljárás abban hasonlít az idézetthez, hogy körzőt csak az első pont szerkesztésében használ, a további pontok szerkesztése derékszögű háromszögű vonalzó-pár használatával végezhető (feltéve, hogy megengedjük párhuzamos, ill. merőleges egyenes rajzolását csúsztatással, ill. átforgatással, amint ez az idézett eljárásban is szokásos). A hiperbola szimmetrikus a két tengelyre, ezért csak I. síknegyedbeli pontokra gondolunk, más szóval nem leszünk tekintettel a hiperbola tengelyeinek mint koordinátatengelyeknek az irányítására.

 
 

Előkészítésül megrajzoljuk az O origó körüli a sugarú k kört (hiperbolánk főkörét) és azt az e egyenest, amely merőleges az X-tengelyre és azt O-tól b távolságban metszi (a b szakasz az a és OF1=c szakaszokból b=c2-a2 alapján megszerkeszthető). Adottnak tekintve a keresett P hiperbolapont y1 ordinátáját, magát a pontot a következő lépésekkel kaphatjuk: 1. e-re az X-tengelybeli pontjától felmérjük y1-et és a Q végponton át q merőlegest állítunk e-re; megrajzoljuk: 2. az OQ félegyenest, legyen a k-val való metszéspontja R; 3. k-nak R-beli érintőjét, legyen az X-tengellyel való metszéspontja S, végül 4. az S-en átmenő és az X-re merőleges egyenest; ennek a q egyenessel való metszéspontja a keresett P.
Megmutatjuk, hogy P-nek OS abszcisszája egyenlő a hiperbola egyenlete alapján az y1 ordinátából számítható
x1=abb2+y12
értékkel. Messe az X-tengely pozitív fele e-t T-ben, k-t U-ban és k-nak U-beli érintője OQ-t V-ben. Ekkor ORS és OUV egybevágó háromszögek, OTQ pedig hasonló hozzájuk, így
OS=OV=OUOT⋅OQ=abOT2+TQ2=abb2+y12=x1,
amit bizonyítani akartunk.
Fordítva, ha P abszcisszája adott, azt az X-tengelyre felmérve kapjuk S-et, ebben n merőlegest állítunk X-re, másrészt S-ből érintőt rajzolunk k-hoz, az érintési pontot O-val összekötő egyenesen megkeressük az e-vel való metszéspontját, végül az ezen át az X-tengellyel párhuzamosan húzott q egyenessel n-ből kimetsszük P-t.
Eljárásainkat tekinthetjük a hiperbola (ill. az ellipszis) és valamelyik tengelyével párhuzamos egyenes metszéspontjai megszerkesztésének is.
 
Lovász László (Budapest, Fazekas M. G.)

 

Megjegyzések. 1. Az eljárás helyességét könnyen igazolhatjuk úgy is, hogy x-et és y-t a QOT=φ szöggel fejezzük ki.
 
Kersner Róbert (Ajka, Bródy I. g. III. o. t.)

 
2. Több dolgozat körzővel vitte át az OV szakaszt OS-be vagy fordítva. Így k helyett az Y-tengelytől a távolságra levő UV egyenes rajzolandó meg. A fenti eljárás OV-nek OS-be való átvitelét ügyesen végzi el a körző mellőzésével, a fordított eljárásban viszont az érintőnek a vonalzó puszta odaillesztésével való megrajzolása a gyakorlatban hibákra vezethet.