Kezdőlap


Feladat:	1321. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bóta Károly , Deák I. , Márki L. , Nagy Klára , Patkós A. , Siket Aranka , Sövényházi Mária , Veres F. , Vesztergombi Katalin
Füzet:	1966/november, 108 - 111. oldal		PDF \| MathML
Témakör(ök):	Számsorozatok, Számelmélet alaptétele, Feladat
Hivatkozás(ok):	Feladatok: 1964/május: 1321. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

1. $a_{0}$ értékét tetszés szerint megválasztva $b_{0}$ értéke csak $a_{0} - a_{1}$ vagy $a_{0} + a_{1}$ lehet (ha ti. $a_{1} > 0$ ; $a_{1} = 0$ esetén pedig $b_{0} = a_{0}$ ), írjuk ezt röviden így: $b_{0} = a_{0} \pm a_{1}$ . Hasonlóan $c_{0} = b_{0} \pm b_{1} = a_{0} \pm a_{1} \pm b_{1}$ , majd $d_{0} = a_{0} \pm a_{1} \pm b_{1} \pm c_{1}$ , végül $a_{0} = d_{0} \pm d_{1} = a_{0} \pm a_{1} \pm b_{1} \pm c_{1} \pm d_{1}$ , vagyis

\begin{matrix} \pm a_{1} \pm b_{1} \pm c_{1} \pm d_{1} = 0. \end{matrix}

(2)

Hagyjuk figyelmen kívül az érdektelen

a_{1} = b_{1} = c_{1} = d_{1} = 0

esetet, így (2) bal oldalán legalább egy szám előtt a

+

jel érvényes a két jel közül, és legalább egy előtt a mínusz jel. Ebből, a mínusz jellel álló számokat a jobb oldalra áttéve,

Q_{0}

létezésének szükséges feltételeként azt kapjuk, hogy

Q_{1}

számai úgy legyenek rendezhetők két csoportba ‐ ti. a

Q_{0}

-on végigmenve növekedést, ill. csökkenést adó változások csoportjára ‐, hogy

α)

mindegyik csoport tartalmazzon legalább egy, a

0

-tól különböző számot, és hogy

β)

a számok összege a két csoportban ugyanannyi legyen.

E feltételek minden lehetséges esetben elegendők is. Ugyanis

α)

miatt a két csoportban vagy

3

és

1

szám áll, vagy

2

‐

2

szám. A második esetben a

2

‐

2

egyenlő jelű szám vagy

2

szomszédos párt alkot, vagy páronként szétválasztják egymást, ezért

β)

a fent idézett megállapításokra tekintettel lényegében

3

különböző típus szerint teljesülhet:

\begin{matrix} a_{1} + b_{1} + c_{1} = d_{1}, & (3') \\ a_{1} + b_{1} = c_{1} + d_{1}, & (3'') \\ a_{1} + c_{1} = b_{1} + d_{1} . & (3''') \end{matrix}

(Ha

Q_{1}

-ben van

0

tag is, a különböző típusok száma kevesebb.) Ekkor egy az (1)-et kielégítő számnégyes rendre:

\begin{matrix} Q'_{0} a_{0}, a_{0} + a_{1}, a_{0} + a_{1} + b_{1}, a_{0} + a_{1} + b_{1} + c_{1}; & (4') \\ Q''_{0} a_{0}, a_{0} + a_{1}, a_{0} + a_{1} + b_{1}, a_{0} + a_{1} + b_{1} - c_{1}; & (4'') \\ Q'''_{0} a_{0}, a_{0} + a_{1}, a_{0} + a_{1} - b_{1}, a_{0} + a_{1} - b_{1} + c_{1}; & (4''') \end{matrix}

ahol

a_{0}

tetszés szerinti egész szám. Most már ezt is mondhatjuk:

Q_{0}

létezéséhez szükséges és elegendő, hogy

Q_{1}

-re a (3

'

)‐(3

'''

) feltételek valamelyike teljesüljön.

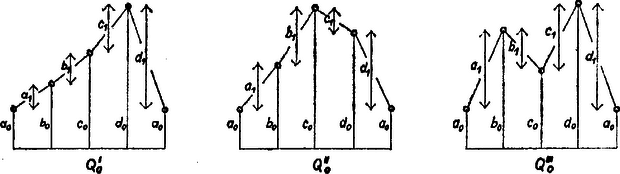
2. Az alábbiakban az

a_{1}

b_{1}

c_{1}

d_{1}

számokat nem valamely

Q_{0}

-ból származtatottnak tekintjük. A számötösön végigmenve a kétszeri növekedés és kétszeri csökkenés lényegében két különböző sorrend szerint léphet föl: nő, nő, fogy, fogy, és nő, fogy, nő, fogy, vagyis

a_{1} \leq b_{1} \leq c_{1} \geq d_{1} \geq a_{1}

, ill.

a_{1} \leq b_{1} \geq c_{1} \leq d_{1} \geq a_{1}

. Éppen ilyen változások adódnak a fenti

Q''_{0}

-ben és

Q'''_{0}

-ben is, ezért az ilyen számnégyesekre fennáll a megfelelő második, ill. harmadik típusú

\begin{matrix} a_{2} + b_{2} = c_{2} + d_{2}, ill. a_{2} + c_{2} = b_{2} + d_{2} \end{matrix}

összefüggés is. Az alábbi táblázatok szerint az első esetben legkésőbb

6

, a másodikban legkésőbb

4

lépés után csupa

0

számnégyesre jutunk, hiszen már

Q''_{6}

mindegyik tagja

a_{5}

, ill.

Q'''_{4}

mindegyik tagja

a_{4}

\begin{matrix} Q "_{1} & a_{1} & ≦ & b_{1} & ≦ & c_{1} & ≧ & d_{1} & ≧ & a_{1} \\ Q "_{2} & a_{2} & b_{2} & c_{2} & d_{2} = a_{2} + b_{2} - c_{2} \\ Q "_{3} & a_{3} & b_{3} & c_{3} & d_{3} = | d_{2} - a_{2} | = | b_{2} - c_{2} | = b_{3} \\ Q "_{4} & a_{4} & b_{4} & c_{4} = | c_{3} - d_{3} | = | c_{3} - b_{3} | = b_{4} & d_{4} = | d_{3} - a_{3} | = | b_{3} - a_{3} | = a_{4} \\ Q "_{5} & a_{5} = | a_{4} - b_{4} | & 0 & a_{5} & 0 \\ Q' "_{1} & a_{1} & ≦ & b_{1} & ≧ & c_{1} & ≦ & d_{1} & ≧ & a_{1} \\ Q' "_{2} & a_{2} & b_{2} & c_{2} & d_{2} = a_{2} - b_{2} + c_{2} \\ Q "_{3} & a_{3} & b_{3} & c_{3} = | c_{2} - d_{2} | = | b_{2} - a_{2} | = a_{3} & d_{3} = | d_{2} - a_{2} | = b_{3} \end{matrix}

(Ez a két sorozat rövidebb is lehet, pl.

c_{2} < a_{2} < b_{2}

esetén

d_{2} > b_{2}

, ezért

a_{3} + c_{3} = b_{2} - a_{2} + d_{2} - c_{2} = 2 (b_{2} - c_{2}) = 2 b_{3} = 2 d_{3}

, ennélfogva

a_{3} - b_{3} = b_{3} - c_{3} = c_{3} - d_{3} = d_{3} - a_{3}

, és már

Q''_{5}

-nek is mindegyik tagja

0

. A

Q_{0} = 1

6

12

5

számnégyesből viszont csak a

6

. lépésben lesz minden tag

0

3. A föltevés szerint

Q_{4}

teljesíti a (3

'

)‐(3

'''

) föltétel valamelyik egyenlőségét (természetesen mindegyik index helyére

4

-est írva), így

Q_{3}

minden esetre képezhető

Q'_{0}

Q''_{0}

és

Q'''_{0}

közül annak a mintájára, amelyikhez tartozó egyenlőség teljesült. Továbbmenve a föltétel egyikének a képezendő

Q_{3}

-ra,

Q_{2}

-re és

Q_{1}

-re is teljesülnie kell; sőt határozottan kimondhatjuk, hogy (3

'

)-nek kell teljesülnie, mert, mint a 2. pontban

Q''_{3}

-ben és

Q'''_{3}

-ben láttuk, egy a (3

''

), ill. (3

'''

) típusú négyesből már egy lépéssel előrehaladva két egyenlő számot tartalmazó négyes adódik, ezt pedig

Q_{4}

-ről nem tehetjük föl. Látni fogjuk, hogy (3

'

) megfelelőjét minden esetben teljesíthetjük

a_{3}

a_{2}

, ill.

a_{1}

alkalmas megválasztásával.

α

) Legyen

Q_{4}

-ben először (3

'

) mintájára

a_{4} + b_{4} + c_{4} = d_{4}

. Ekkor (4

'

) mintájára a tetszés szerinti

a_{3}^{*}

egész számból kiindulva képezett

\begin{matrix} Q'_{3}^{*} a_{3}^{*} a_{3}^{*} + a_{4} a_{3}^{*} + a_{4} + b_{4} a_{3}^{*} + a_{4} + b_{4} + c_{4} \end{matrix}

négyesben mindenesetre a 4. tag a legnagyobb, csak ez lehet egyenlő a többi három összegével:

\begin{matrix} 3 a_{3}^{*} + 2 a_{4} + b_{4} = a_{3}^{*} + a_{4} + b_{4} + c_{4}, amiből \\ a_{3}^{*} = \frac{c_{4} - a_{4}}{2} . \end{matrix}

Törtek nélkül számolhatunk, ha

Q_{4}

tagjainak páros voltát felhasználva minden számunk felét a megfelelő nagy betűvel jelöljük (az indexet változatlanul kiírva). Így

\begin{matrix} a_{3}^{*} = C_{4} - A_{4} és \end{matrix}

\begin{matrix} Q'_{3} a_{3} & = - A_{4} + C_{4}, b_{3} = A_{4} + C_{4}, c_{3} = A_{4} + 2 B_{4} + C_{4}, & (5) \\ d_{3} & = A_{4} + 2 B_{4} + 3 C_{4} . \end{matrix}

a_{3} \geq 0

csak

c_{4} \leq a_{4}

esetén teljesül, ez azonban ‐ ha nem így volna ‐ elérhető azzal, hogy

Q_{4}

számait

c_{4}

-től kezdve és visszafelé haladva vesszük sorba (vagyis a többiek összegével egyenlő

d_{4}

kisebbik szomszédját vesszük

a_{4}

-nek).
Ezzel olyan képletcsoportot kaptunk a számnégyes-sorozat visszafelé

1

lépéssel való meghosszabbítására, amelynek eredménye mintegy készen áll egy újabb ilyen meghosszabbításra, hiszen

Q'_{3}

-ben ugyanaz a feltétel teljesül, mint

Q_{4}

-ben:

a_{3} + b_{3} + c_{3} = d_{3}

. Eszerint (5)-ben minden indexet

1

-gyel csökkentve

Q'_{2}

-nek pl. a

3

. tagja

\begin{matrix} c_{2} = A_{3} + 2 B_{3} + C_{3} = \frac{a_{3} + c_{3}}{2} + b_{3} = (B_{4} + C_{4}) + (A_{4} + C_{4}) = A_{4} + B_{4} + 2 C_{4}, \end{matrix}

és hasonló számításokkal a teljes számnégyes:

\begin{matrix} Q'_{2} a_{2} = A_{4} + B_{4}, b_{2} = B_{4} + C_{4}, c_{2} = A_{4} + B_{4} + 2 C_{4}, d_{2} = 2 A_{4} + 3 B_{4} + 3 C_{4} . \end{matrix}

(6)

Az indexek csökkentésével

Q'_{3}

mintájára képezzük

Q'_{1}

-et, abból pedig (4

'

) alapján

Q'_{0}

-t (abban ugyanis már nem kell teljesülnie (3

'

)-nek). Pl.

\begin{matrix} d_{1} = A_{2} + 2 B_{2} + 3 C_{2} = \frac{1}{2} (a_{2} + 2 b_{2} + 3 c_{2}) = 2 A_{4} + 3 B_{4} + 4 C_{4}, és \end{matrix}

\begin{matrix} Q'_{1} & a_{1} & = C_{4}, & b_{1} & = A_{4} + B_{4} + C_{4}, & c_{1} & = A_{4} + 2 B_{4} + 2 C_{4}, & d_{1} & = 2 A_{4} + 3 B_{4} + 4 C_{4} . & (7) \\ Q'_{0} & a_{0}, & b_{0} & = a_{0} + C_{4}, & c_{0} & = a_{0} + A_{4} + B_{4} + 2 C_{4}, & d_{0} & = a_{0} + 2 A_{4} + 3 B_{4} + 4 C_{4}, & (8) \end{matrix}

ahol

a_{0}

tetszés szerinti egész szám. Pl. a

Q_{4} = 6

14

22

42

négyes kiadódik

Q_{0} = a_{0}

a_{0} + 11

a_{0} + 32

a_{0} + 71

-ből.

β

) Ha az előírt

Q_{4}

-ben a (3

''

) típusú

b_{4} + c_{4} = d_{4} + a_{4}

feltétel teljesül, akkor a (4

''

) mintájára képezett

\begin{matrix} N''^{*} a_{3}^{*}, b_{3}^{*} = a_{3}^{*} - a_{4}, c_{3}^{*} = a_{3}^{*} - a_{4} + b_{4}, d_{3}^{*} = a_{3}^{*} - a_{4} + b_{4} + c_{4} \end{matrix}

számnégyesben (a továbbiakban

Q

betűk helyett

N

-eket használunk, így elkerüljük a 2. részbeli jelölések más jelentéssel való megismétlését)

d_{3}^{*}

a legnagyobb szám, ezért a (3

'

) típusú föltétel:

\begin{matrix} a_{3}^{*} + b_{3}^{*} + c_{3}^{*} = d_{3}^{*}, innen a_{3}^{*} = (a_{4} + c_{4}) / 2 = A_{4} + C_{4}, és az \\ N''_{3} a_{3} = A_{4} + C_{4}, b_{3} = - A_{4} + C_{4}, c_{3} = - A_{4} + 2 B_{4} + C_{4}, d_{3} = - A_{4} + 2 B_{4} + 3 C_{4} \end{matrix}

alkalmas a számnégyes-sorozat visszafelé való újabb meghosszabbítására (itt is elérhető

b_{3} \geq 0

). Felírhatjuk mindjárt az

N''_{1}

négyest, ugyanis a (6) képletcsoport alkalmas a sorozat visszafelé

2

lépéssel való olyan meghosszabbítására, amelynek eredménye ismét készen áll újabb meghosszabbításra ‐ hacsak az ottani

c_{4} \geq a_{4}

-nek megfelelően itt

c_{3} \geq a_{3}

, azaz

b_{4} \geq a_{4}

. A számítást részletesen

N''_{1}

második tagjára mutatjuk be; (6)-ot alkalmazzuk az indexek csökkentésével

N''_{3}

-ra:

\begin{matrix} b_{1} = B_{3} + C_{3} = \frac{b_{3}}{2} + \frac{c_{3}}{2} = \frac{- A_{4} + C_{4}}{2} + \frac{- A_{4} + 2 B_{4} + C_{4}}{2} = - A_{4} + B_{4} + C_{4}, \end{matrix}

a teljes négyes pedig

\begin{matrix} N''_{1} a_{1} = C_{4}, b_{1} = - A_{4} + B_{4} + C_{4}, c_{1} = - A_{4} + 2 B_{4} + 2 C_{4}, \\ d_{1} = - 2 A_{4} + 3 B_{4} + 4 C_{4} \end{matrix}

Ebből pedig (4

'

) alapján

\begin{matrix} N''_{0} a_{0}, a_{0} + C_{4}, a_{0} - A_{4} + B_{4} + 2 C_{4}, a_{0} - 2 A_{4} + 3 B_{4} + 4 C_{4} . \end{matrix}

(9)

Pl.

Q_{0} = 6

8

12

14

kiadódik ebből:

N''_{0} = a_{0}

a_{0} + 6

a_{0} + 13

a_{0} + 30

γ

) Végül ha

Q_{4}

-ben (3

'''

)-nek megfelelően

a_{4} + c_{4} = b_{4} + d_{4}

, és itt

a_{4} \leq c_{4}

, továbbá

a_{3} \leq c_{3}

, azaz

a_{4} \geq b_{4}

, akkor a

β

) esethez hasonlóan (4

'''

), (3

'

), (6),végül (4

'

) fölhasználásával

\begin{matrix} \begin{matrix} N'''_{3} & - A_{4} + C_{4}, & A_{4} + C_{4}, & A_{4} - 2 B_{4} + C_{4}, & A_{4} - 2 B_{4} + 3 C_{4}; \\ N'''_{1} & C_{4}, & A_{4} - B_{4} + C_{4} (= D_{4}), & A_{4} - 2 B_{4} + 2 C_{4}, & 2 A_{4} - 3 B_{4} + 4 C_{4}; \\ N'''_{0} & a_{0}, & a_{0} + C_{4}, & a_{0} + A_{4} - B_{4} + 2 C_{4}, & a_{0} + 2 A_{4} - 3 B_{4} + 4 C_{4} . & (10) \end{matrix} \end{matrix}

Pl.

Q_{4} = 12

6

14

20

kiadódik az

N'''_{0} = a_{0}

a_{0} + 7

a_{0} + 17

a_{0} + 31

számnégyesből.

4. Eddigi eredményeink alapján gyorsan megkaphatjuk egy a

Q_{16} = 32

32

32

32

négyesre vezető számnégyes-sorozat

Q_{0}

kezdő számnégyesét, pl. az alábbi lépésekben.

Q_{16}

-ban teljesül a (3

'''

) típusú követelmény, ebből (10) alapján képezzük

Q_{12}

-t, és úgy határozzuk meg

a_{12}

-t, hogy teljesüljön (3

'

\begin{matrix} Q_{12} a_{12}, a_{12} + 16, a_{0} + 32, a_{12} + 48; a_{12} = 0 \end{matrix}

(megengedett érték). Innen egymás után (7), (7), (6), végül (8) alkalmazásával,

a_{0} = 0

választásával

\begin{matrix} Q_{9} : 16, 24, 48, 88; Q_{6} : 24, 44, 80, 148; Q_{4} : 34, 62, 114, 210; \\ Q_{0} = 0, 57, 162, 355. \end{matrix}

Bóta Károly (Budapest, Fazekas M. Gyak. G.)

Megjegyzés. A fentiek azt is adták, hogy lehet képezni olyan számnégyest, amelyből kiindulva tetszés szerint előírt számú lépésben kapjuk először a

0

0

0

0

számnégyest (

Q_{0}

esetében

17

lépés). Ugyanis

Q_{0}

számait

a_{0} = 68

-cal emelve tovább hosszabbítható visszafelé, és bár így törtek lépnek föl, ezek nevezőjének legkisebb közös többszörösével szorozva egész számnégyest kapunk. (Nevezőként csak

2

-nek pozitív egész kitevős hatványai lépnek fel.)
Ez a meggondolás viszont azt is adja, hogy egész számokhoz ragaszkodva a sorozat mindig véges számú számnégyesből áll. (Számnégyesek helyett számhármasokat véve, a sorozat lehet végtelen hosszú is, pl. a

0

1

1

számhármast a

3

. lépésben, a

0

0

0

1

1

számötöst a

15

. lépésben visszakapjuk.)