| Feladat: | 1320. matematika feladat | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bóta K. , Deák I. , Ferenczi M. , Hoffer Anna , Horányi S. , Huhn András , Kersner R. , Kövér Á. , Lux I. , Márki L. , Simonovits András , Szántó O. , Szemkeő Judit , Szendrődi Annamária , Szép A. , Treer Mária , Veres F. | ||
| Füzet: | 1966/március, 101 - 104. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Térbeli ponthalmazok távolsága, Térelemek és részeik, Térgeometriai számítások trigonometria nélkül, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1964/április: 1320. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A kérdés ,,elég'' szava minden egyes értékhez a legkisebb olyan átmérő meghatározását kívánja, amelyre a átmérőjű gömb felületén még elhelyezhető pont úgy, hogy ne zavarják egymást. A megadandó értékek közül csak néhányról fogjuk megmutatni, hogy azok valóban a legkisebb megfelelő értékek, a további esetekben csak néhány kínálkozó pontelrendezés közül választjuk ki a legkisebb gömbön elhelyezhetőt, túl terjedelmes bizonyítások és diszkussziók elkerülése végett. 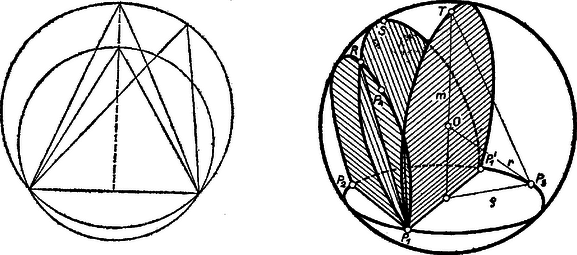 . Két pont az 1 átmérőjű gömbön 1 távolságra van, ha átellenes pontok, kisebb gömbön pedig mindig 1-nél kisebb távolságra van, tehát . Ha a 4 pont nincs egy síkban, akkor jelöljük valamelyik 3 pont, mondjuk , , síkja által kimetszett kör sugarát -val. A pont távolsága és valamelyikétől nem nagyobb, mint a , , -en átmenő körben a -re merőleges átmérőn a húrtól távolabbi végpont, távolsága. -nek től való távolsága ismét nem nagyobb, mint a en, -en és a -gyel a körben átellenes ponton átmenő körben a -re merőleges átmérő távolabbi végpontjának távolsága -től; ez viszont nem nagyobb, mint a főkörben a -re merőleges átmérő távolabbi végpontjának távolsága -től (vagy a kör bármely pontjától). Ha tehát , , , nem zavarja egymást, akkor , , , sem. Az ezeken átmenő gömb átmérője, adott mellett, akkor a legkisebb, ha távolsága a másik három ponttól legkisebb, tehát 1. Ekkor, a gömb sugarát -rel jelölve, távolságát pedig a sugarú körtől -mel: Ez akkor a legkisebb, ha a lehető legkisebb. Mivel a körbe háromszög írható 1-nél nem kisebb oldalakkal, így az esetből tudjuk, hogy minimális értéke . Így minimális értéke (Ez valóban kisebb az első esetben adódott értéknél.) A négy pont ekkor egy szabályos tetraéder négy csúcsa. 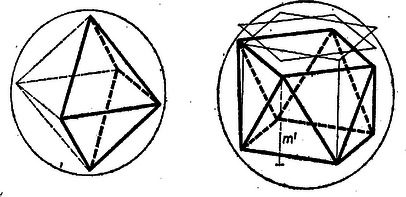 -ra áttérve ‐ az eddigiekkel ellentétben ‐ nem növekszik a legkisebb átmérő értéke, mert az előbb említett gúla csúcsát az alapnégyzetre tükrözve a átmérőjű gömbbe írt szabályos oktaédert kapunk, csupa egységnyi éllel. 5 vagy 6 pontot helyezve egy síkba, nagyobb (, ill. 2) átmérőjű gömb adódik. Így Ennél kisebb átmérő nem adódhat, hiszen a 6 pont közül bármelyik 5 sem zavarja egymást, tehát . esetén elsőnek az egységnyi élű kocka csúcsaiba ültetjük pontjainkat, ekkor az átmérő ; azonban kisebb átmérőjű elrendezést kapunk a felső 4 pont -os elforgatásával és az alsó négyhez való közelítésével olyan távolságra, hogy a megnyúlt oldalélek újra egységnyire csökkenjenek. Ekkor az oldalél egyik végpontjából a másikba az eredeti kockaélekkel párhuzamos , , hosszúságú elmozdulásokkal juthatunk el, így Pythagoras tétele alapján Treer Mária (Budapest, Kaffka M. G.). |