Kezdőlap


Feladat:	1318. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bódi Z. , Bojtár János , Bóta K. , Bulkai L. , Csiszár Z. , Csörnyei Z. , Czina F. , Deák I. , Dévaj Ágnes , Ferenczi Gy. , Hegedűs Aletta , Hirka A. , Horányi S. , Hortobágyi J. , Horváth J. (Bp., Bláthy t.) , Huhn A. , Kerényi I. , Kersner R. , Kiss Katalin , Körner J. , Kövér Á. , Lehel Cs. , Lőrincz I. , Lovász L. , Lugosi P. , Lux I. , Márki L. , Mátrai M. , Nagy Klára , Palotás Á. , Patkós A. , Pelikán J. , Siket Aranka , Simonovits András , Sófalvi M. , Surányi L. , Sükösd Cs. , Szabó M. , Székely G. , Szép A. , Sövényházy Mária , Treer Mária , Veres F. , Vesztergombi Katalin
Füzet:	1965/április, 166. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Súlyvonal, Magasságvonal, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1964/április: 1318. matematika feladat

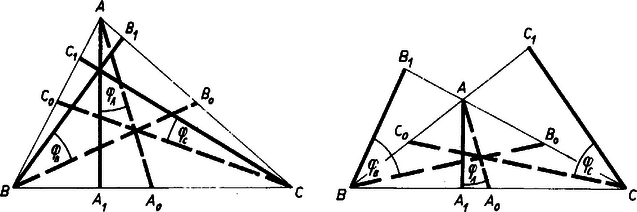
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a $B C$ , $C A$ , $A B$ oldal felezőpontja rendre $A_{0}$ , $B_{0}$ , $C_{0}$ és az $A$ , $B$ , $C$ -ből húzott magasság talppontja rendre $A_{1}$ , $B_{1}$ , $C_{1}$ . Ekkor a bizonyítandó állítás így írható:

\begin{matrix} \frac{A_{1} A_{0}}{A_{1} A} + \frac{C_{1} C_{0}}{C_{1} C} - \frac{B_{1} B_{0}}{B_{1} B} = 0. \end{matrix}

(1)

Egyenlő szárú háromszögre

b

egyenlő

a

-val vagy

c

-vel, így

φ_{B}

φ_{A}

-val vagy

φ_{C}

-vel, és a másik

0

; tehát az állítás igaz. A továbbiakban feltesszük, hogy

a > b > c

, és így

α > β > γ

. A pontok sorrendje a

B C

oldalon

B

-től

C

felé

A_{1}

A_{0}

, ‐ mert a

B C

-re

A_{0}

-ban emelt merőlegesnek

A

azon az oldalán van, mint

B

‐, a

C A

oldalegyenesen

C

B_{0}

B_{1}

, a

B A

oldalegyenesen

B

C_{0}

C_{1}

. Az utóbbi két oldalegyenesen az

A

csúcs

α < 90^{\circ}

esetén a magasságtalppont után következik,

α > 90^{\circ}

esetén közvetlenül előtte,

α = 90^{\circ}

esetén pedig egybeesik vele.

α < 90^{\circ}

esetén az

A B B_{1}

és

A C C_{1}

hasonló derékszögű háromszögekből

\begin{matrix} (ctg α =) \frac{A B_{1}}{B_{1} B} = \frac{A C_{1}}{C_{1} C}, azaz \frac{A B_{0} - B_{1} B_{0}}{B_{1} B} = \frac{A C_{0} - C_{1} C_{0}}{C_{1} C} . \end{matrix}

(2)

Az átalakítás

α ≧ 90^{\circ}

esetén is érvényes, ha az

A C

, ill.

A B

egyenesen irányítást vezetünk be, és pozitívnak vesszük az

A

-tól

C

, ill.

B

felé mutató irányt. Hasonlóan a

B C C_{1}

és

B A A_{1}

, valamint a

C A A_{1}

és

C B B_{1}

hasonló háromszögpárokból

\begin{matrix} (ctg β =) \frac{B C_{1}}{C_{1} C} = \frac{B A_{1}}{A_{1} A}, azaz \frac{B C_{0} + C_{0} C_{1}}{C_{1} C} = \frac{B A_{0} - A_{1} A_{0}}{A_{1} A}, \end{matrix}

(3)

\begin{matrix} (ctg γ =) \frac{C A_{1}}{A_{1} A} = \frac{C B_{1}}{B_{1} B}, azaz \frac{C A_{0} + A_{0} A_{1}}{A_{1} A} = \frac{C B_{0} + B_{0} B_{1}}{B_{1} B} . \end{matrix}

(4)

Most már (2)‐(4) átalakításaiban a bal és a jobb oldalakat összeadva a kapott egyenlőségből

A B_{0} = B_{0} C

B C_{0} = C_{0} A

és

C A_{0} = A_{0} B

figyelembevételével és rendezéssel (1)-et kapjuk.
Bojtár János (Budapest, Lékai J. 12. évf. isk. IV. g. o. t.)