Kezdőlap


Feladat:	1317. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bódi Z. , Bóta K. , Deák I. , Ferenczi Gy. , Ferenczi M. , Horányi S. , Huhn A. , Kalmár Tibor , Kiss Katalin , Lehel Cs. , Lovász L. , Lux I. , Márki L. , Mátrai M. , Nagy Klára , Palotás Á. , Pelikán József , Siket Aranka , Szabó M. , Székely G. , Sövényházy Mária , Veres F. , Vesztergombi Katalin
Füzet:	1965/november, 130 - 133. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Sokszögek súlypontjának koordinátái, Egyenesek egyenlete, Paralelogrammák, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1964/április: 1317. matematika feladat

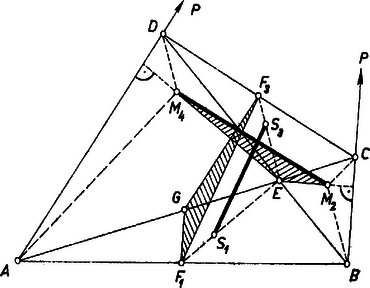
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A B E = H_{1}$ , $B C E = H_{2}$ , $C D E = H_{3}$ , $D A E = H_{4}$ háromszög magasságpontja és súlypontja rendre $M_{i}$ , ill. $S_{i}$ $(i = 1$ , $2$ , $3$ , $4)$ ; (1. ábra). Megmutatjuk, hogy az $M_{i}$ pontok ‐ és az $S_{i}$ -k is ‐ egy-egy paralelogramma csúcsai, azok egymáshoz azonos körüljárással hasonlók, és megfelelő oldalaik merőlegesek egymásra. Ebből már következik, hogy egyiket $90^{\circ}$ -kal elforgatva a másikkal hasonló helyzetbe jut. Végül megmutatjuk, hogy a kérdéses $M_{1} M_{3}$ és $S_{2} S_{4}$ szakaszok a paralelogrammák megfelelő átlói, tehát ezek is merőlegesek. ‐ Ha az $A C$ és $B D$ átlók merőlegesek, akkor mindegyik $M_{i}$ azonos $E$ -vel, az állítás tárgytalan, ezért feltesszük, hogy az átlók nem merőlegesek, és a betűzést úgy választjuk, hogy $A E B = ε$ hegyesszög.

H_{1}

-nek és

H_{2}

-nek

B

csúcsa és a vele szemben levő oldalának

A C

egyenese közös, ezért

S_{1} S_{2}

párhuzamos

A C

-vel, hiszen

S_{1}

is,

S_{2}

is harmad akkora távolságban van

A C

-tól, mint

B

, ugyanazon az oldalon. Ugyanígy

S_{3} S_{4} ∥ A C

, tehát

S_{3} S_{4} ∥ S_{1} S_{2}

, továbbá

S_{1} S_{4} ∥ B D ∥ S_{2} S_{3}

, az

S_{1} S_{2} S_{3} S_{4} = S

négyszög valóban paralelogramma.

S

oldalainak hossza

S_{1} S_{2} = A C / 3

S_{1} S_{4} = B D / 3

M_{1}

és

M_{2}

B

-ből

A C

-re bocsátott merőleges pontjai, ezért

M_{1} M_{2}

merőleges

A C

-re, ugyanígy

M_{3} M_{4}

is, így

M_{1} M_{2} ∥ M_{3} M_{4}

, hasonlóan

M_{1} M_{4} ⊥ B D ⊥ M_{2} M_{3}

, tehát az

M_{2} M_{1} M_{4} M_{3} = M

négyszög paralelogramma. Továbbá

M

és

S

két-két oldala merőleges:

M_{2} M_{1}

és

M_{4} M_{3}

merőleges

S_{1} S_{2}

-re,

M_{3} M_{2}

és

M_{1} M_{4}

merőleges

S_{2} S_{3}

-ra, így a két paralelogramma szögei egyenlők, mert merőleges szárú szögek vagy egyenlők, vagy kiegészítő szögek, és egy paralelogramma szögei ugyancsak kiegészítő szögek.
Legyen az

A

B

C

D

csúcs vetülete a vele szemben levő átlón rendre

A'

B'

C'

D'

; ekkor

M_{1} M_{2} = A' C' / sin ε

, másrészt

A' C' = A C cos ε

, ezért

M_{1} M_{2} = A C ctg ε

, hasonlóan

M_{2} M_{3} = B D ctg ε

, így az oldalak aránya

\begin{matrix} M_{3} M_{2} : M_{2} M_{1} = B D : A C = S_{4} S_{1} : S_{1} S_{2} . \end{matrix}

Ebből és a szögek egyenlőségéből következik

M

és

S

hasonlósága, mert véve egy-egy egyenlő szögüket, az ennek csúcsával szemben fekvő átló

M

-et is,

S

-et is páronként hasonló háromszögekre bontja, továbbá körüljárásuk egyező volta, mert a figyelembe vett egyenlő szögek merőleges szárain vannak az egymással arányos oldalszakaszok.
Hátra van még annak belátása, hogy az

M_{1}

csúcsnak

S_{2}

felel meg, ezeknél vannak tompaszögek. Mindegyik

S_{i}

E

pont körüli négy szögtartomány közül abban van, amelyikben a megfelelő

H_{i}

, mert a súlypont mindig a háromszög belsejében van, így

S_{1} S_{2} S_{3} ∢ = C E B ∢ = 180^{\circ} - ε

, váltószögek.

M_{2}

H_{4}

-et,

M_{4}

pedig a

H_{2}

-t tartalmazó szögtartomány pontja, mert tompaszögű háromszög magasságpontja a tompaszög csúcsából induló magasságnak a csúcson túli meghosszabbításán van.

M_{1}

viszont a

H_{1}

-et tartalmazó szögtartományban van, vagy a határán, amíg csak az

E A B

és

E B A

szögek egyike sem tompaszög, ekkor az

M_{2} M_{1} M_{4}

és

A E B

szögek összege

180^{\circ}

M_{1}

-nél tompaszög van, amint állítottuk. ^{$^{*}$}
Ha pedig

H_{1}

-ben, mondjuk

A

-nál, tompaszög van (2. ábra), akkor

M_{1}

is az

A E D

szögtartomány pontja, de

B

-höz közelebb van, mint

M_{2}

, mert a

B D

átlón levő

A'

C'

vetületeik közül

A'

van közelebb

B

-höz, hiszen

B E A

hegyesszög,

B E C

pedig tompaszög. Így

A M_{1} B ∢ = A' E A ∢ = ε

, és

M_{2} M_{1} A' ∢ = M_{2} M_{1} M_{4} ∢

ennek kiegészítő szöge.
Mindezekből ‐ mint láttuk ‐ következik az állítás.

Pelikán József (Bp., Fazekas M. G.) dolgozatából, kiegészítésekkel.

II. megoldás. A feladat szövegének megfelelően konvex négyszögre szorítkozunk, feltesszük továbbá ismét, hogy az átlók nem merőlegesek. Jelöljük

A B

A C

és

D C

felezőpontját rendre

F_{1}

G

F_{3}

-mal (3. ábra), egyébként az I. megoldás jelöléseit használjuk.

3. ábra

S_{1}

és

S_{3}

E F_{1}

E F_{3}

szakaszok

E

-től távolabbi harmadoló pontja, így

S_{1} S_{3} ∥ F_{1} F_{3}

. Azt kell megmutatnunk, hogy

M_{2} M_{4}

merőleges erre a középvonalra. Ez világos, ha

A D ∥ B C

. Tegyük fel, hogy ez nem áll. A betűzést válasszuk úgy, hogy a két oldal

D

-n, ill.

C

-n túli meghosszabbítása messe egymást egy

P

pontban.
Megmutatjuk, hogy

M_{2} E M_{4} Δ \sim F_{1} G F_{3} Δ

, a két háromszög egyező körüljárású és egymáshoz képest

90^{\circ}

-kal vannak elforgatva. Ebből következik, hogy

M_{2} M_{4}

és

F_{1} F_{3}

oldalaik merőlegesek.

F_{1} G

és

G F_{3}

, mint az

A B C Δ

és

C A D Δ

középvonala, párhuzamos és egyirányú

B C

-vel, ill.

A D

-vel, és fele akkora, mint a megfelelő oldal. Így

F_{1} G F_{3} ∢ = 180^{\circ} - B P A ∢

, és az

A B C D

és

F_{1} G F_{3}

körüljárás ellentétes.
Ha a

B E C ∢

(és így

D E A ∢

is) hegyesszög, akkor

M_{2}

és

M_{4}

E

-ből a szemközti oldal felé haladó félegyenesen van, ha pedig a mondott szög tompaszög, akkor mindkét magasságpont az ellentétes irányú félegyenesen van, így

M_{2} E M_{4} ∢ = 180^{\circ} - B P A ∢

, és az

M_{2} E M_{4}

körüljárási irány ellentétes a

B P A

, és vele együtt az

A B C D

körüljárási iránnyal.
Az oldalak arányának megállapítására azt fogjuk felhasználni, hogy egy

T U V

háromszög magasságpontját

Z

-vel jelölve

U Z = T V | ctg T U V ∢ |

. (Ez belátható a szinusz-tételt alkalmazva pl. az

U V Z

és

T U V

háromszögre, vagy azt használva fel, hogy a magasságpontnak bármelyik oldalra vonatkozó tükörképe a háromszög köré írt körön van.) Ennek felhasználásával

\begin{matrix} \frac{M_{2} E}{E M_{4}} = \frac{B C | ctg B E C ∢ |}{A D | ctg A E D ∢ |} = \frac{B C}{A D} = \frac{F_{1} G}{G F_{3}} . \end{matrix}

Ezek szerint az

M_{2} E M_{4}

és

F_{1} G F_{3}

háromszögben az

E

-nél, ill.

G

-nél levő szög egyenlő, és egyenlő a szöget bezáró oldalak aránya, tehát a két háromszög hasonló, továbbá körüljárásuk is megegyező (ellentétes a négyszög körüljárásával). Ezzel állításainkat igazoltuk.

Megjegyzés. A bemutatott ötletes megoldás utal egyben arra is, hogy a hasonlóság belátása óvatosságot igényel: nem elegendő arra hivatkozni, hogy az

E M_{2}

E M_{4}

magasságok merőlegesek a megfelelő oldalakra. Ez fennállna arra a háromszögre is, amely pl.

F_{1}

-nek a két átló felezőpontjaival való összekötésével keletkeznék, az

F_{1}

-ből induló oldalak aránya is

B C : A D

volna, mégsem kapnánk

M_{2} E M_{4}

-hez hasonló háromszöget. Másrészt a bizonyítandó merőlegességre való következtetéshez szükséges volt a körüljárási irány megvizsgálása is. Ezeken a pontokon egy beküldött megoldás sem volt kifogástalan.
További elemzést igényelne annak belátása, hogy ez a gondolatmenet hogyan szolgáltatja a bizonyítandó állítást, ha a négyszög nem konvex.

III. megoldás. A pont körre vonatkozó hatványa fogalmának, valamint a két kör hatványvonalára vonatkozó tételnek^{$^{*}$} felhasználásával az állítást így bizonyíthatjuk. Tekintsük az

A B

B C

C D

D A

oldal, mint átmérő fölé írt

k_{i}

Thalész-kört, legyen a középpont rendre

F_{i}

(

i = 1

2

3

4

; 1. ábra). Az I. megoldásban szereplő

A'

B'

C'

D'

pontok mindegyikén kettő megy át e körök közül. ─

M_{1} A

és

M_{1} B

k_{1}

kör két szelője, ezért

\begin{matrix} M_{1} A \cdot M_{1} A' = M_{1} B \cdot M_{1} B', \end{matrix}

a két oldal közös értéke az

M_{1}

pont hatványa a

k_{1}

körre. A bal oldal egyszersmind

M_{1}

hatványa

k_{4}

-re, a jobb oldal pedig

k_{2}

-re, egyenlőségük miatt

M_{1}

rajta van

k_{4}

és

k_{2}

hatványvonalán. Hasonlóan

k_{3}

-ból

\begin{matrix} M_{3} C \cdot M_{3} C' = M_{3} D \cdot M_{3} D', \end{matrix}

eszerint

M_{3}

-nak is egyenlő a

k_{4}

-re és

k_{2}

-re vonatkozó hatványa, ennélfogva az

M_{1} M_{3}

egyenes a

k_{4}

k_{2}

körpár hatványvonala, és így merőleges e körök centrálisára, az

F_{4} F_{2}

egyenesre. ‐ A II. megoldásban láttuk, hogy

F_{4} F_{2} ∥ S_{4} S_{2}

, így valóban

M_{1} M_{3} ⊥ S_{2} S_{4}

Megjegyzés. Ez a megoldás mutatja, hogy az állítás konkáv és hurkolt négyszögre is érvényes.

IV. megoldás. Helyezzünk derékszögű koordinátarendszert az ábrára

E

-vel mint origóval, legyen az

X

-tengely az

A C

egyenes,

tg ε = m

, és a csúcsok koordinátái:

A (a,0)

C (c,0)

B (b, m b)

D (d, m d)

, ahol

a \neq c

, és

b \neq d

, mert

A

és

C

, valamint

B

és

D

különböző pontok, továbbá

m \neq 0

, véges szám, mert

ε \neq 90^{\circ}

.
A

H_{1}

háromszög

B

-ből és

A

-ból húzott magasságának

\begin{matrix} x = b, ill. y = - \frac{1}{m} (x - a) \end{matrix}

egyenletéből

M_{1}

metszéspontjuk koordinátái:

M_{1} (b, (a - b) / m)

. Hasonlóan,

a

és

b

helyére

c

-t, ill.

d

-t írva

M_{3} (d, (c - d) / m)

, ezek szerint az

M_{1} M_{3}

egyenes iránytényezője

\begin{matrix} \frac{a - b - c + d}{m (b - d)} . \end{matrix}

(1)

H_{2}

és

H_{4}

súlypontjának koordinátái:

S_{2} [(b + c) / 3, m b / 3]

, ill.

S_{4} [(a + d) / 3, m d / 3]

, ezekből az

S_{2} S_{4}

egyenes iránytényezője

\begin{matrix} \frac{m (d - b)}{a + d - b - c}, \end{matrix}

ami (1) reciprokának

(- 1)

-szerese. Ezzel az állítást bebizonyítottuk.
Amennyiben (1) értéke

0

, vagyis

M_{1} M_{3}

párhuzamos az

X

-tengellyel, akkor a két ordináta egyenlőségéből

a - b = c - d

, és így

a + d = b + c

, vagyis

S_{2}

és

S_{4}

abszcisszái egyenlők,

S_{2} S_{4}

merőleges az

X

-tengelyre, tehát az állítás ekkor is igaz.

Kalmár Tibor (Esztergom, Temesvári Pelbárt g.)

Megjegyzés. Ez a bizonyítás is mutatja, hogy az állítás nem konvex négyszögre is igaz. Ha ugyanis pl.

a

b

c

pozitívok, és

d

negatív, akkor az

A B C D

négyszög konkáv, ha pedig a

d

is pozitív, akkor hurkolt.

^{$^{*}$}Ebben az esetben könnyű látni, hogy az

M_{1} M_{2} M_{3} M_{4}

körüljárás ellentétes

S_{1} S_{2} S_{3} S_{4}

-gyel; ez a további esetekben is belátható.

^{$^{*}$}Lásd pl. Gallai T.‐Hódi E.‐Péter R.‐Szabó P.‐Tolnai J.: Matematika az ált, gimn. III. o. számára, 12. kiadás, Tankönyvkiadó, Budapest, 1962) 194-200. o.