Feladat: 1300. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Berendi Emma ,  Bóta K. ,  Deák I. ,  Gyenes G. ,  Hegedűs Aletta ,  Hirka A. ,  Horányi S. ,  Huhn András ,  Kiss Györgyi ,  Lovász L. ,  Lux I. ,  Márki L. ,  Mátrai M. ,  Nagy Klára ,  Sófalvi M. ,  Szemkeő Judit ,  Szép A. ,  Varsányi Anikó ,  Vesztergombi Katalin 
Füzet: 1965/március, 111 - 113. oldal  PDF  |  MathML 
Témakör(ök): Pont körüli forgatás, Forgatva nyújtás, Kombinatorikai leszámolási problémák, Sakktáblával kapcsolatos feladatok, Négyzetrács geometriája, Feladat
Hivatkozás(ok):Feladatok: 1964/február: 1300. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Helyezzük el az egységnyi oldalú négyzetmezőkből álló ABCD=S sakktáblát a derékszögű koordináta-rendszerben úgy, hogy A, B, C csúcsa rendre az origóba, a (8;0), ill. a (8;8) pontba essék (1. ábra). Így hálózati pontok a sík egész x,y koordinátájú ún. rácspontjai közül azok, amelyekre

0≤x≤8,és0≤y≤8.(1)
A követelménynek megfelelő négyzeteket hálózati négyzeteknek nevezzük.
 
 
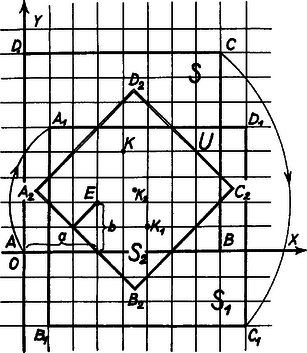2. ábra
 

Elég a kérdésre választ adnunk, ha a kiszemelt hálózati pont abban a T háromszögben vagy a kerületén van, amelynek csúcsai az origó, a (4;0) és a K(4;4) pont. Ugyanis T-t K körül egymás után háromszor 90∘-kal elforgatva, másrészt az így keletkezett 4 háromszöget az AC átlóra tükrözve a képek S-et hézagtalanul lefedik, minden hálózati pontra T egy hálózati pontja, vagy annak elforgatott képe, vagy elforgatott és tükrözött képe jut. A felsorolt szimmetriák minden hálózati négyzetet is hálózati négyzetbe visznek át, tehát minden hálózati pont ugyanannyi hálózati négyzetben lép fel csúcsként, mint a neki T-ben megfelelő hálózati pont.
Legyen T egy hálózati pontja E(a,b), vagyis
0≤b≤a≤4,(2)
és egy hálózati négyzet EFGH (betűzés az órajárással ellentétes irányban), legyenek F koordinátái (a+u,b+v), ahol egyidejűleg nem áll fenn u=0 és v=0.
H-t úgy kapjuk F-ből, hogy ezt E körül 90∘-kal balra elforgatjuk. A síknak azok a rácspontjai, amelyek a mondott módon S valamelyik hálózati pontjába vihetők át, abban az S1 négyzetben vagy a kerületén vannak, amely úgy keletkezik S-ből, hogy elforgatjuk E körül jobbra 90∘-kal. Eszerint F csak az S és S1 közös részében vagy annak kerületén lehet.
E az S egymás utáni oldalaitól rendre b, 8-a, 8-b, a távolságban van, ezért az S1 négyzet A1B1 oldalának egyenlete x=a-b (párhuzamos AD-vel), B1C1-é: y=b-(8-a), C1D1-é: x=a+8-b, D1A1-é: y=b+a. S és S1közös része az U téglalap. Alsó oldala AB-nek egy szakasza, mert S1-nek alsó B1C1 oldala mélyebben van vagy egybeesik AB-vel, hiszen (2) miatt b-8+a≤0. Hasonlóan jobbról BC (az x=8 egyenes) egy szakasza, felülről D1A1, balról A1B1 egy szakasza határolja U-t. Alapjának hossza 8-(a-b), ‐ ti. BC és A1B1 távolsága ‐, magasságáé b+a. Az oldalakon 1-gyel több hálózati pont van, mint ahány egység a hosszuk, ezért az U-hoz tartozó és az eddigiek szerint F számára szóba jövő hálózati pontok száma
(9-a+b)(a+b+1)-1=-a2+b2+8a+10b+8(3)
(a szorzatból 1-et levonunk, mert F≠E).
G-t úgy kapjuk F-ből, hogy az EF félegyenest E körül 45∘-kal balra forgatjuk és rámérjük az EG=2⋅EF szakaszt. Ezen a módon S hálózati pontjai csak olyan pontokból keletkezhetnek, amelyek az S-ből 1:2 arányú, E középpontú összehúzással és 45∘-os elforgatással keletkező S2 négyzetben vannak, azonban nem minden pont rácspont, ami hálózati pontba megy át. Ezek szerint EFGH akkor és csak akkor hálózati négyzet, ha F az U és S2 közös részében vagy annak határvonalán levő hálózati pont, és feladatunkat megoldottuk, ha (3)-ból levonjuk az S2-be nem tartozó hálózati pontok számát.
S2 az S1-ből is előállítható E körüli 1/2 arányú összehúzással és balra 45∘-os forgatással. Ebből könnyű belátni, hogy S2-nek K2 középpontja felezi a KK1 szakaszt, ahol K1 az S1 középpontja. A felezőpontba esik U középpontja is, így S2 átlói egybeesnek U szimmetriatengelyeivel, és S2 az U-ból négy egybevágó egyenlő szárú háromszöget zár ki. Eszerint elég meghatároznunk az U-ból az A2B2 egyenes által lemetszett háromszögben és a kerületének S2-höz nem tartozó részén levő hálózati pontok számát.
Az S2-t előállító forgatással az egységnyi négyzet oldalából e négyzet átlójának fele lesz. Így A2B2 az E-től b félátlónyi távolságban van, felezi az EL szakaszt, ahol L az U-nak az AB és A1B1 egyenesek metszéspontjában levő csúcsa. Eszerint a lemetszett háromszög befogóinak hossza b. Így AB-be eső oldalán b olyan hálózati pont van, amely nem tartozik S2-höz (a metszéspont már hozzátartozik), felfelé haladva az egymás utáni párhuzamos hálózati egyeneseken rendre 1-gyel kevesebb, így a 4 háromszög mondott hálózati pontjainak együttes száma
4[b+(b-1)+...+2+1]=2b(b+1).
Ezt (3)-ból kivonva az F-re szóba jövő hálózati pontok, és egyszersmind az E csúcsot tartalmazó hálózati négyzetek száma
-a2-b2+8a+8=8+a(8-a)+(8-b).
Ebből T összes hálózati pontjaira a 2. ábrán látható számokat kapjuk.
 
 
2. ábra
 

Huhn András (Szeged, Ságvári E. gyak. g. III.o. t.)
dolgozata alapján, egyszerűsítésekkel
 

Megjegyzés. A hálózati négyzetek számát a sakktábla összes hálózati pontjaira összegezve az összes hálózati négyzetek számának 4-szeresét kell kapnunk, amely szám a 846. gyakorlat*eredménye szerint 540. Könnyen ellenőrizhető, hogy ez teljesül is. ‐ A K-ban csúccsal bíró hálózati négyzetek 40-es létszámát már a 846. gyakorlatban is megkaptuk.
*K. M. L. 28 (1964) 74.