Kezdőlap


Feladat:	1295. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bak Zsuzsanna , Deák István , Huhn András , Kóbor György , Lux I. , Márki László , Mátrai Miklós , Nagy Klára , Pelikán József , Recski András , Sófalvi M. , Székely Gábor , Szép András
Füzet:	1964/november, 138 - 141. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletrendszerek, Csillagászati, földrajzi feladatok, Trigonometria, Gömbi geometria, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1964/január: 1295. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Két hely távolságának földrajzi koordinátáikból való számítására az 1214. feladatban a következő összefüggést használtuk:

\begin{matrix} cos ϑ = sin φ_{i} sin φ + cos φ_{i} cos φ cos (λ_{i} - λ), \end{matrix}

(1)

ahol

φ

λ

az egyik,

φ_{i}

λ_{i}

a másik hely földrajzi szélessége, ill. hosszúsága,

ϑ

pedig a szögtávolságuk, vagyis a (gömb alakúnak vett) Földnek a kérdéses helyekhez húzott sugarai által bezárt szög.
A kérdéses helyek koordinátái a térképről kb.

1 / 4

foknyi pontossággal leolvasva (ami esetünkben elegendő):

\begin{matrix} Kairó (K) : φ_{1} = 30^{\circ}, λ_{1} = 31^{\circ} 15'; Fokváros (F) : φ_{2} = - 34^{\circ}, λ_{2} = 18^{\circ} 30'; \\ Dakar (D) : φ_{3} = 14^{\circ} 45', λ_{3} = - 17^{\circ} 15' \end{matrix}

(a negatív előjel déli szélességet, ill. nyugati hosszúságot jelent).
Ha a továbbiakban

φ

λ

a kérdéses

P

hely koordinátáit jelöli,

ϑ

pedig az egymással egyenlő

P K

P F

P D

szögtávolságok közös értékét, akkor (1)-ben

i

helyére rendre az

1

2

3

indexet írva a

φ

λ

ϑ

ismeretlenekre

3

egyenletet kapunk.

ϑ

-t kiküszöbölhetjük két-két ilyen egyenlet kivonásával. Az

i = 1

és

i = 2

értékekkel adódó egyenletek kivonásával adódó egyenlet az alábbiak szerint alakul, ha benne a

cos (λ_{i} - λ)

tényezőt az addició-tétel alapján mindkétszer kifejtjük,

0

-ra redukálunk és rendezünk:

\begin{matrix} (sin φ_{1} - sin φ_{2}) sin φ + (cos φ_{1} cos λ_{1} - cos φ_{2} cos λ_{2}) cos φ cos λ + & (2) \\ + (cos φ_{1} sin λ_{1} - cos φ_{2} sin λ_{2}) cos φ sin λ = 0. \end{matrix}

i = 1

-gyel és

i = 3

-mal adódó egyenletek kivonásával ugyanilyen egyenletet kapunk, a

2

-es index helyén

3

-as indexszel. A zárójelbeli ‐ ismert ‐ együtthatók helyett vezessük be a következő jelöléseket:

\begin{matrix} sin φ_{1} - sin φ_{2} = A_{2}, sin φ_{1} - sin φ_{3} = A_{3}, \end{matrix}

\begin{matrix} cos φ_{1} cos λ_{1} - cos φ_{2} cos λ_{2} = B_{2}, & (3) \\ cos φ_{1} cos λ_{1} - cos φ_{3} cos λ_{3} = B_{3}, \\ cos φ_{1} sin λ_{1} - cos φ_{2} sin λ_{2} = C_{2}, \\ cos φ_{1} sin λ_{1} - cos φ_{3} sin λ_{3} = C_{3}, \end{matrix}

ezekkel a már csak

φ

-re és

λ

-ra vonatkozó egyenletrendszerünk:

\begin{matrix} A_{2} sin φ + B_{2} cos φ cos λ + C_{2} cos φ sin λ = 0, \\ A_{3} sin φ + B_{3} cos φ cos λ + C_{3} cos φ sin λ = 0, \end{matrix}

ahol a leolvasott adatok alapján:

\begin{matrix} A_{2} = 1, 0592, & B_{2} = - 0, 0458, & C_{2} = 0, 1862; \\ A_{3} = 0, 2454, & B_{3} = - 0, 1829, & C_{3} = 0, 7360. \end{matrix}

φ

kiküszöbölése végett osszuk az első egyenletet

A_{2} cos φ

-vel, a másodikat

A_{3} cos φ

-vel. Az utóbbit az előbbiből kivonva az egyenlet minden tagja vagy csak a

cos λ

, vagy csak a

sin λ

tényezőt tartalmazza ismeretlen gyanánt, így ezek hányadosa kiszámítható:

\begin{matrix} tg φ + \frac{B_{i}}{A_{i}} cos λ + \frac{C_{i}}{A_{i}} cos λ = 0, (i = 2, 3) & (4) \\ (\frac{B_{2}}{A_{2}} - \frac{B_{3}}{A_{3}}) cos λ + (\frac{C_{2}}{A_{2}} - \frac{C_{3}}{A_{3}}) sin λ = 0, \\ tg λ = \frac{A_{2} B_{3} - A_{3} B_{2}}{C_{2} A_{3} - C_{3} A_{2}} . & (5) \end{matrix}

(A végzett osztások megengedettek voltak, mert ‐ esetünkben ‐ sem

A_{2}

, sem

A_{3}

, sem (5) nevezője nem

0

, továbbá az ismeretlen

φ

-ről is tudjuk, hogy koszinusza különböző

0

-tól, ugyanis a

cos φ = 0

egyenlőségből

φ = \pm 90^{\circ}

következnék, vagyis hogy

P

gyanánt az Északi-sark és a Déli-sark jönne szóba, ez viszont nyilván csak akkor megoldás, ha mind a három adott hely földrajzi szélessége egyenlő. (Ez esetben

A_{2} = A_{3} = 0

is beállna.)

λ

ismeretében

φ

értéke (4) bármelyik egyenletéből kiszámítható. Számadatainkkal

λ = 13^{\circ} 58'

, és

φ = - 0^{\circ} 1'

, illetőleg a kiindulási adatokhoz hasonlóan, a kapott koordinátákat is

1 / 4

fokra kerekítve, a keresett pont

P (0^{\circ}

14^{\circ})

. A

180^{\circ}

-kal nagyobb

λ

értéket mindjárt mellőzhettük, mert a

194^{\circ}

-os hosszúsági kör ‐ más néven a

166^{\circ}

nyugati hosszúságú délkör ‐ nem megy át Afrikán. (A ,,kör'' szót itt a földrajzban szokásos értelemben vettük, geometriai szempontból a délkörök félkörök.) A

P

pont Afrikában van, Gabon és a Kongói Köztársaság (volt Francia Kongó) határvidékén, ennélfogva a feladat első kérdésére a válasz igenlő,

P

távolsága (1) szerint mindhárom várostól

34, 2^{\circ}

, kb.

3800

km.

II. Az eredmény szerint egy csapásra a feladat második kérdésére is megkaptuk a választ, hiszen

P

az Egyenlítőn adódott, és

P

mind a három kérdéses főkörön rajta van. E főkörök az Egyenlítőt a fent említett

166^{\circ}

nyugati hosszúságú pontjában is metszik, a Főnix szigetektől ÉK felé, kb.

600

km-ny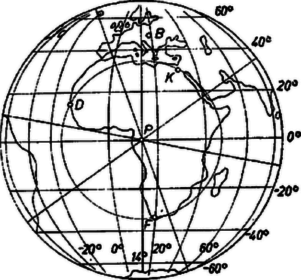ire.

Ha ez a véletlen nem adódott volna, akkor a kérdéses pontokat pl. a

K

-tól és

F

-től egyenlő távolságra haladó főkörre nézve (2)-ből számítottuk volna. Ezt az egyenletet ugyanis abból a követelményből kaptuk, hogy a

φ

λ

koordinátájú pontnak egyenlő szögtávolságra kell lennie

K

-től és

F

-től, ez tehát az előírt tulajdonságú pontok mértani helyének egyenlete (a Föld felületének pontjaira vonatkoztatva). Ez a mértani hely a Földnek valóban főköre. Ugyanis a térnek

K

-tól és

F

-től egyenlő távolságra levő pontjai az

F K

szakasz felező merőleges síkján vannak, és ez a sík átmegy a gömb

O

középpontján, mert

O K = O F

, tehát főkört metsz ki. Így (2) a főkör egyenlete.
Az Egyenlítő pontjaira

φ = 0^{\circ}

(ez az Egyenlítő egyenlete, írható

sin φ = 0

, vagy

cos φ = 1

alakban is), tehát a keresett pontok

λ_{0}

hosszúságaira (2)-ből a (3) jelölésekkel

\begin{matrix} B_{2} cos λ_{0} & + C_{2} sin λ_{0} = 0, \\ tg λ_{0} & = - B_{2} / C_{2}, \end{matrix}

(feltéve, hogy

C_{2} \neq 0

, a kizárt esetben pedig

λ_{0} = \pm 90^{\circ}

). Adatainkkal az Afrikába eső metszéspont a

K F

körre

13^{\circ} 49'

K D

-re

13^{\circ} 57'

F D

-re

14^{\circ} 0'

, a leolvasási kerekítésekre tekintettel egybeesőknek vehetők.
Huhn András (Szeged, Ságvári E. g. III. o. t.)
Kóbor György (Budapest, Rákóczi F. g. III. o. t.)

Megjegyzések. 1. Az általános megoldás bővebb elemzésébe nem bocsátkoztunk bele, tekintettel a feladat konkrét jellegére.
2. Több dolgozat síkgeometriai úton próbálta megoldani a feladatot, vagyis a sík térképen látható helyzetet véve valóságnak. Ez a szereplő városok közti nagy távolságok mellett nem elfogadható. A megoldás kulcsát a feladathoz fűzött jegyzet az olvasók kezébe is adta. Így a feladat lényegében leszűkült egy egyszerű goniometrikus egyenletrendszer megoldására.
3. Vázlatunk a Földet a

P

pontbeli érintősíkra vetítve mutatja, merőleges vetítéssel. Így a felező merőleges főkörök vetülete a Föld képének egy-egy átmérője, és a

D

F

K

pontokon átmenő gömbi kis-kör vetülete kör. ‐ Ez a vázlat természetesen nem használható a feladat ,,síkbeli'' megoldásához, hiszen csak a

P

pont ismeretében, utólag készülhetett.