Kezdőlap


Feladat:	1294. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bóta Károly , Csörnyei Zoltán , Deák István , Fekete E. , Huhn A. , Lovász László , Nagy Klára , Pelikán József , Siket Aranka , Szemkeő Judit
Füzet:	1964/november, 136 - 138. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Szögfüggvények, síkgeometriai számítások, Szabályos sokszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1964/január: 1294. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A szabályos ötszög bármelyik két csúcsát vagy egy oldal, vagy egy átló köti össze, és mind az öt átló egyenlő; így a $P R$ szakasz vagy oldala, vagy átlója az ötszögnek. Az első esetben $P$ és $R$ szomszédos csúcsok, a $P$ -vel szomszédos másik csúcs $k_{1}$ -en lesz, ebből kell kimetszenünk alkalmas körrel ‐ mert csak körzőt használhatunk ‐, az $R$ -rel szomszédos másik csúcs pedig $k_{2}$ -n lesz. A második esetben $P$ , $R$ szemben fekvő csúcsok, így a $P$ -vel szemben levő másik csúcs lesz $k_{1}$ -en, az $R$ -rel szemben levő másik csúcs pedig $k_{2}$ -n. Az első esetnél maradva kézenfekvő arra gondolni, hogy a $P$ -vel szomszédos $A$ csúcsnak $k_{1}$ -ből való kimetszését egy az $R$ körül írt további körrel végezte az eljárás elveszett befejezése. Ekkor $k_{7}$ sugara a $P R$ oldalú szabályos ötszög átlója. Ugyanekkora sugarú, a $P$ körül írt kör kimetszhetné $k_{2}$ -ből az $R$ melletti $C$ csúcsot, és e két kör metszéspontja megadhatná az ötszögnek a $P R$ oldallal szemben levő $B$ csúcsát, vagyis az átlót ismerve a hátra levő két lépésben befejezhetnénk a szerkesztést. Így ‐ ha feltevésünk találó ‐ az átlónak már csak a felhasználására futja a további két lépésből, tehát az átló hosszának már meg kell lennie az ábrán, annak a $k_{6}$ megrajzolása utáni fázisában ‐ éspedig a megnevezett pontok valamelyik párjának távolsága gyanánt, ‐ hiszen az első hat kör számos további metszéspontot ad, és a könyv bizonyára csak a tovább felhasználandó pontokra vezetett be betű-jelölést. Továbbmenve az átló hosszát megadó pontpár egyik tagja a $k_{6}$ révén kapott, $U$ vagy $T$ , különben ezek megszerkesztése és megjelölése felesleges volna, a szerkesztés kevesebb kör rajzolásával lenne befejezhető.

1. ábra

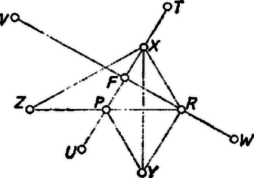
A szabályos ötszög átlójának és oldalának aránya az egy átló által lemetszett egyenlő szárú háromszögből^{$^{*}$}

2 cos 36^{\circ} = (\sqrt[]{5} + 1) / 2

. Megmutatjuk, hogy egységnek véve

P

és

R

távolságát,

P

és

T

távolságának mértékszáma éppen egyenlő ezzel az arányszámmal.

P R X

és

P R Y

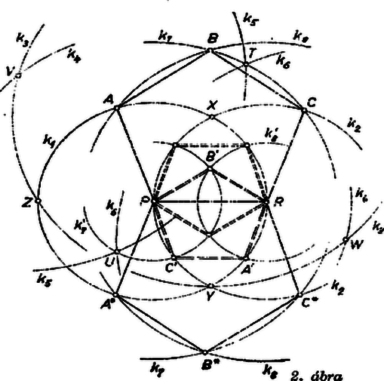
egyenlő oldalú háromszögek (1. ábra, ezen a jobb áttekintés érdekében a köröket mellőztük, és a szóba jövő távolságokat egyenesszakasszal meg is rajzoltuk), ezért

X Y = \sqrt[]{3}

, továbbá

X P Y ∢ = 120^{\circ}

. Az

X V P W

négyszög rombusz, így

V W

merőlegesen felezi

P X

-et, továbbá

V W^{2} = 4 X Y^{2} - P X^{2} = 11

, mivel minden paralelogrammában az átlók négyzetösszege egyenlő az oldalak négyzetösszegével.

X P Y

és

X P Z

egybevágó háromszögek, mert oldalaik páronként egyenlők, így

X P Z ∢ = 120^{\circ}

, ezért

Z

rajta van a

P

R

pontokkal meghatározott egyenesen, tehát

R Z = 2

. A fentiekhez hasonlóan az

U V T W

idom rombusz, és

U T

merőlegesen felezi

V W

-t, tehát

U

és

T

rajta vannak a

P

-vel és

X

-szel meghatározott egyenesen, és

U T^{2} = 4 R Z^{2} - V W^{2} = 5

. Mostmár

P X

V W

és

U T

közös felezőpontját

F

-fel jelölve

\begin{matrix} P T = P F + F T = \frac{P X + U T}{2} = \frac{1 + \sqrt[]{5}}{2}, \end{matrix}

ezt akartuk bizonyítani, és ennek alapján ‐ mint láttuk ‐ a

k_{7} = P (P T)

és

k_{8} = R (P T)

köröket megrajzolva a hiányzó

A

B

C

csúcsok kiadódnak,

A

B

C

R

P

egy szabályos ötszög csúcsai.
Hasonlóan jutunk célhoz, ha az adott

P

-t és

R

-et a keresett szabályos ötszög két nem szomszédos csúcsának tekintjük, és keressük az ábra

k_{6}

berajzolása utáni fázisában az ötszög oldalának hosszát. Az oldal az átlónak

1 / (2 cos 36^{\circ}) = 2 / (\sqrt[]{5} + 1) = (\sqrt[]{5} - 1) / 2

része, ezt a fentiek szerint megadja

P

és

U

távolsága, tehát a

k'_{7} = P (P U)

k'_{8} = R (P U)

körök metszik ki

k_{2}

-ből, ill.

k_{1}

-ből, ill. egymásból az ötszög hiányzó csúcsait.
Mindkét esetben két ötszöget kapunk, ezek egymás tükrös párjai a

P

-n és

R

-en átmenő egyenesre.

Nagy Klára (Makó, József A. g. III. o. t.)

3. ábra

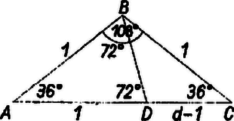
Megjegyzés. A szabályos ötszög átlójának és oldalának arányát szögfüggvény felhasználása nélkül is meghatározhatjuk. Legyen az

A B C

háromszögben

A B = B C = 1

A C = d

és

A B C ∢ = 108^{\circ}

. Mérjük rá

A B

-t az

A C

oldalra

A

-tól, legyen a végpont

D

. Ekkor

C A B ∢ = 36^{\circ}

;

A B D ∢ = A D B ∢ = 72^{\circ}

;

D B C ∢ = 36^{\circ} = D C B ∢

; tehát

C D B △ \sim A B C △

;

C D : C B = A B : A C

, azaz

(d - 1) :

: 1 = 1 : d

;

d^{2} - d - 1 = 0

, és ennek pozitív gyöke

d = (\sqrt[]{5} + 1) / 2

^{$^{*}$}Felhasználjuk

cos 36^{\circ}

-nak az 1213. feladatban idézett értékét, lásd K. M. L. 27 (1963/9. 19. o.)