Kezdőlap


Feladat:	1293. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bódi Zoltán , Bóta Károly , Bulkai L. , Bummer Gertrúd , Deák István , Halász Szilvia , Horányi Sándor , Huhn A. , Jahn László , Kalmár T. , Kiss Katalin , Laczkovich Miklós , Lux I. , Mátrai Miklós , Nagy Klára , Nagy László , Palócz A. , Pelikán József , Radó A. , Siket Aranka , Sükösd Csaba , Szabó Mihály , Szemkeő Judit , Szép András
Füzet:	1964/november, 134 - 136. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyéb sokszögek hasonlósága, Tengelyes tükrözés, Trapézok, Pitagoraszi számhármasok, Héroni számhármasok, Feladat
Hivatkozás(ok):	Feladatok: 1964/január: 1293. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha egy trapéz megfelel a feladat követelményeinek, akkor egyik alapja egy-egy szárral és átlóval két olyan háromszöget alkot, amelyek oldalainak mértékszáma egész, egy oldaluk egyenlő, magasságuk $24$ , és az egyenlő oldalak mentén egymásra téve őket a közös oldallal szemben levő csúcsok távolsága is egész. Ilyen háromszögek keresése eredményes lesz összetolással, illetve részbeni fedéssel azokból a pythagorászi háromszögekből (1. ábra), amelyek egyik befogószáma $m = 24$ . Így a magasságok talppontjainak az alap végpontjaitól mért távolságai egész számok, ezért a trapéz másik alapja is egész lesz.

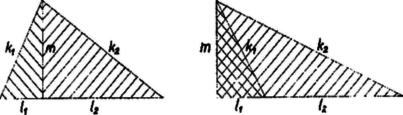1. ábra

A mondott számhármasok átfogószámát

k

-val, másik befogószámát

l

-lel jelölve

m^{2} = 576 = k^{2} - l^{2} = (k - l) (k + l)

. Itt a jobb oldal tényezői egész számok, továbbá párosak. Ugyanis szorzatuk páros, ezért az egyik tényező páros, így viszont összegük,

2 k

, és különbségük,

2 l

, csak akkor páros, ha a másik tényező is páros. Eszerint a

k

l

24

pythagorászi számhármasokat

576

-nak két különböző páros szám szorzata gyanánt való előállításából kapjuk (ugyanis

k - l < k + l

). Hét ilyen van, lásd az I. táblázat egy-egy oszlopát.

\begin{matrix} I. & k - l = 2, & 4, & 6, & 8, & 12, & 16, & 18; \\ k + l = 288, & 144, & 96, & 72, & 48, & 36, & 32; \\ k = 145, & 74, & 51, & 40, & 30, & 26, & 25; \\ m = 24, & l = 143, & 70, & 45, & 32, & 18, & 10, & 7. \end{matrix}

Két-két (különböző, ill. egyenlő)

l

-befogó összegét és különbségét a II. táblázaton állítottuk össze, amelyen minden egyes

l

-értékhez egy sor és egy oszlop tartozik, az

i

-edik sor és a

j

-edik oszlop közös mezején

i \leq j

esetén (a jobbra lejtő átlón és tőle jobbra fölfelé) az

l_{j} + l_{i}

összeg áll,

i > j

esetén pedig (balra lefelé) az

l_{j} - l_{i}

különbség.
A táblázat

49

racionális háromszöget ad az

m = 24

magasság-számhoz. Szóba jönnek továbbá maguk a felhasznált pythagorászi háromszögek is, hiszen amennyiben létezik derékszögű a trapézek között, annak származtató háromszögei közül az egyikben az alapon derékszög van.

\begin{matrix} II. & l_{1} = 7, & l_{2} = 10, & l_{3} = 18, & l_{4} = 32, & l_{5} = 45, & l_{6} = 70, & l_{7} = 143 \\ l_{1} = 7 & 14 & 17 & 25 & 39 & 52 & 77 & 150 \\ l_{2} = 10 & 3 & 20 & 28 & 42 & 55 & 80 & 153 \\ l_{3} = 18 & 11 & 8 & 36 & 50 & 63 & 88 & 161 \\ l_{4} = 32 & 25 & 22 & 14 & 64 & 77 & 102 & 175 \\ l_{5} = 45 & 38 & 35 & 27 & 13 & 90 & 115 & 188 \\ l_{6} = 70 & 63 & 60 & 52 & 38 & 25 & 140 & 213 \\ l_{7} = 143 & 136 & 133 & 125 & 111 & 98 & 73 & 286 \end{matrix}

Nyilvánvaló, hogy minden

l_{j} + l_{i} (i \neq j)

alapú háromszögből az alap felező merőlegesén való tükrözéssel egy racionális szimmetrikus trapézt kapunk, ennek rövidebb alapja

l_{j} - l_{i}

, az ilyenek száma tehát

21

. Ha ugyanígy egy derékszögű háromszöget tükrözünk

l_{i}

felező merőlegesére,

7

racionális téglalap keletkezik. Tulajdonképpeni feladatunknak azonban a nem szimmetrikus racionális trapézok előállítását tartjuk, ezek érdekesebbek, mert száraik és átlóik különböző egész számok. Ilyen trapéz alapjai gyanánt a táblázatnak csak az ismétlődő számai szerepelhetnek, ezeket kiemeltük kövér nyomtatással.

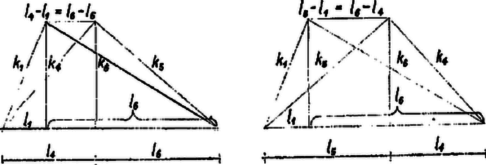2. ábra

Két egyező alaphosszra a két Heron-háromszöget kétféleképpen helyezhetjük rá, ha egyikük sem egyenlő szárú. Pl. a

\begin{matrix} 77 = l_{1} + l_{6} = l_{4} + l_{5} \end{matrix}

(1)

egyenlőség alapján a

77

egységnyi alap

l_{1}

részének végpontjára vagy az

l_{4}

, vagy az

l_{5}

rész végpontját illeszthetjük rá, és így a másik alap mértékszámán az első esetben

l_{4} - l_{1} = l_{6} - l_{5} = 25

, a másodikban

l_{5} - l_{1} = l_{6} - l_{4} = 38

adódik (ezek természetesen ugyancsak ismétlődő alaphosszai a táblázatnak; 2. ábra), az egyenlőségek (1)-ből adódnak átrendezéssel. A trapéz átlóit és szárait a megfelelő számhármasok

k_{1}

k_{4}

k_{5}

k_{6}

átfogószámai adják.

\begin{matrix} Alapok & Szárak & Átlók & Magasság \\ III. & 14 & 25 & 25 & 30 & 25 & 40 & 24 \\ 25 & 25 & 25 & 25 & 30 & 40 & 24 \\ 25 & 38 & 40 & 51 & 25 & 74 & 24 \\ 25 & 52 & 30 & 51 & 25 & 74 & 24 \\ 25 & 63 & 25 & 51 & 30 & 74 & 24 \\ 25 & 77 & 25 & 51 & 40 & 74 & 24 \\ 38 & 77 & 25 & 40 & 51 & 74 & 24 \\ 52 & 63 & 25 & 30 & 51 & 74 & 24 \end{matrix}

Hasonlóan végigmenve a táblázat összes egyező számpárjain, a III. táblázaton felsorolt

8

racionális trapézhez jutunk. A

63

52

38

alapszám két-két előfordulásából is 2‐2 trapéz adódik, viszont a

25

-ös három előfordulása háromféleképpen állítható párba, ezekből

3 \cdot 2 = 6

trapéz, a

14

alapszám előfordulásaiból pedig

1

, mert a

14

25

25

háromszög szimmetrikus

m

-re. Így a fenti trapézeket mindkét alapjuk révén megkapjuk, kivéve a 2. sorbelit, amely racionális paralelogramma (rombusz).

Nagy László (Győr, Benedek-rendi Czuczor G. g. III. o. t.)
Laczkovich Miklós (Budapest, Fazekas g. II. o. t.)

Megjegyzések. 1. A feladat nem kívánta az

m = 24

magasságszámhoz tartozó összes racionális trapézek előállítását; a fentieket azért közöltük, mert különböző versenyzők más-más megoldást találtak.
2. A fentieken kívül további megoldás nincs, megmutatjuk ugyanis, hogy ha egy háromszög

a

b

c

oldalainak és az

a

oldalhoz tartozó

m

magasságának hossza egész szám, akkor

m

talppontjának az

a

végpontjaitól mért

\begin{matrix} a_{b} = \sqrt[]{b^{2} - m^{2}} = \sqrt[]{p} és a_{c} = \sqrt[]{c^{2} - m^{2}} = \sqrt[]{q} \end{matrix}

távolságai is egész számok. Ugyanis ezeknek vagy az összege egyenlő

a

-val, vagy (ha az

a

oldal egyik végpontjában tompaszög van) a pozitív különbsége:

\begin{matrix} \sqrt[]{p} \pm \sqrt[]{q} = a . \end{matrix}

(2)

Ebből négyzetreemeléssel és rendezéssel

\begin{matrix} \pm 2 \sqrt[]{p q} = a^{2} - p - q = r, \end{matrix}

egész szám, mert

p

q

egészek. Így

\pm \sqrt[]{q} = r / 2 \sqrt[]{p}

és (2) alapján mindkét négyzetgyök racionális szám, ugyanis

\begin{matrix} \sqrt[]{p} + \frac{r}{2 \sqrt[]{p}} = \frac{2 p + r}{2 \sqrt[]{p}} = a, \sqrt[]{p} = \frac{2 p + r}{2 a}, \sqrt[]{q} = a - \sqrt[]{p} = \frac{r + 2 q}{2 a} . \end{matrix}

Így egészek is, mert ha egy racionális szám nem egész, akkor négyzete sem az.
Eszerint feltételeink mellett

b

m

a_{b}

és

c

m

a_{c}

pythagorászi számhármasok, a fentiekben az adott magassághoz megkaptuk az összes racionális trapézokat.

Pelikán József (Budapest, Fazekas M. g. II. o. t.)