Feladat: 1292. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Babai László ,  Bóta Károly ,  Csörnyei Z. ,  Deák István ,  Erdélyi Katalin ,  Huhn A. ,  Kelemen G. ,  Kiss Katalin ,  Kövér Ákos ,  Laczkovich M. ,  Lux I. ,  Máté Mária ,  Mátrai Miklós ,  Nagy Klára ,  Pelikán József ,  Siket Aranka ,  Szemkeő Judit ,  Sövényházy Mária ,  Vesztergombi Katalin 
Füzet: 1964/november, 131 - 133. oldal  PDF  |  MathML 
Témakör(ök): Analógia, mint megoldási módszer, Kombinatorikus geometria síkban, Feladat
Hivatkozás(ok):Feladatok: 1964/január: 1292. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha van minden páratlan n(≥3) esetén érvényes elv a kívánt elrendezéshez, akkor azt n=3-ra alkalmazva az adódó elrendezésnek elő kell fordulnia az n=3 eset összes megoldásai között. Ezért előállítjuk az n=3 eset összes megoldásait, majd megkísérlünk belőlük olyan általános elveket kiolvasni, amelyek bármely n páratlan szám esetében megfelelnek.
Legyen az oldalak összege S. A 3 oldal együttes összegében minden előírt szám előfordul egyszer, a csúcsokon álló három szám pedig mégegyszer. Így a csúcsokra előbb a legkisebb három, majd a legnagyobb három számot választva alsó, ill. felső korlátot kapunk S-re:

3S≥(1+2+3+4+5+6)+(1+2+3)=21+6,S≥9,(1)3S≤21+(6+5+4),S≤12.



Tekintsük először az S=9 és S=12 értékeket. S és a csúcsokon álló számok meghatározzák az oldalfelező pontokhoz rendelendő számokat. A kiválasztott három számot szimmetriáktól eltekintve csak egyféleképpen lehet elrendezni a csúcsokon. Mindkét próbálkozásból egy-egy megoldást kapunk (1. ábra I‐II.).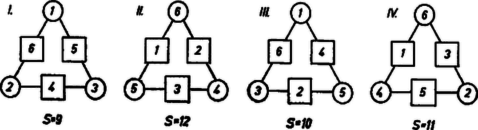
 
 
1. ábra
 

Vegyük észre, hogy a két megoldásban a megfelelő helyeken álló számpárok összege minden esetben 7. Ez azt jelenti, hogy bármelyik megoldás bármelyik száma helyére a másik megoldásban az a szám lép, amely neki az előírt számok növekvő felsorolásában a középpontra (a 3 és 4 közti hézagra) nézve tükrös helyzetű párja. Ezzel a helyettesítéssel bármely más megoldásból is, továbbá bármely páratlan n esetén is kapunk egy új megoldást, mert a páros cserékből álló helyettesítés után is minden előírt szám fellép, és az összegek is egyenlők, az
a1+a2+a3=S= állandó összeg helyén (7-a1)+(7-a2)+(7-a3)=21-S= állandó összeg adódik, általában pedig az
1,2,3,...,n,n+1,...,2n-2,2n-1,2n(2)
számok elrendezése esetén
(2n+1-a1)+(2n+1-a2)+(2n+1-a3)=3(2n+1)-S.
Így a hátralevő S=10 és S=11 lehetőségek közül elég pl. az elsővel próbálkoznunk.
(1) szerint akkor adódik S=9 helyén 1-gyel nagyobb érték, ha a csúcsokon álló számok 1+2+3 összegét 3-mal növeljük. Nem vehető azonban 1+2+6, mert így 1 és 2 közé 7-et kellene írnunk, ami nem megengedett. Így csak 1+3+5 állhat a csúcsokon, ebből adódik ‐ mindjárt a fenti tükrözés alkalmazásával ‐ az 1. ábra III. és IV. megoldása. (Nincs ugyanis több megoldás, mert a csúcsokra a 2, 3, 4 számokat véve a 6-os szám egyik oldal közepére sem írható, mindenképpen túllépnők S=10-et.) ‐ Ebben a két megoldásban az összes páratlan (ill. páros) számaink kerültek a csúcsokra.
Ha n-szöget véve az S=9 esetén talált megoldás mintájára, a (2) sorozat első felének egymás utáni tagjait pl. az óramutató járásáéval ellentétes irányban haladva rendeljük hozzá a csúcsokhoz: nem kapunk megoldást. Így ugyanis az egymás utáni oldalak végpontjain álló számpárok összegének 1+2=3, 2+3=5, 3+4=7,..., (n-1)+n=2n-1, n+1 sorozata 2-esével növekvő sorozat (eltekintve az utolsó tagtól), ezért az oldalfelező pontokhoz az összeg-követelmény alapján hozzáírandó S-3, S-5, S-7,... számok sorozata 2-esével csökkenő sorozat, tehát ezek a számok nem alkothatják (2) második felét.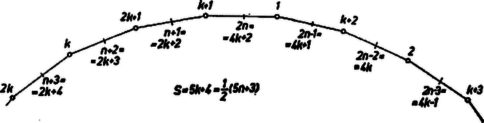
 
 
2. ábra
 

Az n=3 eset S=9-es megoldásáról azonban leolvasható egy más, bár kevésbé kézenfekvő rendszeresség is: az óramutató járásának irányában haladva mondhatjuk, hogy az 1, 2, 3 számokat minden második csúcshoz rendeltük hozzá. Írjuk tehát a (2) sorozat első felének egymás utáni számait is rendre az n-szög minden második csúcsához. Ennek során az n-szög első körüljárásában csak a páratlan sorszámú csúcsokat töltjük be (az 1-essel betöltött csúcsot véve elsőnek). Ha n=2k+1, akkor a 2k+1-edik, vagyis az 1-es előtti csúcshoz a k+1-et írjuk, mert 2k+1=2(k+1)-1 a páratlan számok sorozatában a k+1-edik tag. A második körüljárásban az előbb átlépett csúcsokhoz az 1 és 2 közé k+2 kerül, 2 és 3 közé k+3,..., végül az utolsó üres csúcsra, k+1 elé az utolsó tervbe vett szám, a 2k+1.
Ekkor az 1-es csúcs előtti oldal két végpontján (k+1)+1=k+2 az összeg, majd az 1-es csúcs utáni oldalak végpontjain egymás után 1+(k+2)=k+3, (k+2)+2=k+4, 2+(k+3)=k+5, (k+3)+3=k+6,..., rendre 1-gyel nagyobb összeg adódik, mert két egymás utáni oldal egyik száma közös, a nem közös szám pedig a későbbi oldalon 1-gyel nagyobb, mint a megelőző oldalon. Az utolsó ‐ az 1-es előtti második ‐ oldal végpontjain (2k+1)+(k+1)=3k+2 az összeg, és ez valóban n=2k+1-edik tagja a természetes számok felsorolásának, k+2-től kezdve: (k+2)+(n-1)=(k+2)+2k=3k+2.
Ha már most az oldalak felezőpontjaihoz a legutóbbi felsorolás rendjében a 2n,2n-1,2n-2,...,n+2,n+1 számok 1-esével csökkenő sorozatának tagjait rendeljük hozzá, akkor az n-szög minden oldalán nyilvánvalóan ugyanannyi az összeg, másrészt az előírt számok mindegyikét egyszer felhasználtuk, tehát megoldást kaptunk. Ezzel az állítást bebizonyítottuk.
Hasonlóan látható be, hogy megfelelő hozzárendelést kapunk az n=3, S=10 eset következő általánosításával is: először az 1,3,5,...,2n-1 páratlan számokat rendeljük hozzá egymás után az n-szög minden második csúcsához, majd pedig a 2n,2n-2,2n-4,...,4,2 páros számokat az egymás utáni oldalak felezőpontjaihoz, (n+1)/2 és 1 közé 2n-et írva, a következőket pedig az előbbivel megegyező irányú körüljárás mentén haladva. ‐ Önállóan megfogalmazható az n=3, S=12, ill. S=11 esetben talált megoldás általánosítása is (minden második csúcsra a ,,nagy'' számokat: 2n,2n-1,2n-2,...,n+1-et, ill. a páros számokat: 2n,2n-2,2n-4,...,4,2-t). A négy hozzárendelési elvet n=7 esetére bemutatjuk (3. ábra).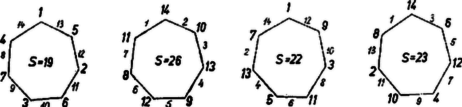
 
 
3. ábra
 

 
Szemkeő Judit (Budapest, Ságvári E. gyak. lg. III. o. t.)