| Feladat: | 1291. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Bóta K. , Bulkai L. , Czina Ferenc , Deák I. , Hortobágyi József , Lovász L. , Mátrai M. , Nagy Márta , Pelikán J. , Siket Aranka , Sófalvi M. , Szabó M. , Szalay M. , Szemkeő Judit , Szép András , Vesztergombi Katalin | ||
| Füzet: | 1965/január, 11 - 14. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Másodfokú (és arra visszavezethető) egyenletek, Egyenlő szárú háromszögek geometriája, Körülírt kör, Beírt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek szerkesztése, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1964/január: 1291. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Legyen a keresett háromszög (). Jelöljük a körülírt kör, ill. a beírt kör sugarát -rel, ill. -val, felezőpontját -vel, a körülírt kör -vel átellenes pontját -vel, a beírt kör érintési pontját az száron -vel (1. ábra). 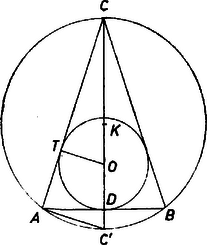 Kifejezhetjük az
Az háromszög -nál derékszögű, így a befogó, továbbá a magasság mértani közép tulajdonsága szerint végül a beírt kör érintője és szelője közt a következő összefüggés áll fenn, mivel (az egyenlő szárú háromszög szimmetriatengelye) átmegy a kör középpontján:
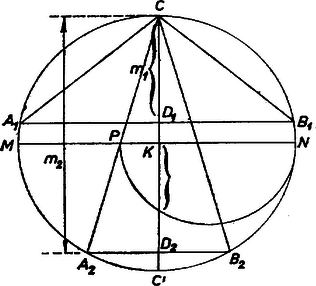 Ha , akkor mindig létezik a feltételeket kielégítő háromszög. Megszerkeszthető pl. a következő módon. Egy sugarú, középpontú körben megszerkesztünk két egymásra merőleges és átmérőt, utóbbira rámérjük az távolságot (2. ábra). A átmérőjű félkör -vel való metszéspontjának -tól mért távolsága . Ezzel megszerkesztjük az , ill. távolságot és rámérjük -ből a átmérőre; a , ill. végpontban az átmérőre emelt merőleges metszi ki a körből a keresett háromszög , , ill. , csúcsait. Ha , akkor , és egy háromszöget kapunk, különben kettőt. Be kell látnunk, hogy az és háromszögek megfelelnek a követelményeknek. Mindkettő egyenlő szárú, körülírt körének sugara . Beírt körük , ill. sugarát a háromszög területére vonatkozó ( ) képletből határozhatjuk meg, ahol -sel a kerület felét jelöltük. Mivel az háromszögek derékszögűek, fennállnak rájuk a (2), (3) összefüggések. Így ahol az 1 indexnek mindkét alternatív előjelből a fölső, a 2 indexnek mindkettőből az alsó felel meg. Az első tag így alakítható tovább: Így végül azt kaptuk, hogy Szép András (Budapest, Rákóczi F. G. IV. o. t.) Megjegyzések: 1. Aszerint lesz nagyobb vagy kisebb -nál, vagy egyenlő vele, amint , és a beírt kör középpontja ebben a sorrendben sorakozik a szakaszon, vagy , , sorrendben, vagy és egybeesik. Az egyes esetekben , ill. , ill. . Összehasonlítva ezt az -re kapott formulákkal és megfigyelve, hogy a harmadik eset csak esetben következhet be, a összefüggést nyerjük. Ezt az összefüggést bizonyítottuk a 788. gyakorlatban is. Mint ott is említettük, az összefüggés minden háromszögre fennáll, nemcsak az egyenlő szárúakra. 2. Kifejezhetjük az (1)-ben fellépő távolságokat a háromszögnek pl. az oldalával is: (2)-ből ; ezt (3)-ba és (4)-be, és az és -re így adódó kifejezéseket (1)-be beírva -re kapunk egyenletet, amit 3. Igen egyszerű egyenlet adódik -re is: az és háromszögek hasonlóságából , innen és (2)-ből 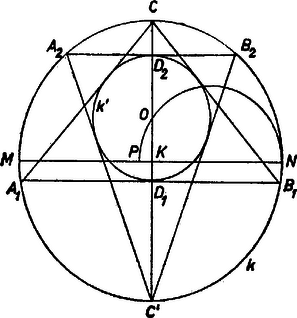 II. megoldás. Megoldható a feladat az 1. megjegyzésben talált és már a 788. gyakorlatból is ismert összefüggés alapján. Továbbra is a fenti jelöléseket használjuk. A beírt és körülírt kör középpontjának távolsága a mondott összefüggés szerint A szerkesztést számítással követve egyszerűen kapjuk a távolságból a háromszög magasságát ‐ ill. -ből -t ‐, ezek ismeretében pedig az alap felét (, 2) és az (ill. ) szárat a derékszögű háromszögből számíthatjuk ki. Legyen a átmérőnek -hoz közelebbi végpontja . Ekkor , , ezekből és így ‐ (1)-et is figyelembe véve ‐ esetén a külső négyzetgyökök alatt is pozitív szám áll, mert nyilvánvalóan belsejében van, és ugyanez áll -re is, különben -ből következnék, ami lehetetlen. Czina Ferenc (Makó, József A. G. III. o. t.) Hortobágyi József (Budapest, Bláthy O. Erősár. Ip. T. IV. o. t.) |