| Feladat: | 1288. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Csontos gy. , Csörnyei Zoltán , Deák István , Ferenczy M. , Gyenes A. , Horányi Sándor , Hortobágyi József , Huhn András , Kalmár T. , Kóbor Gy. , Kóbor György , Kövér Ákos , Láng A. , Laufer Judit , Lehel Csaba , Lovász László , Lukács Lídia , Lux I. , Márki László , Mátrai Miklós , Nagy László , Nagy Péter Tibor , Palócz A. , Patkós A. , Pelikán József , Siket Aranka , Sófalvi M. , Sükösd Csaba , Szalkai István , Székely Gábor , Szemere J. , Szemkeő Judit , Szendrői Annamária , Szép András , Veres Ferenc , Vertse M. , Vesztergombi Katalin , Volkay J. | ||
| Füzet: | 1964/október, 73 - 75. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Térelemek és részeik, Kocka, Kombinatorikai leszámolási problémák, Feladat, Térgeometria | ||
| Hivatkozás(ok): | Feladatok: 1963/december: 1288. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Legyen a kocka két párhuzamos lapja és úgy, hogy és párhuzamos élek. Vizsgáljuk először pl. az testátló felező és harmadoló pontjaiban az átlóra merőlegesen állított síkokat. Azt állítjuk, hogy az utóbbi két sík a , , és a , , csúcsokon átmenő és sík, más szóval az -ból, ill. -ből induló élek végpontjain átmenő sík. 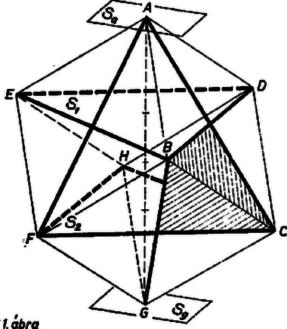 Ez következik abból, hogy egyrészt az , , egybevágó háromszögek , , ill. csúcsából húzott magasság ugyanabban a pontban metszi -t, tehát az ebben a pontban -re állított merőleges sík, és hasonlóan is merőleges -re. Másrészt -ban és -ben is , ill. merőleges síkot állítva -re a szomszédos síkpárok közé párhuzamos (és egyenlő) kockaélek esnek: és közé , és , közé , továbbá és közé . Ezek a síkpárok tehát egyenlő távolságra vannak egymástól, s így -t 3 egyenlő részre osztják. és tehát valóban az harmadoló pontjaiban állított, egyértelműen meghatározott merőleges síkok. 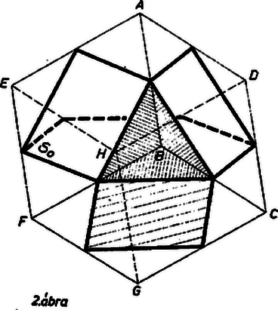 Az -re a felező pontjában állított merőleges sík és közt, velük párhuzamosan és tőlük egyenlő távolságban helyezkedik el, így felezi a kocka
II. Tekintsük előbb a feladat második kérdését. és a kocka felületét az , ill. csúcsban összefutó 3‐3 lapnak -t, ill. -t nem tartalmazó átlóiban metszi. Sorra véve a , , testátlókat merőlegesen harmadoló síkpárokat, és helyén minden kockacsúcs sorra kerül és osztóvonal gyanánt minden lapbeli átló is, éspedig mindegyik kétszer, és más osztóvonal nem lép fel. A lapbeli átlók a kocka 6 lapját 24 egyenlő szárú derékszögű háromszögre darabolják szét. 2‐2 ilyen háromszög átfogója közös, a kocka 1‐1 éle, ami nem osztóvonal, a háromszögpár összefüggő részt alkot, tehát a 4 síkpár a kocka felületét 12 részre osztja. A feladat első kérdésében szerepel, ez a kocka mindegyik lapjából lemetsz egy egyenlő szárú derékszögű háromszöget, amelyben a derékszög csúcsa a lapnak -val, ill. -vel szemben fekvő csúcsa, átfogója pedig az ide befutó oldalak felezőpontjait összekötő szakasz, ezekből a szakaszokból tevődik össze metszésvonala. Sorra véve a további 3 testátló felező merőleges síkjait, és helyén minden kockacsúcs sorra kerül, a kis háromszög derékszögének csúcsa gyanánt ugyancsak, éspedig 3-szor, továbbá átfogó végpontja gyanánt minden él felezőpontja is, 2-szer. Így a kocka mindegyik lapja 4 kis háromszögre és köztük 1 négyzetre oszlik. Az utóbbiaknak a teljes kerülete osztóvonal, ezek tehát a felület különálló részei lesznek. A kis háromszögek viszont 3-asával 1‐1 kockacsúcsban futnak össze, egymáshoz páronként befogójukkal csatlakoznak, ami nem osztóvonal, tehát 3‐3 kis háromszög a kockafelület 1‐1 összefüggő részét alkotja, amelynek határvonalát a 3 átfogó adja. Ezek szerint a kocka felületét a testátlók felező merőleges síkjai 6+8=14 részre osztják fel. Sükösd Csaba (Budapest, József A. g. III. o. t.) Csörnyei Zoltán (Veszprém, Lovassy L. g. IV. o. t.) |