Kezdőlap


Feladat:	1280. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Ajtai Miklós , Bak Zsuzsanna , Bálint L. , Bense Imre , Bódi Z. , Deák I. , Domokos Zsuzsanna , Földes Antónia , Huhn A. , Jahn L. , Laczkovich M. , Langer L. , Lovász L. , Márki L. , Mátrai M. , Nagy Klára , Nagy Péter Tibor , Pelikán József , Siket Aranka , Solti L. , Szabó M. , Székely G. , Sövényházy Mária , Veres F.
Füzet:	1965/január, 9 - 10. oldal		PDF \| MathML
Témakör(ök):	Indirekt bizonyítási mód, Konstruktív megoldási módszer, Szabályos sokszögek által határolt testek, Feladat
Hivatkozás(ok):	Feladatok: 1963/november: 1280. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megpróbáljuk összeállítani egy konvex poliéder modelljét 2 négyzetlapból és szabályos ötszöglapokból, és be fogjuk látni, hogy ez nem lehetséges. Először megállapítjuk a felhasználható ötszöglapok számát.

A poliéder bármelyik csúcsába összefutó lapoknak az illető csúcsnál levő szögei együttvéve nem érhetik el a

360^{\circ}

-ot, különben ugyanis a poliéder nem lenne konvex. Ezért minden csúcsban csak 3‐3 lap futhat össze, mert a szabályos ötszög egy szöge

108^{\circ}

, tompaszög, és így 4 lapot tartalmazó csúcsban a szögek összege nagyobb volna négy derékszögnél.
Legyen az ötszöglapok száma

x

. Így a modell céljára előkészített, különálló lapokon az oldalak és a csúcsok száma egyaranánt

x \cdot 5 + 2 \cdot 4 = 5 x + 8

, és ezek összeállítva

(5 x + 8) / 2

élt és

(5 x + 8) / 3

csúcsot adnak, mert a poliéder minden élét két lap 1‐1 oldala alkotja, és minden csúcsában 3 lapcsúcs egyesül. Így az 1216., ill. az 1175. feladatból¹⁾ ismert EULER‐féle poliédertételt felhasználva, amely szerint konvex poliéderen a lapok és a csúcsok számának összege 2-vel nagyobb az élek számánál:

\begin{matrix} x + 2 + \frac{5 x + 8}{3} = \frac{5 x + 8}{2} + 2, \end{matrix}

ugyanis a lapok száma

x + 2

. Innen

x = 8

, tehát ha létezik a kérdéses poliéder, akkor ötszöglapjainak száma 8.

Ezzel azt is kaptuk, hogy a poliéder csúcsainak száma csak 16 lehet. Közülük legfeljebb 8-ba futhat be négyzetcsúcs, van tehát olyan csúcs, amelyben mind a három lap szabályos ötszög. Nevezzük az ilyeneket

α

-típusú csúcsoknak, és kezdjük az összeállítást egy ilyennel. Könnyű belátni, hogy

α

-típusú csúcs szomszédos csúcsai ugyancsak

α

‐típusúak. Legyen ugyanis

A B

a poliéder egy olyan éle, melyet két ötszöglap alkot (1. ábra I. és II.).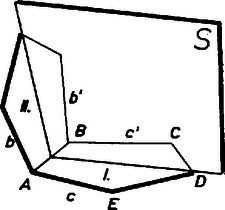

1. ábra

E két lap alakzata szimmetrikus az

A B

él

S

felező merőleges síkjára (a lapok közti szög bármely értéke mellett). Ha tehát az

A

csúcsban a harmadik lap szabályos ötszög, vagyis a

b

c

élek közti szög

108^{\circ}

, akkor ugyanekkora a

b'

c'

élek közti szög is, tehát a

B

-beli harmadik lap is szabályos ötszög, a

B

csúcs

α

‐típusú, amint állítottuk.

Így pedig

α

‐típusú lesz a poliédernek az I. ötszög

C

csúcsából adódó csúcsa, majd a

D

-ből adódó is, és

D

-be a harmadik ötszöglapot beillesztve

E

-ben is 3 ötszöglap fut össze. E 6 ötszöglap alakzatán (2. ábra) további 5 olyan csúcs van, amelyben már 2 lap fut össze, mindegyikük szomszédos a modell egy már elkészült csúcsával, tehát csak

α

‐típusúvá egészíthető ki.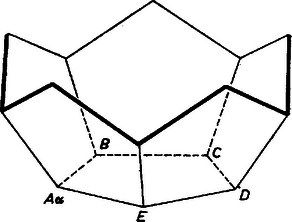

2. ábra

Eszerint az összeállítás egyedül lehetségesnek talált folytatásához egyrészt a megengedettnél több ötszöglapra lenne szükség, másrészt nem nyílik lehetőség az előírt 2 négyzetlap beillesztésére. Így a kérdéses poliéder valóban nem létezik.

Pelikán József(Budapest, Fazekas M. Gyak. G. II. o. t.)

Megjegyzés. Kissé másképpen jutunk ellentmondásra az összeállításban a következő úton. A két négyzetnek csak 2 közös csúcsa lehet, kellene tehát lennie olyan csúcsnak, amelyben 1 négyzet és 2 ötszög fut össze (

β

‐típusú csúcs), legyen ilyen a 3. ábra

A

csúcsa, ahol

E A F

derékszög.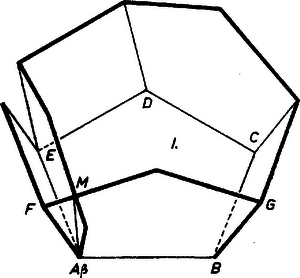

3. ábra

Ekkor viszont a szimmetria miatt

B

β

‐típusú csúcs,

C B G

derékszög, az I. ötszöghöz a

B C

élen is négyzet csatlakozik, ezért a

C D

-n ismét csak ötszög,

D E

-n ismét csak négyzet, végül

E A

-n ismét csak ötszög csatlakozhat, holott abból indultunk ki, hogy itt négyzet csatlakozik.

Bense Imre (Esztergom, Temesvári P. G. IV. o. t.)

2. Az sem lehetséges, hogy a poliéder egy csúcsában 2 négyzet és 1 szabályos ötszög fusson össze (

γ

‐típusú csúcs), mert így az ötszög síkja merőleges a négyzetek közös élére, ugyanígy az ezen él másik végpontjában csatlakozó ötszöglap síkja is, tehát e két ötszöglap síkjai párhuzamosak, úgyszintén további oldalaik is páronként (4. ábra).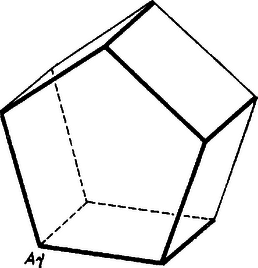

4. ábra

Így az összeállítás csak további négyzetlapokkal folytatható, amit a feladat nem enged meg.

Ajtai Miklós (Budapest, Rákóczi F. G. IV. o. t.)

¹⁾K. M. L. 27 (1963) 117. o., ill. 25 (1962) 134. o.