Feladat:	1278. matematika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bódi Zoltán ,  Deák István ,  Ferenczi György ,  Huhn A. ,  Keresszegi Hajnalka ,  Kiss Katalin ,  Lovász László ,  Mátrai Miklós ,  Nagy Klára ,  Nagy Péter ,  Pelikán József ,  Posta Emil ,  Siket Aranka ,  Szabó Mihály ,  Veres Ferenc
Füzet:	1964/november, 125 - 126. oldal		PDF  |  MathML
Témakör(ök):	Parabola egyenlete, Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1963/november: 1278. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.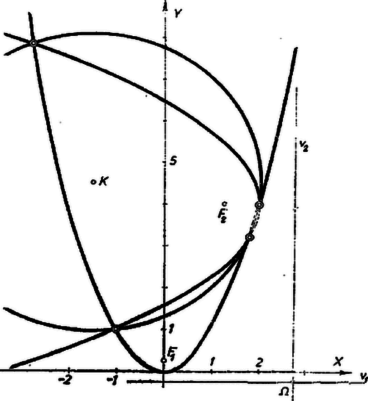     I. Először megmutatjuk, hogy az (1) és (2) paraboláknak $4$ különböző közös pontjuk van. A közös pontok $x$, $y$ koordinátáit a két parabola egyenletének összekapcsolásával nyert egyenletrendszer megoldásai adják. $y$-nak (1)-beli kifejezését (2)-be helyettesítve a közös pontok abszcisszáira a következő egyenletet kapjuk: $\begin{array}{c}{\displaystyle 3\left(x-2\right)+{\left(x^2-4\right)}^2=x^4-8x^2+3x+10=0.}\end{array}$ (3) Vizsgáljuk meg, van-e ennek egész gyöke. Ismeretes, hogy egész együtthatós egyenlet egész gyöke csak az állandó tag osztója lehet. $10$ osztói: $\pm 1$, $\pm 2$, $\pm 5$ és $\pm 10$; közülük $x_1=-1$ és $x_2=2$ kielégítik az egyenletet. A megfelelő $x+1$ és $x-2$ gyöktényezők szorzatát a bal oldalból kiemelve a visszamaradó tényező $x^2+x-5$, tehát a további gyököket az $\begin{array}{c}{\displaystyle x^2+x-5=0}\end{array}$ (4) egyenletből kapjuk. Ennek gyökei valósak és különbözők, mert a diszkrimináns pozitív szám: $21$. $x_1$ és $x_2$ nem gyökei (4)-nek, ezért (3)-nak négy különböző valós gyöke van. (1) szerint a megfelelő ordináták is valósak, tehát az (1) és (2) parabolák egymást valóban négy különböző pontban metszik. A kívánt bizonyításhoz elég megmutatni, hogy van olyan valós kör, melynek egyenletét a metszéspontok koordinátái kielégítik. Írjuk (1)-et így: $\begin{array}{c}{\displaystyle x^2-y=\mathrm{0,}}\end{array}$ ($1a$) és adjuk hozzá (2)-höz. Kellő rendezés után $\begin{array}{c}{\displaystyle x^2+3x+y^2-9y+10={\left(x+\frac{3}{2}\right)}^2+{\left(y-\frac{9}{2}\right)}^2-\frac{25}{2}=0.}\end{array}$ (5) Ez kör egyenlete, középpontja a $\left(-3/2;9/2\right)$ pont, és sugara $5/\sqrt[]{2}$ egységnyi. Másrészt a metszéspontok mindegyike kielégíti (5)-öt, mert bármelyik metszéspont koordinátáit helyettesítve mind ($1a$), mind (2) bal oldalának értéke $0$, tehát az összeadással kapott (5) bal oldalának értéke is $0$. Ezzel a bizonyítást befejeztük. Mint látjuk, nem volt szükség a metszéspontok koordinátáinak kiszámítására és behelyettesítésére.   II. Legyen adva két egymásra merőleges tengelyű parabola. Válasszuk $X$ és $Y$ tengelyeknek az első, ill. a második parabola vezéregyenesét, és legyenek a két fókusz koordinátái $F_1\left(a_1\mathrm{,}{b}_1\right)$, ill. $F_2\left(a_2\mathrm{,}{b}_2\right)$. Így a parabolák csúcsa az $\left(a_1\mathrm{,}{b}_1/2\right)$, ill. az $\left(a_2/\mathrm{2,}{b}_2\right)$ pont, paramétere $b_1$, ill. $a_2$ abszolut értéke, egyenletük: $\begin{array}{c}{\displaystyle {\left(x-a_1\right)}^2-2b_1\left(y-\frac{b_1}{2}\right)=\mathrm{0,}\text{ill.}{\left(y-b_2\right)}^2-2a_2\left(x-\frac{a_2}{2}\right)=0.}\end{array}$ A két parabola közös pontjai mindkét egyenletet kielégítik, tehát kielégítik az ezekből összeadással és rendezéssel adódó $\begin{array}{c}{\displaystyle {\left(x-a_1-a_2\right)}^2+{\left(y-b_1-b_2\right)}^2-2\left(a_1{a}_2+b_1{b}_2\right)=0}\end{array}$ (6) egyenletet is. Ez kör egyenlete, ha a harmadik tag negatív, vagyis $a_1{a}_2+b_1{b}_2>0$, és ekkor $K$ középpontja az $\left(a_1+a_2\mathrm{,}{b}_1+b_2\right)$ pont, sugara $r=\sqrt[]{2\left(a_1{a}_2+b_1{b}_2\right)}$ egység; tehát amennyiben a paraboláknak $4$ (különböző) közös pontjuk van, azok a (6) körön vannak, és így valóban egy húrnégyszög csúcsait adják. Ha pedig $a_1{a}_2+b_1{b}_2\le 0$, akkor nincs a (6)-ot kielégítő pont, ill. egyenlőség esetén egyetlenegy ilyen van, tehát a paraboláknak legfeljebb $1$ közös pontjuk van ‐ a feltevéssel ellentétben. Ezzel az állítás bizonyítását befejeztük.   Lovász László (Budapest, Fazekas M. gyak. g. II. o. t.)   Megjegyzés. A $K$ középpont koordinátáiból látható, hogy az $F_{1}O{F}_{2}K$ négyszög paralelogramma. A koordináta-rendszert az ábráról elhagyva $O$-t a két vezéregyenes metszéspontja adja meg.