Kezdőlap


Feladat:	1272. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Belső László , Földes Antónia , Hadlaczky Éva , Merkel Géza , Palócz András , Szabady Balázs
Füzet:	1964/december, 205 - 207. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Eltolás, Háromszögek nevezetes tételei, Magasságpont, Körülírt kör középpontja, Beírt kör középpontja, Feladat
Hivatkozás(ok):	Feladatok: 1963/október: 1272. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy a $60^{\circ}$ -os szöget bezáró oldalakra merőleges magasságokat a szög felezőjén mint tengelyen tükrözve a bezáró oldalak felező merőlegeseit kapjuk. Ebből már következik, hogy az említett magasságpár metszéspontja, másrészt a felező merőleges-pár metszéspontja ‐ vagyis a magasságpont és a körülírt kör középpontja ‐, egymás tükörképei a $60^{\circ}$ -os szög felezőjére nézve; és így ez a két pont a szögfelező bármely pontjától egyenlő távolságra van, tehát a beírt kör középpontjától is.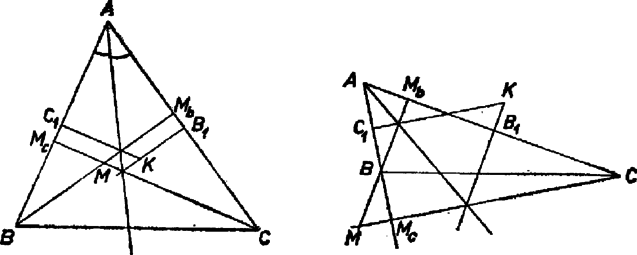

1. ábra

Legyen az

A B C

háromszögben

B A C ∢ = 60^{\circ}

, a magasságpont

M

, a körülírt kör középpontja

K

, az

A B

és

A C

oldalakra merőleges magasság talppontja rendre

M_{c}

M_{b}

, az oldalfelező merőlegeseké pedig rendre

C_{1}

B_{1}

(1. ábra). Így az

A B M_{b}

derékszögű háromszög hasonló egy a tengelyével kettévágott szabályos háromszög egyik feléhez, tehát a

60^{\circ}

-os szög melletti befogója egyenlő az átfogó felével:

A M_{b} = A B / 2 = A C_{1}

. Eszerint az

M_{b}

C_{1}

pontok, továbbá a rajtuk átmenő

M_{b} M

és

C_{1} K

egyenesek valóban tükrösek a

B A C

szög felezőjére nézve. Ugyanígy adódik az

A C M_{c}

háromszögből

A M_{c} = A B_{1}

. Ebből ‐ mint láttuk ‐ következik a feladat állítása.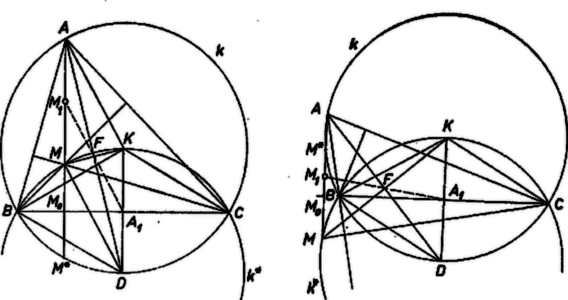

Szabady Balázs (Győr, Révai M. g. III. o. t.)

II. megoldás. Tovább is a fenti jelöléseket használjuk; legyen továbbá a

B A C

szög felezőjének a

k

körülírt körrel való metszéspontja

D

(2. ábra). Bebizonyítjuk, hogy az

A M D K

négyszög rombusz. Így

M

és

K

egymás tükörképei

A D

-re; ebből pedig ‐ mint az I. megoldásban láttuk ‐ következik a feladat állítása.

2. ábra

A M

párhuzamos

K D

-vel, mert az utóbbi is merőleges

B C

-re, hiszen a

D A B

és

D A C

szögek egyenlősége miatt

D

felezi az

A

-t nem tartalmazó

B C

ívet. Fennáll az

A K = K D

egyenlőség is, mert mindkettő a körülírt kör sugara. Elég tehát még az

A M = K D

egyenlőséget bebizonyítanunk. Ehhez megmutatjuk, hogy

B

M

és

K

egy

D

középpontú

k^{x}

körön van. Ebből következik állításunk, mert

k^{x}

sugara,

D K

, egyenlő

k

sugarával, így

D

-t eltolva

K

-ba

k^{x}

átmegy

k

-ba. Az eltoláskor

M

D K

-val párhuzamos

M A

egyenesen mozog, s mivel

k

-ra kerül, annak

A

pontjába kell kerülnie. Így valóban

M A = D K

, az

A M D K

négyszög tehát paralelogramma, amelynek két szomszédos oldala egyenlő, vagyis rombusz.
Azt kell tehát még belátnunk, hogy a

B

M

K

pontokon átmenő

k^{x}

kör egyenlő sugarú

k

-val, középpontja

D

. Ez abból következik, hogy

k^{x}

tükörképe

B C

-re a

k

kör. Ugyanis

B

tükörképe önmaga. A

B K D

szög

60^{\circ}

-os, mert fele a

60^{\circ}

-os

B A C

szöghöz tartozó

B K C

középponti szögnek. Mivel még a

B K

és

D K

körsugarak egyenlők, így a

B K D

háromszög szabályos, tehát a

D K

-ra

B

-ből állított merőleges,

B C

, felezi

D K

-t, vagyis

K

tükörképe

D

. ‐ Belátjuk még, hogy bármely háromszögben a magasságpontnak bármelyik oldalra vonatkozó tükörképe a háromszög köré írt körön van. Ezzel a bizonyítás befejezést nyer, mert

k^{x}

három pontjának a tükörképe

k

egy-egy pontja, tehát a tükörkép egybeesik

k

-val, és

k

középpontja,

K

, a

D

tükörképe, tehát

k^{x}

középpontja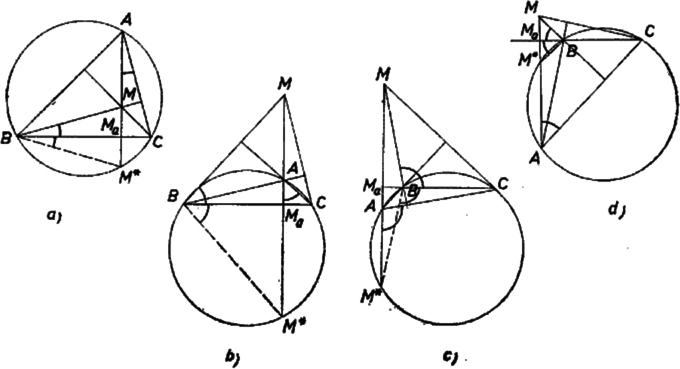

D

3. ábra

A hátralevő állítást így láthatjuk be: jelöljük az

M

magasságpont tükörképét a

B C

oldalra

M^{x}

-gal,

M M^{x}

és

B C

egyenesek metszéspontját

M_{a}

-val. Ha

M_{a}

B C

szakaszon van, akkor ugyanaz a

C M^{x}

ív tartalmazza

A

-t és

B

-t ‐

3 a

) és

b)

ábra ‐, így

M^{x} B C ∢ = M^{x} A C ∢

, mint egy íven nyugvó kerületi szögek, másrészt

M^{x} A C ∢ = C B M ∢

, mint merőleges szárú hegyesszögek. Ha

M_{a}

kívül van a

B C

szakaszon, pl. a

B

-n túli meghosszabbításán, és

A

és

B

ugyanazon az

M^{x} C

íven van ‐

3 c

) ábra ‐, akkor csak annyi változik, hogy az utolsó egyenlőség mindkét szöge tompaszög. Ha az

A

B

és

M^{x}

C

pont párok elválasztják egymást a körön ‐

3 d

) ábra ‐, akkor

M^{x} B M_{a} ∢ = M^{x} A C ∢

, mint az

A M^{x} B C

húrnégyszög külső szöge, és nem mellette fekvő belső szöge, másrészt

M^{x} A C ∢ = M_{a} B M ∢

mivel merőleges szárú hegyesszögek. Így minden esetben

B C

-vel egyenlő szöget bezáró egyenesek metszik ki

M

-et és

M^{x}

-ot egy a

B C

-re merőleges egyenesből, a két pont tehát egymás

B C

-re vonatkozó tükörképe. Ha

M_{a}

pl.

B

-vel egybeesik, akkor

M

és

M^{x}

is ide esik, az állítás nyilván ekkor is igaz.

Hadlaczky Éva (Székesfehérvár, Teleki B. g. IV. o. t.)
Palócz András (Győr, Benedek-rendi Czuczor G. g. III. o. t.)

Megjegyzések. 1. Az

M A = D K

egyenlőséget abból is beláthatjuk, hogy az

M K

szakasz felezőpontja az

A B C

háromszög Feuerbach-körének

F

középpontja (2. ábra), az

M A

és

B C

szakaszok

M_{1}

, ill.

A_{1}

felezőpontjai viszont e kör egy átmérőjének végpontjai. Így

M A ∥ D K

folytán

M_{1} F M Δ ≃ A_{1} F K Δ

, ezért

M A = 2 M M_{1} = 2 K A_{1}

, ez pedig a feltevés folytán egyenlő

K D

-vel.

Merkel Géza és Belső László
(Budapest, XVIII., Hengersor úti g. IV. o. tanulók)

2. Az állítást vektoralgebrai úton is bizonyíthatjuk.

Földes Antónia (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)