Kezdőlap


Feladat:	1269. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Földes Antónia , Komor Tamás , Nagy László
Füzet:	1964/november, 119 - 121. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Vektorok felbontása összetevőkre, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1963/október: 1269. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bizonyítandó egyenlőség fennállását az 1246. feladat II. megoldásában számítással igazoltuk, ezért az alábbiakban számító megoldást nem közlünk.

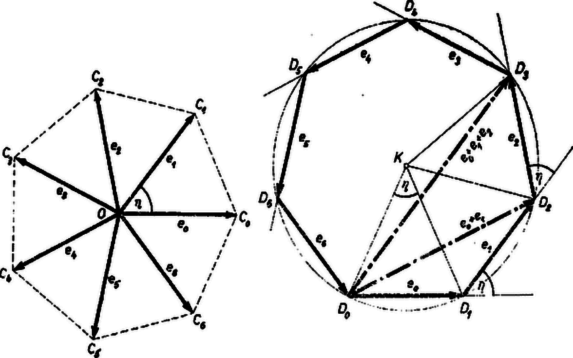
I. megoldás. Írjunk egy egységnyi sugarú körbe egy

C_{0} C_{1} C_{2} C_{3} C_{4} C_{5} C_{6}

szabályos hétszöget és irányítsunk mindegyik csúcsához egy vektort ^{$^{*}$} a kör

O

középpontjából, legyenek ezek

e_{0}, e_{1}, ..., e_{6}

. Megmutatjuk, hogy e vektorok

e

összege a

0

vektor.

Mérjük fel egy

D_{0}

pontból az

e_{0}

-val egyenlő

\vec{D_{0} D_{1}}

vektort, ennek

D_{1}

végpontjából kiindulva a paralelogramma-szabály alkalmazásával az

e_{1}

-gyel egyenlő

\vec{D_{1} D_{2}}

-t,

D_{2}

-ből az

e_{2}

-vel egyenlő

\vec{D_{2} D_{3}}

-t, és így tovább, végül az

e_{5}

-tel egyenlő

\vec{D_{5} D_{6}}

-nak

D_{6}

végpontjából az

e_{6}

-tal egyenlő

\vec{D_{6} D_{7}}

-t. Ekkor

D_{0}

D_{1}

D_{2}

D_{3}

D_{4}

D_{5}

D_{6}

egy szabályos hétszög egymás utáni csúcsai, és

D_{7}

azonos

D_{0}

-lal. Ugyanis a

D_{0} D_{1} D_{2}

háromszög egyenlő szárú, a

D_{0}

-nál és

D_{2}

-nél levő szöge fele a

D_{1}

-nél levő külső szögnek, ez pedig egyenlő az

e_{0}

és

e_{1}

közti szöggel, vagyis a teljes szög hetedrészével, jelöljük ezt

η

-val. Írjunk

k

kört a

D_{0} D_{1} D_{2}

háromszög köré, és legyen ennek középpontja

K

, így a

D_{0} K D_{1}

és

D_{1} K D_{2}

szögek egyenlők

η

-va1, és

K

az az egyetlen pont ^{$^{*}$}, amelyből

D_{0} D_{1}

és

D_{1} D_{2}

látószöge

η

. Meggondolásunkat megismételve

e_{0}

és

e_{1}

helyén

e_{1}

-gyel és

e_{2}

-vel, kapjuk, hogy a

D_{1} D_{2} D_{3}

háromszög körülírt körének középpontja

K

, vagyis

D_{3}

rajta van

k

-n. Ugyanígy haladva tovább

D_{7}

is a

k

-n van, és a

D_{0} K D_{1}, D_{1} K D_{2}, ..., D_{6} K D_{7}

szögek összege

7 η

a teljes szög, így valóban

D_{7} \equiv D_{0}

és

e = e_{0} + e_{1} + ... + e_{6} = \vec{D_{0} D_{7}} = 0

.
Bontsuk fel vektorainkat az

e_{0}

-val megegyező irányú és arra merőleges összetevőkre, ekkor

e_{h}

koordinátái

\begin{matrix} e_{h} (cos \frac{h \cdot 2 π}{7}, sin \frac{h \cdot 2 π}{7}) (h = 0, 1, 2, ..., 6) \end{matrix}

C

csúcsok indexei a pozitív forgás irányában növekszenek).
Az összetevők összege bármely irányra nézve

0

, mert

e=0

-nak bármely irányú összetevője

0

. Írjuk fel ezt az

e_{0}

irányú összetevőkre, és alkalmazzuk a tagokra a

\begin{matrix} cos (x - π) = cos (π - x) = - cos x, cos (2 π - x) = cos x \end{matrix}

azonosságokat:

\begin{matrix} 1 + cos \frac{2 π}{7} + cos \frac{4 π}{7} + cos \frac{6 π}{7} + cos \frac{8 π}{7} + cos \frac{10 π}{7} + cos \frac{12 π}{7} = \\ = 1 + cos \frac{2 π}{7} - cos \frac{3 π}{7} - cos \frac{π}{7} - cos \frac{π}{7} - cos \frac{3 π}{7} + cos \frac{2 π}{7} = \\ = 2 (\frac{1}{2} - cos \frac{π}{7} + cos \frac{2 π}{7} - cos \frac{3 π}{7}) = 0, \end{matrix}

ezért a zárójeles kifejezés

0

, ez pedig éppen a bizonyítandó egyenlőség jobb és bal oldalának különbsége. Ezzel az állítást bebizonyítottuk.

Komor Tamás (Budapest, Fazekas M. gyak. g. II. o. t.)

Megjegyzés. Az

e=0

megállapítást a szimmetriát jobban kihasználva rövidebben kapjuk a következő meggondolással. Vektorrendszerünk az

O

körüli

η

szögű elforgatással önmagába megy át, ezért összegét az eredeti és az elforgatott helyzetben képezve ugyanazt az eredményt kapjuk. Az elforgatott helyzetbeli összeg az eredeti összegből

η

-val való elforgatással adódik, ez csak akkor azonos az eredeti összeggel, ha az összeg

0

, mert a nullvektortól különböző vektort elforgatva, tőle különböző vektort kapunk, hacsak a forgási szög nem egész számú többszöröse

2 π

-nek.

Földes Antónia (Budapest, Apáczai Csere J. g. IV. o. t.)

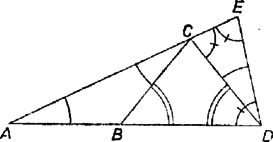
II. megoldás. Mérjük fel egy

ϑ = π / 7

nagyságú szög

A

csúcsától az egyik szárra az

A B = 1

szakaszt, majd jelöljük ki a szárakon váltakozva az előbbiektől mindig különböző

C

D

E

pontokat úgy, hogy álljon

A B = B C = C D = D E

. Ekkor az ábra összes szögeit kifejezhetjük

ϑ

-val, figyelembe véve, hogy az

A B C

B C D

és

C D E

háromszögek egyenlő szárúak, valamint a külső szög tételét alkalmazva az

A B C

és

A C D

háromszögekre:

A C B ∢ = ϑ

;

C B D ∢ = C D B ∢ = 2 ϑ

;

D C E ∢ = D A C ∢ + A D C ∢ = 3 ϑ

(hegyesszög)

= C E D ∢

;

C D E ∢ = ϑ

; végül

A D E ∢ = 3 ϑ

. Ezek szerint, az

A D E

háromszög is egyenlő szárú:

A E = A D

, ill. e szárak részeit az előbbi egyenlő szárú háromszögekből

ϑ

-val kifejezve

\begin{matrix} A C + C E = A B + B D, 2 cos ϑ + 2 cos 3 ϑ = 1 + 2 cos 2 ϑ . \end{matrix}

Innen a bizonyítandó egyenlőség osztással és rendezéssel adódik.

Nagy László (Budapest, I. István g. IV. o. t.)

^{$^{*}$}A vektorokra vonatkozó elemi ismeretek megtalálhatók pl.: Hajós György‐Neukomm Gyula‐Surányi János: Matematikai Versenytételek II. (Tankönyvkiadó, Budapest, 1957) 26‐30. o.

^{$^{*}$}A kisebb $D_{0} D_{1} D_{2}$ szögtartományban.