Feladat:	1267. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Aczél Gábor ,  Berkes István ,  Bóta Károly ,  Deák István ,  Földes Antónia ,  Halász Szilvia ,  Hoffer Anna ,  Horányi Sándor ,  Huhn A. ,  Körner János ,  Langer László ,  Lehel Csaba ,  Lovász László ,  Lux I. ,  Marosi Judit ,  Mátrai Miklós ,  Nagy Klára ,  Nagy Péter Tibor ,  Pelikán József ,  Rejtő Lídia ,  Simonovits András ,  Sófalvi Miklós ,  Székely Gábor ,  Szép András ,  Treer Mária ,  Varga Kornél ,  Veres Ferenc ,  Vesztergombi Katalin
Füzet:	1964/október, 70 - 72. oldal		PDF  |  MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Indirekt bizonyítási mód, Egyéb sokszögek geometriája, Feladat
Hivatkozás(ok):	Feladatok: 1963/október: 1267. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.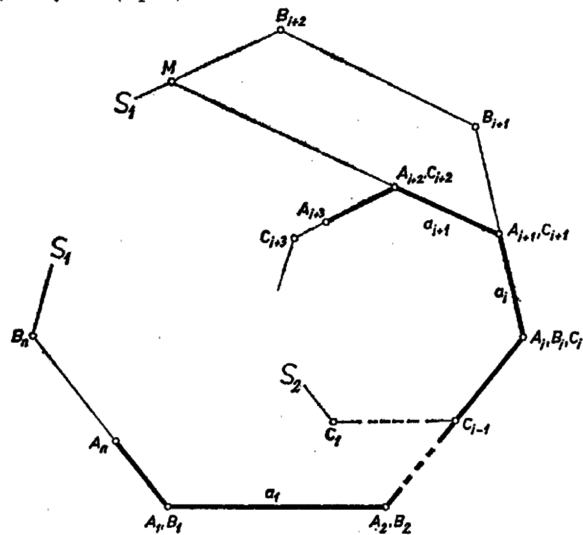     1. ábra   I. megoldás. Ha a kérdéses $n$-szög szögei egyenlők, akkor egyszersmind egyenlők a szabályos $n$-szög szögeivel. Ez viszont a bizonyítandó állítással együtt azt fejezi ki, hogy sokszögünk szabályos $n$-szög. $n=3$ esetére ismeretes, hogy ha egy háromszög mindhárom szöge egyenlő (ti. ${60}^{\circ }$), akkor oldalai is egyenlők, az állítás helyes. Közvetlenül belátható az állítás $n=4$ esetére is. Ekkor derékszögű négyszögről van szó. Ebben a szemben levő oldalak párhuzamosak és egyenlők: $a_1=a_3$ és $a_2=a_4$. (1) szerint viszont $a_2$ nem nagyobb $a-1$-nél, és nem kisebb $a_3$-nál, így $a_2=a_3$, és mind a négy oldal egyenlő. $n\geqq 5$ esetére legyen a kérdéses $n$-szög $A_1{A}_2\text{...}{A}_{n-1}{A}_n=A$, ahol $A_1{A}_2=a_1$, $A_2{A}_3=a_2\mathrm{,}\text{...}$, $A_{n-1}{A}_n=a_{n-1}$, $A_n{A}_1=a_n$, továbbá bármelyik két egymás utáni oldal közti szög $\left(n-2\right){180}^{\circ }/n$, tompaszög. Megmutatjuk, hogy a (2)-vel ellentétes feltevés ellentmondásra vezet. Legyen $a_1\mathrm{,}{a}_2\mathrm{,}\text{...}\mathrm{,}{a}_n$, közül $a_i$ az első olyan, amely határozottan kisebb az előtte állónál: $\begin{array}{c}{\displaystyle a_1=\text{...}=a_{i-1}>a_i\geqq a_{i+1}\geqq \text{...}\geqq a_n\left(i\geqq 2\right)\mathrm{.}}\end{array}$ Tekintsük azt az $a_1$ oldalú $B_1{B}_2\text{...}{B}_n=S_1$ szabályos $n$-szöget, amelynek első két csúcsa azonos $A_1$-gyel, ill. $A_2$-vel, és amely az $A_1{A}_2$ egyenesnek ugyanazon oldalán van, mint $A$. Ekkor $A_1\mathrm{,}{A}_2\mathrm{,}\text{...}{A}_i$ rendre azonos $B_1\mathrm{,}{B}_2\mathrm{,}\text{...}\mathrm{,}{B}_i$-vel, de $A_{i+1}$ már a $B_i{B}_{i+1}$ szakasz közbülső pontja; ebből következik az is, hogy $i<n$, mert különben az $A_{i+1}$ szerepét átvevő $A_l$ nem lehetne azonos $B_1$-gyel. A következő $A_{i+1}{A}_{i+2}$ oldal $S_l$ belsejében van. Ha ugyanis az $A_{i+1}{A}_{i+2}$ egyenesnek $S_l$ kerületével való, $A_{i+1}$-től különböző közös pontja $M$, akkor az $A_{i+1}$-nél és $B_{i+1}$-nél levő szögek egyenlősége miatt az $A_{i+1}{B}_{i+1}{B}_{i+2}M$ négyszög trapéz, benne ‐ mint láttuk ‐ $B_{i+1}$-nél és $B_{i+2}$-nél tompaszög van, ezért $\begin{array}{c}{\displaystyle A_{i+1}M>B_{i+1}{B}_{i+2}=a_1>a_i\geqq a_{i+1}=A_{i+1}{A}_{i+2}\mathrm{.}}\end{array}$ Ebből az is következik, hogy $i<n-1$, mert ha $i=n-1$, akkor $A_{i+2}-n$ $A_1$-et kellene értenünk, de ez nincs $S_1$ belsejében. Ha mármost (1) további részében mindenütt ismét egyenlőség áll: $a_i=a_i+1=\text{...}=a_n$, akkor hasonló meggondolás mutatja, hogy az $A_{i+2}\mathrm{,}{A}_{i+3}\text{...}\mathrm{,}{A}_n$, csúcsok azonosak annak az $a_i$ oldalú $C_1{C}_2\text{...}{C}_n=S_2$ szabályos $n$-szögnek $C_{i+2}\mathrm{,}{C}_{i+3}\mathrm{,}\text{...}\mathrm{,}{C}_n$ csúcsaival, amelynek $C_i{C}_{i+1}$ oldala azonos $A_i{A}_{i+1}$-gyel, és amely az $A_i{A}_{i+1}$ egyenesnek ugyanazon az oldalán van, mint $A$. $S_2$ az $S_1$-nek $a_i:a_1\left(<1\right)$ arányú kicsinyítettje, és $S_1$-gyel hasonló helyzetű a közös $A_i$ csúcsra, mint középpontra nézve. Ezért $C_{i-1}$, $C_i$ és $C_{i+1}$ kivételével $S_2$ minden csúcsa $S_1$ belsejében van. Az $A_n$-nel azonos $C_n$ nincs az $S_1$ kerületén levő 3 csúcs között, mert mint láttuk, $i<n-1$. Azt kaptuk tehát, hogy feltevéseink mellett $A_n$ az $S_1$,-re nézve belső pont. Ez ellentmondásban van azzal, hogy $A$-nak és $S_1$-nek közös csúcsa $A_1$, és így $A_n$ a $B_n{A}_1$ szakaszon van, esetleg ennek $B_n$ végpontjában, mindenesetre $S_1$ kerületén. Ha pedig (1)-nek $a_i$ és $a_n$ közötti részében további határozott egyenlőtlenségek állnának fenn, ebből az előbbi eljárás ismétlésével kapnók, hogy $A_n$ belső pontja egy rendre kisebb oldalú $S_3\mathrm{,}{S}_4\mathrm{,}\text{...}$ szabályos $n$-szögnek, amelyeknek nincs közös csúcsuk $S_1$-gyel, és egészen benne vannak $S_1$-ben ‐ ez pedig ismét ellentmondás azzal, hogy $A_n$-nek $S_1$ kerületén kell lennie, mint fent láttuk. Legfeljebb annyi újabb szabályos $n$-szöget kellene figyelembe vennünk, ahány helyen (1)-ben határozott egyenlőtlenség áll fenn. ‐ Ezzel a bizonyítást befejeztük.    Aczél Gábor (Budapest, Apáczai Csere J. gyak. g. III. o. t.)  dolgozata kiegészítésekkel. 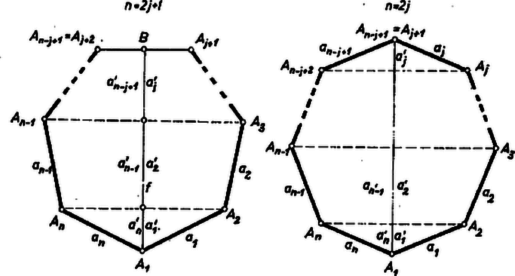    2. ábra   II. megoldás. Továbbra is használva az I. megoldás jelöléseit,az $A$ és $S_1$ $n$-szögek oldalai rendre párhuzamosak egymással. Legyen $n=2j$, ill. $n=2j+1$ aszerint, amint $n$ páros vagy páratlan. Legyen az $A_n{A}_1{A}_2$ szög $f$ felezőjén $A_{j+1}$ merőleges vetülete $B$. Ha $n$ páratlan, akkor $f$ merőleges az $A_{j+l}{A}_{j+2}$ oldalra, így $A_{1}B$ mindkét esetben egyrészt az $A_l{A}_2\text{...}{A}_{j+1}$ törött vonalnak, másrészt az $A_1{A}_n{A}_{n-1}\text{...}{A}_{n-j+1}$ törött vonalnak a vetülete $f$-en, a két vetület különbsége tehát 0. Jelöljük az $a_i$ oldal vetületét $f$-en $a{\text{'}}_i$-vel, ekkor tehát $\begin{array}{c}{\displaystyle \left(a{\text{'}}_1-a{\text{'}}_n\right)+\left(a{\text{'}}_2-a{\text{'}}_{n-1}\right)+\text{...}+\left(a{\text{'}}_j-a{\text{'}}_{n-j+1}\right)=0.}\end{array}$ (3) A két sokszög szögeinek egyenlő voltából következik, hogy az $ak=A_k{A}_{k+1}$ és $a_{n-k+l}=A_{n-k+2}{A}_{n-k+l}$ oldal $\left(k=\mathrm{1,}\mathrm{2,}\text{...}\mathrm{,}j\right)$ ugyanakkora, csak ellenkező irányú ${\phi }_k$ szöget zár be $f$-fel, és a sokszög konvex volta miatt ez a szög hegyes szög, esetleg $0^{\circ }$, ti. ha párhuzamosak. Ezért $\begin{array}{c}{\displaystyle a{\text{'}}_k-a{\text{'}}_{n-k+1}=\left(a_k-a{\text{'}}_{n-k+1}\right)\text{cos}{\phi }_k\geqq \mathrm{0,}}\end{array}$ tehát (3) csak úgy teljesülhet, ha mindegyik különbség 0, így többek közt $a{\text{'}}_1-a{\text{'}}_n=0$, amiből $a_1=a_n$ következik. Ezt (1)-gyel összekapcsolva következik (2).    Nagy Péter Tibor (Kiskunhalas, Szilády Á. g. IV. o. t.)  dolgozata, kiegészítéssel.