Kezdőlap


Feladat:	1264. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Belső László , Császár Z. , Földes Antónia , Gecsey László , Hanák P. , Horányi J. , Kerényi István , Komor Tamás , Laczkovich M. , Langer László , Lehel Csaba , Lovász László , Marosi Judit , Pagony Mária , Pelikán József , Rejtő Lídia , Sófalvi M. , Veres Ferenc , Vesztergombi Katalin
Füzet:	1964/március, 109 - 111. oldal		PDF \| MathML
Témakör(ök):	Diofantikus egyenletek, Kocka, Logikai feladatok, Feladat
Hivatkozás(ok):	Feladatok: 1963/szeptember: 1264. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tartsuk a kockát úgy, hogy egy lapja velünk szemben függőlegesen álljon és jelöljük felső, elülső, alsó, bal, hátsó és jobb lapját rendre $F$ , $E$ , $A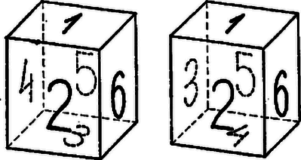$ , $B$ , $H$ , $J$ -vel.

Előírás szerint egymás utáni számokat szomszédos lapokra kell írnunk; a harmadik szám már kerülhet az elsőt tartalmazóval párhuzamos lapra, vagy az előző két számot tartalmazó lap mindegyikével szomszédos helyre. Keressük külön az olyan elrendezéseket, amelyekben három egymás utáni szám az először említett módon helyezkedik el és külön az olyanokat, amelyekben ez nem fordul elő. (Az

1

-et a

6

utáni számnak is tekintjük.)
Ha van három, párhuzamos élekkel csatlakozó lapon három egymás utáni szám, akkor a számokat ugyanannyival megváltoztatva, ha kell, elérhetjük, hogy ez az

1

2

3

legyen, és a kockát forgathatjuk úgy, hogy ezek sorra

F

-en,

E

-n, és

A

-n legyenek ‐ ezt a továbbiakban így fogjuk jelölni:

1 \to F

2 \to E

3 \to A

.
A

4

nem írható

H

-ra, mert akkor az

5

és

6

elhelyezésére a nem szomszédos

B

J

lapok maradnának fenn. A további

4 \to B

és

4 \to J

lehetőségek tükrösek a

B

J

-vel párhuzamos szimmetriasíkra, ezért elég pl. a

4 \to B

lehetőséget vizsgálnunk. Így

B

egyetlen még üres szomszédja

H

, ezért

5 \to H

, és a

6

-os írható a még üres

J

-re, mert

J

szomszédos az

1

-est tartalmazó

F

-fel. Ezek szerint lényegében egyetlen első típusú kockánk van. Ennél az

1 - 6

számokat rendre az

F

E

A

B

H

J

lapra írjuk.
Ha nem lehet három egymás utáni szám párhuzamos élek mentén csatlakozó lapokra írva, akkor az

1

-et,

2

-t ismét

F

E

-re írva

3

B

-re vagy a

J

-re kerülhet. A két lehetőség ismét egymásba vihető a

B

és

J

-vel párhuzamos szimmetriasíkra való tükrözéssel, így elég pl.

3 \to B

-t vizsgálni. Ekkor

4 \to H

nem megengedett, tehát

4

-nek

A

-ra kell kerülnie;

5 \to J

ismét nem megengedett, tehát

5

-nek

H

-ra és

6

-nak

J

-re kell kerülnie. Ez megfelelő elrendezés, mert az

1

-et tartalmazó

F

szomszédos

J

-vel és az

5

-öt tartalmazó

H

-val is, továbbá

J

szomszédos a

2

-t tartalmazó

E

-vel is. Így második típusú elrendezés is lényegében egy van csak, az

1 - 6

számok itt az

F

E

B

A

H

J

lapokra kerülnek.
Ezzel a feladatnak

2

megoldását találtuk, és ezek a megkülönböztetésükre használt tulajdonság miatt egyik megengedett átalakítással sem vihetők egymásba.

II. megoldás. A kocka lapjait a felírt számok sorrendjében bejárva és a bejárást egyszer megismételve bármelyik lapról kiindulva a szemben levő lapra vagy

2

, vagy

3

, vagy

4

lépésben jutunk el ‐ mert

1

lépés után is szomszédos lapon vagyunk és

5

lépés után is ‐, az átellenes lapról a kiindulási lapra vissza pedig rendre

4

3

, ill.

2

lépésben, mert egy lapról ugyanoda

6

lépés után érünk vissza. Így

2

párhuzamos lap rövidebb távolsága a bejárás mentén csak

2

, vagy

3

lépés lehet.
Jellemezzük a feladatnak megfelelő elrendezéseket, mint bejárásokat úgy, hogy megadjuk a kocka

3

párhuzamos lap-párjának a bejárás menti távolságát. Ekkor a következő négy távolsághármas jöhet számításba:

\begin{matrix} 2, 2, 2; 2, 2, 3; 2, 3, 3; 3, 3, 3. \end{matrix}

(Az egyes számhármasokon belül a sorrend lényegtelen.)
Jelöljük a

3

távolságot

t_{1}

t_{2}

t_{3}

-mal, legyenek a

t_{1}

távolságra levő lapokon az

a

b

számok, a

t_{2}

távolságra levő lapokon

c

és

d

, a

t_{3}

-ra levőkön

e

és

f

. Ekkor a

b - a

d - c

f - e

különbségek

t_{1}

t_{2}

t_{3}

-mal egyeznek meg, vagy azoktól

6

valamilyen többszörösével térnek el. Másrészt

a

b

c

d

e

f

között

1

-től

6

-ig mindegyik szám előfordul és csak egyszer. Így egyrészt

\begin{matrix} b - a + d - c + f - e = t_{1} + t_{2} + t_{3} + 6 \cdot k, \end{matrix}

ahol

k

valamilyen egész szám, másrészt

\begin{matrix} b - a + d - c + f - e = a + b + c + d + e + f - 2 (a + c + e) = \\ = 1 + 2 + 3 + 4 + 5 + 6 - 2 (a + c + e) = 21 - 2 (a + c + e), \end{matrix}

tehát a három különbség összege páratlan, s így páratlannak kell lennie a három távolság összegének is. A négy lehetőség közül az első és a harmadik tehát nem fordulhat elő.
A második típusú elrendezés

3

egységnyi távolságban levő lap-párjára

1

-et és

4

-et írva ‐ a további számok lehetséges párosításai és különbségeik:

\begin{matrix} a 2, 3és5, 6párosítás különbségei: 1és1, \end{matrix}

\begin{matrix} a 2, 5és3, 6párosítás különbségei: 3és3, \end{matrix}

\begin{matrix} a 2, 6és3, 5párosítás különbségei: 4és2, \end{matrix}

a harmadik párosítás megfelelő. Ebből

1

bejárást kapunk, mert

1 \to F

4 \to A

rögzítése után a kocka függőleges tengelye körüli forgatással ‐ ha szükséges ‐ a

2

-t

E

-re hozhatjuk, így

6 \to H

, és a

3

5

számpárnak a

B

J

lappáron levő kétféle elhelyezése tükrös a

B

J

lap-pár szimmetria síkjára.
Negyedik típusú bejárás is van ‐ éspedig lényegében

1

‐ mert az

1

4

;

2

5

és

3

6

párosítás különbségei

3

3

és

3

.
A képezésből nyilvánvaló, hogy e két megoldás sem szimmetriával, sem a számoknak a bejárási útvonal mentén való eltolásával nem vihető át egymásba.

Gálfi László, megoldás-feldolgozó