Feladat: 1262. matematika feladat Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Császár Zoltán 
Füzet: 1964/március, 108 - 109. oldal  PDF  |  MathML 
Témakör(ök): Magasságvonal, Hozzáférhetetlenségi szerkesztések síkban, Síkbeli szimmetrikus alakzatok, Feladat
Hivatkozás(ok):Feladatok: 1963/szeptember: 1262. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Elég módot mutatnunk a háromszög egyik magasságvonalának megszerkesztésére, ezt az eljárást csupán ismételnünk kell. A harmadik magasságvonalat már az első kettő metszéspontja gyanánt kiadódott magasságpontnak a csúccsal való összekötésével is megkaphatjuk, hacsak a magasságpont nem esik egybe a csúccsal. ‐ Elég az is, ha valahol a síkon egy n merőlegest szerkesztünk a háromszög elsőnek kiválasztott a oldalára, mert így már csak párhuzamost kell húznunk n-nel a szemben fekvő csúcson át. A merőleges megszerkesztéséhez használhatjuk fel az adott kört.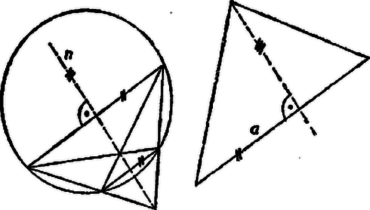

 
 
1. ábra
 

Húzzunk a körben két az oldallal párhuzamos húrt, ezek végpontjai egy szimmetrikus trapéz csúcsait adják. Egyrészt húzzuk meg ennek átlóit, másrészt hosszabbítsuk meg szárait a metszéspontjukig. Az átlók metszéspontját a szárak metszéspontjával összekötve megkapjuk a trapéz szimmetria-tengelyét, ez merőleges a párhuzamos oldalakra. Ezzel a feladatot megoldottuk.
Előfordulhat, hogy a szárak kicsi szöget alkotnak, és így metszéspontjuk távol esik. Bár szerkesztések elvi megoldásában a méretekre nem vagyunk tekintettel, vehetünk ilyen esetben a felvett húrok egyike helyett más, kedvezőbb párhuzamos húrt. ‐ Ha pedig tudjuk, hogy a két szár párhuzamosnak adódott ‐ vagyis trapézunk téglalap ‐, akkor már a szár merőleges a kiszemelt oldalra.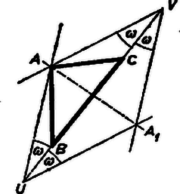
 
 Császár Zoltán (Budapest, Bláthy O. erősár. ip. techn. III. o. t.)
 
Megjegyzések. 1. A trapéz megszerkesztett szimmetriatengelye az adott körben átmérő. Még egy átmérő az előbbit a kör középpontjában metszi. A középpontot ismerve bármely húrra a végpontjában Thalész tétele alapján is megszerkeszthetjük a merőlegest.
 
2. Székely Jenő egyetemi hallgató, lapunk volt versenyzője megjegyezte, hogy ha a szögvonalzót úgy értjük, hogy adott egyenessel adott ω közelebbről meg nem határozott szöget bezáró egyenes szerkeszthető, akkor a kör nem szükséges. Pl. az A csúcsból húzott magasságot megszerkeszthetjük úgy, hogy A-n át megszerkesztjük azt az AU, ill. AV egyenest, amelyek a BC, ill. CB iránnyal ω szöget zárnak be. Ha a két egyenes egybeesik, akkor az adott szög derékszög, és megkaptuk a magasságot; ha nem, akkor U-n, ill. V-n át a BC, ill. CB iránnyal, a BC egyenes A-t nem tartalmazó oldalán ω szöget bezáró egyenest szerkesztünk. Ezek A1 metszéspontja az A pont tükörképe a BC egyenesre, így AA1 az A-ból húzott magasság egyenese (2. ábra).
 
 
2. ábra
 

Ha pedig a szögvonalzót úgy értelmezzük, hogy tetszés szerinti iránnyal párhuzamos szerkeszthető vele, a kört akkor is egy adott irány (pl. AC) BC-re vonatkozó tükörképének megszerkesztésére használja és azzal végzi az előbbi szerkesztést. Így a következő szerkesztés adódik:
Messe egy AC-vel párhuzamos egyenes a kört a P és Q pontban, a P-n és Q-n át BC-vel párhuzamosan húzott egyenes pedig másodszor a P1, ill. Q1 pontban. Húzzunk A-n és C-n át párhuzamost P1Q1-gyel, majd az előbbinek a BC egyenessel való U metszéspontján át párhuzamost PQ-val. Messe ez a C-n át rajzolt egyenest A1-ben. Az A1CU háromszög az ACU háromszög tükörképe a BC egyenesre, s így AA1 az A-ból húzott magasság egyenese, ugyanis PP1QQ1 vagy PP1Q1Q szimmetrikus trapéz, így ACU∢=QPP1∢=Q1P1P∢=A1CU∢ é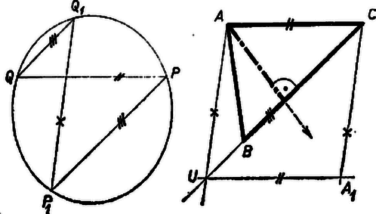s AUC∢=Q1P1P∢=QPP1∢=A1UC∢, vagy ACU∢=PQQ1∢= =P1Q1Q∢=A1CU∢, és AUC∢=P1Q1Q∢=PQQ1∢=A1UC∢ (3., ill. 4. ábra).
 
 
3. ábra
 
 
4. ábra