Kezdőlap


Feladat:	1261. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csirik János , Horváth József , Mezey István , Nagy Péter Tibor , Radó András
Füzet:	1965/május, 198 - 202. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Tengelyes tükrözés, Eltolás, Derékszögű háromszögek geometriája, Körülírt kör, Körök, Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek szerkesztése, Feladat
Hivatkozás(ok):	Feladatok: 1963/szeptember: 1261. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen $A B C$ a keresett háromszög, $a = B C$ , $b = A C$ a befogók, $c = A B$ az átfogó. Mérjük rá a befogók meghosszabbítására az $A B_{1} = B A_{1} = c$ távolságót (1. ábra). Ekkor az $A_{1} B_{1} C Δ$ befogói $A_{1} C = a + c = p$ , $B_{1} C = b + c = q$ a megadott távolságok. Így a feladatot a következővé alakítottuk át: Szerkesszük meg adott $A_{1} B_{1} C Δ$ $A_{1} C$ és $B_{1} C$ oldalán a $B$ és $A$ pontot úgy, hogy az $A_{1} B A B_{1}$ törött vonal egyenlő szakaszokból álljon. Ez a feladat többféleképpen is megoldható.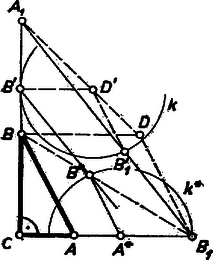

1. ábra

a) A

B

-ből

A B_{1}

-gyel és

B_{1}

-ből

A B

-vel párhuzamosan húzott egyenesek metszéspontja legyen

D

, ekkor az

A_{1} B D B_{1}

törött vonal is egyenlő szakaszokból áll, és első két szakasza

A_{1} C

-vel és

C B_{1}

-gyel párhuzamos. Ehhez hasonlót a szerkeszthetünk úgy, hogy

A_{1} C

-re

A_{1}

-ből tetszés szerinti

A_{1} B'

távolságot mérünk;

B'

-ből

A_{1} C

-re merőlegesen annak

B_{1}

-et tartalmazó partján felmérjük a

B' D' = A_{1} B'

távolságot; a

D'

körül

D' B'

sugárral rajzolt körnek az

A_{1}

-től távolabbi metszéspontja

A_{1} B_{1}

-gyel legyen

B'_{1}

D

-t az

A_{1} D'

és a

B_{1}

-ből induló,

B'_{1} D'

-vel párhuzamos egyenes metszéspontja adja; végül

B

-t a

D

-n át

B_{1} C

-vel párhuzamosan húzott egyenes metszi ki

A_{1} C

-ből,

A

-t pedig a

B_{1}

középpontú

B_{1} D

sugarú kör a

B_{1} C

szakaszból.
Világos, hogy a megszerkesztett törött vonal egyenlő szakaszokból áll, s így az

A B C Δ

megfelel a feladat kirovásainak, feltéve, hogy

A

és

B

C B_{1}

és

C A_{1}

oldalon keletkezik. A szerkesztés változatlanul végrehajtható, ha a

C

-nél levő

γ

szög adott, de derékszögtől különböző (2. ábra). Nem alkalmazható, ha

D

(és

D'

) az

A_{1} B_{1}

egyenesre esik, azaz ha az

A_{1} B_{1} C Δ

egyenlő szárú,

p = q

. Ekkor azonban az

A B D B_{1}

rombusz átlója, amely felezi az

A B_{1} D

szöget, egyben az

A_{1} B_{1} C

szög felezője is, tehát ez metszi ki

B

-t

A_{1} C

-ből, továbbá ez esetben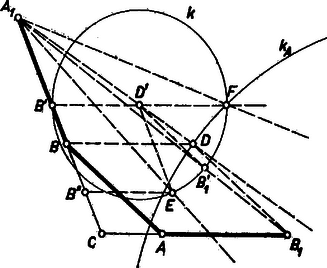

A B ∥ A_{1} B_{1}

2. ábra

D' B'_{1}

-vel párhuzamos

B A

irány az

A_{1} C

és

C B_{1}

irány közé esik; így

B'_{1}

-nek az ezekkel párhuzamos sugarak alkotta

E D' F

konvex (

B'

-t nem tartalmazó) szögtartományban kell lennie, akkor keletkezik

A

és

B

a megfelelő oldalszakaszokon. Jelöljük az

E

-ből

B_{1} C

-vel párhuzamosan húzott egyenes és

A_{1} C

metszéspontját

B''

-vel. Ekkor a mondott feltétel azzal ekvivalens (mivel

B'_{1}

A_{1} B_{1}

egyenesen van), hogy

p / q = A_{1} C / B_{1} C

A_{1} B' / B' F = 1 / 2

és

A_{1} B'' / B'' E = 2

értékek közé essék (ugyanis

A_{1} B'' = A_{1} B' + B' B'' = A_{1} B' + D' E = 2 A_{1} B'

). A szerkeszthetőség feltétele tehát, hogy

q / 2 < p < 2 q

legyen, más szóval az adott szakaszok közül, ha nem egyenlők, a nagyobbik kisebb legyen a kisebbik kétszeresénél.
b) Az előbbi megoldás jelöléseit megtartva, de nem szorítkozva derékszögű háromszögre

A_{1} D = 2 A_{1} B sin (γ / 2) = 2 B_{1} D sin (γ / 2)

. A

D

pont

A_{1}

-től és

B_{1}

-től mért távolságának aránya eszerint

2 sin (γ / 2)

D

tehát az ennek megfelelő Apollóniosz-féle kör és az

A_{1}

-ből induló,

A_{1} C

-vel

90^{\circ} - γ / 2

szöget bezáró félegyenes metszéspontja. Tovább az előző megoldáshoz hasonlóan járhatunk el.

γ = 60^{\circ}

esetében az Apollóniosz-kör helyébe a

B_{1} A_{1}

szakasz felező merőlegese lép.
A szerkesztés helyessége az elemzés gondolatmenetének megfordításával könnyen belátható. A szerkeszthetőség feltételének megállapítását az olvasóra bízzuk.
c) A

D

pont segítségül vétele nélkül is megszerkeszthető az

A_{1} B A B_{1}

törött vonal. Mérjük fel

A_{1} C

-re és

B_{1} C

-re az egyenlő

A_{1} B'

és

B_{1} A^{*}

távolságot, húzzuk meg az

A^{*}

középpontú és

A^{*} B_{1}

sugarú

k^{*}

körnek azt a felét, amelyik a

B_{1} C

egyenes

A_{1}

-et tartalmazó partján fekszik, majd toljuk el

A_{1} B'

-t párhuzamosan

A_{1} B_{1}

mentén úgy, hogy

B'

a félkörre essék. A pont új

B^{*}

helyzetét a

B'

-ből

A_{1} B_{1}

-gyel párhuzamosan húzott egyenes metszi ki a félkörből.

B

-t a

B_{1} B^{*}

egyenes metszi ki

A_{1} C

-ből,

A

-t pedig a

B

-n át

B^{*} A^{*}

-gal párhuzamosan húzott egyenes

B_{1} C

-ből.
A szerkesztés helyessége könnyen látható, igazolását (ami az a) esethez hasonlóan végezhető) az olvasóra hagyjuk.
Csirik János (Orosháza, Táncsics M. G.)
Horváth József (Esztergom, Temesvári Pelbárt G.)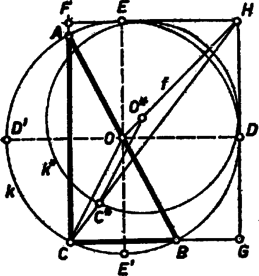

3. ábra

II. megoldás. A következő megoldás kihasználja, hogy

γ = 90^{\circ}

. Az adott szakaszok felét közvetlenül megtaláljuk 3. ábránkban, ha vesszük a keresett

A B C

háromszög köré írt

k

kört és ennek az

A C

és

B C

befogókra merőleges

D D'

, ill.

E E'

átmérőjét (

D

és

E

C

-t nem tartalmazó

A B

íven). Ugyanis a derékszögű háromszög köré írt kör sugara

c / 2

, középpontjának,

O

-nak távolsága az

A C

és

B C

befogóktól

a / 2

, ill.

b / 2

, ezért

D

távolsága

A C

-től

(a + c) / 2

E

távolsága

B C

-től

(b + c) / 2

.
Tekintsük most azt a téglalapot, amelynek oldalegyenesei egyrészt az

A C B

derékszög szárai, másrészt az ezekkel

D

-n, ill.

E

-n át húzott párhuzamosok. A

k

kör ennek utóbbi két oldalát érinti és átmegy az érintett oldalak közös végpontjából kiinduló átló másik végpontján.
Ezekből a következő szerkesztés adódik: Az adott szakaszok feléből megszerkesztjük a

C G H F

téglalapot (

C G = p / 2

C F = q / 2

), meghúzzuk a

H C

átlót és az

F H G

derékszög

f

felezőjét.

f

-nek egy tetszés szerinti

O^{*}

pontja körül a

H F

egyenest érintő

k^{*}

kört írunk, ennek a

H C

egyenessel való,

H

-tól távolabbi metszéspontja

C^{*}

. A

C

-n átmenő,

C^{*} O^{*}

-gal párhuzamos egyenesnek

f

-fel való

O

metszéspontja körül

O C

sugárral írt körből az

F C

G C

egyenes kimetszi

A

-t, ill.

B

-t.
Ha

C^{*}

-nak

G H

-tól mért távolsága kisebbnek adódik, mint

k^{*}

sugara, vagy ha egyenlő vele, akkor az adódó

O

-t

C F

elválasztja

D

-től,

B

G C

meghosszabbításán keletkezik, és az

A B C Δ

-ben

A B - B C = p

A B + A C = q

. (Hasonló áll az előző megoldásokban is, ha a szerkeszthetőség feltétele nem teljesül, azzal a kiegészítéssel, hogy a megszerkesztett háromszögben

γ

helyén a kiegészítő szöge lép fel.)
A szerkesztés nem hajtható végre, ha

p = q

, mert így

O

és

O^{*}

C H

átlón van; viszont ekkor

D C H ∢ = 22, 5^{\circ}

, és ez ad módot a szerkesztésre.
Nagy Péter Tibor (Kiskunhalas, Szilády Á. G.)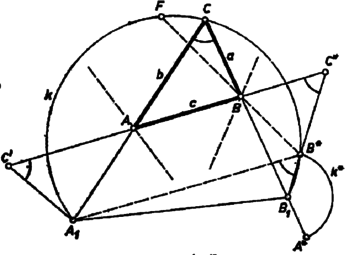

4. ábra

III. megoldás. A következő megoldás bonyolultabb az előzőknél, viszont még hasonlóságot sem használ fel. Tükrözzük a keresett

A B C Δ

-et az

A

és a

B

csúcsnál levő külső szög felezőjére, és legyen a tükörkép

A A_{1} C'

, ill.

B_{1} B C''

(4. ábra). Az

A_{1}

csúcs

C A

B_{1}

pedig

C B

meghosszabbításán van,

C A_{1} = C A + A B = b + c = q

C B_{1} = a + c = p

, továbbá

C'

és

C''

A B

meghosszabbításain vannak,

A_{1} C' C'' ∢ = B_{1} C'' C' ∢ = A_{1} C B_{1} ∢ = γ

, és

C'' B_{1} = C A = b

. Messe az

A_{1}

-en átmenő,

A B

-vel párhuzamos egyenes

C'' B_{1}

-et

B^{*}

-ban. Így

A_{1} B^{*} C'' C'

szimmetrikus trapéz,

C'' B^{*} = C' A_{1} = C B = a

B^{*} B_{1} = C'' B_{1} - C'' B^{*} = b - a = q - p = C A_{1} - C B_{1}

végül

A_{1} B^{*} B_{1} ∢ = C' C'' B_{1} ∢ = γ

. A

q > p

(vagyis

b > a

) feltevés miatt

A_{1} B^{*}

elválasztja

B_{1}

-et

C''

-től, és így

C

-től is, ezért

B^{*}

A_{1} B_{1} C Δ

köré írt

k

körnek

C

-t tartalmazó

A_{1} B_{1}

ívén van. Ezek alapján az

A B C Δ

megszerkesztése a következő.
Egy

C

csúcsú,

γ

nagyságú szög száraira fölmérjük

C A_{1} = C A^{*} = q

szakaszt, a második szárra

C B_{1} = p

-t is. Megrajzoljuk

k

-t, és ennek mondott ívét metsszük a

B_{1}

körüli,

B_{1} A^{*} = q - p

sugarú

k^{*}

körrel, a metszéspont

B^{*}

. Az

A_{1} B_{1} B^{*} Δ

B^{*}

-ból kiinduló külső szögfelezője

C B_{1}

-ből kimetszi

B

-t, végül a

B

-n átmenő,

A_{1} B^{*}

-gal párhuzamos egyenes

C A_{1}

-ből

A

-t.
Az

A B C Δ

megfelel a követelményeknek. Legyen

A B

és

B_{1} B^{*}

metszéspontja

C''

, továbbá

C'

A B

-nek

A

-n túli meghosszabbításán az a pont, amelyre

A_{1} C' A ∢ = γ

. Ugyanekkora a

B_{1} B^{*} A_{1} ∢

és a vele egyállású

B_{1} C'' B ∢

, ezért, valamint az

A

-nál és

B

-nél levő csúcsszögek miatt az

A B C

A A_{1} C'

és

B_{1} B C''

háromszögek két-két megfelelő szöge egyenlő. Az utóbbi két háromszög egybevágó, mert ezeken felül egy-egy megfelelő oldaluk egyenlő, ugyanis a végzett szerkesztések miatt

B^{*} B C''

egyenlő szárú háromszög,

A_{1} B^{*} C'' C'

pedig egyenlő szárú trapéz, így valóban

A_{1} C' = B^{*} C'' = B C''

. Eszerint

A A_{1} = B_{1} B

. Egyenlő továbbá az előbbi első és utolsó háromszög két-két megfelelő oldalának különbsége:

\begin{matrix} C A - C B = C A_{1} - A A_{1} - C A^{*} + B A^{*} = B B_{1} + B_{1} A^{*} - A A_{1} = \\ = B_{1} B^{*} = B_{1} C'' - B^{*} C'' = B_{1} C'' - B C'', \end{matrix}

eszerint

A B C Δ ≃ B_{1} B C'' Δ ≃ A A_{1} C' Δ

. Ennélfogva az

A B C Δ

-ben

\begin{matrix} C A + A B & = C A + A A_{1} = C A_{1} = q, \\ C B + B A & = C B + B B_{1} = C B_{1} = p, \end{matrix}

végül az

A C B ∢

az előírt

γ

nagyságú. Ezeket kellett bizonyítanunk.
A felhasznált

B^{*} B

szögfelező

k

-ból a

C

-t tartalmazó

A_{1} B_{1}

ív

F

felezőpontján át lép ki, másrészt

q > p

miatt

F

a mondott ív

C A_{1}

rész-ívén van. Ezért

B

akkor és csak akkor adódik a

C B_{1}

szakasz belsejében, ha

B^{*}

B_{1} C

íven adódott. Ennek feltétele

B_{1} B^{*} < B_{1} C

q - p < p

, azaz

p < q < 2 p

. Ekkor

A

C A_{1}

szakaszon adódik, mert az

A B

egyenes elválasztja

C

-t

A_{1} B^{*}

-tól.
Ebben a szerkesztésben sem használtuk ki, hogy

γ

derékszög. Ha

γ = 90^{\circ}

, akkor

A_{1} B^{*} = C' C'' = a + b + c

.
Mezey István (Debrecen, Fazekas M. G.)

Megjegyzés.

p = q

esetén a szerkesztés nem alkalmazható, mert

B^{*} = B_{1}

IV. megoldás. Könnyen célhoz érhetünk számítás segítségül vételével. A

c + a = p

c + b = q

a^{2} + b^{2} = c^{2}

egyenletrendszerből

c = p + q - \sqrt[]{2 p q}

(a másodfokú egyenlet másik gyöke nem felel meg, mert

p + q = c + (a + b + c) > c

). Eszerint

b = \sqrt[]{2 p q} - p

, vagyis

2 p

és

q

mértani középarányosából

p

-t kivonva a

b

befogót,

q

kivonásával

a

-t kapjuk. A kapott eredmény

b + p = a + b + c = \sqrt[]{2 p q}

alakban is írható, ezért a kivonásokat a mértani középpel egyenlő szakasz két vége felől végezve, középső szakaszként megjelenik az átfogó (5. ábra).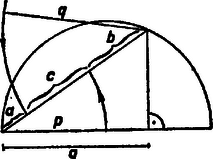

5. ábra

Radó András (Győr, Benedek-rendi Czuczor G. G.)

Megjegyzések. 1. A szerkesztés átvihető tetszés szerinti

γ

szögre, Pythagoras tételét a koszinusz-tétellel helyettesítve.
2. Az utoljára nyert összefüggés szerint derékszögű háromszög oldalaira mindig fennáll:

\begin{matrix} {(a + b + c)}^{2} = 2 (a + c) (b + c), \end{matrix}

ahol

c

az átfogó. Hasonlóan

\begin{matrix} {(a + c)}^{2} + {(b + c)}^{2} + {(a + b + c)}^{2} = \\ = {[(a + c) + (b + c)]}^{2} . \end{matrix}

A III. megoldásnak derékszögű háromszögre való alkalmazása az

\begin{matrix} {(a + b + c)}^{2} + {(b - a)}^{2} = {(a + b + c)}^{2} + {[(b + c) - (a + c)]}^{2} = \\ = {(a + c)}^{2} + {(b + c)}^{2} \end{matrix}

azonossággal egyértelmű. Ezek az összefüggések egy-egy lehetőséget adnak

a + b + c

megszerkesztésére, abból pedig

a

b

és

c

már könnyen nyerhető.