| Feladat: | 1255. matematika feladat | Korcsoport: 18- | Nehézségi fok: átlagos |
| Megoldó(k): | Bálint Lajos , Berecz Ágota , Csirik J. , Érdi B. , Fodor Zs. , Folly G. , Földes Antónia , Gálfi I. , Hirka A. , Hoffmann P. , Kiss A. , Komor T. , Kőszegi L. , Lénárt Z. , Malatinszky G. , Marosi Judit , Minárik L. , Pelikán J. , Ringler A. , Somos P. , Szalkai I. , Szilágyi T. , Tamás E. , Tamás G. , Treer Mária , Veres F. | ||
| Füzet: | 1964/március, 106 - 107. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Csonkagúlák, Terület, felszín, Térfogat, Héroni számhármasok, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1963/május: 1255. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az oldallapok az adott alaplappal tompaszöget zárnak be, ezért az adott alaplap a csonkagúla kisebb alaplapja, tehát ez az alaplapja a test kiegészítő gúlájának. Ennek magasságát tudjuk a hajlásszögek egyenlőségéből könnyen meghatározni. Ezzel ismerjük a két alaplap arányát is. A kisebb alap területét Heron képletével számíthatjuk ki; a nagyobb területére , . E gúla oldallapjai az adott szög kiegészítő szögével, -kal hajlanak az alaphoz. Ebből következik, hogy egyenlők egyrészt a kiegészítő gúla oldalmagasságai is, másrészt ezeknek az alapon levő vetületei; ugyanis ezen szakaszok között mérhetjük az oldallapok hajlásszögét, és a keletkező három derékszögű háromszögben a testmagasság közös befogó, és a vele szemben levő szögek az egyenlő lapszögek, tehát a háromszögek egybevágók. 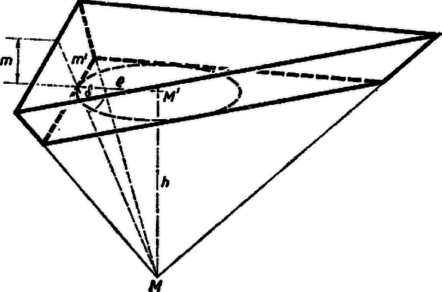 Ezek szerint a kiegészítő gúla főcsúcsának az alapon levő vetülete egyenlő távol van az alapháromszög oldalaitól, továbbá benne van a háromszögben, tehát azonos az alapháromszögbe írt kör középpontjával, a távolságok közös hossza pedig egyenlő a beírt kör sugarával. -t az oldalakból ismert módon kiszámolhatjuk, ebből pedig megkapjuk a kiegészítő gúla magasságát. Mindjárt numerikusan: Így (Legfeljebb Nyilvánvaló, hogy az oldallap trapézok végül a csonkagúla felszíne Bálint Lajos (Budapest, Fáy A. Gimn., III. o. t.) |