Kezdőlap


Feladat:	1254. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Antal Magdolna , Bak Zsuzsanna , Berecz Ágota , Csirik J. , Csörnyei Z. , Érdi Bálint , Folly Gábor , Földes Antónia , Gálfi István , Gyárfás András , Hirka A. , Hoffmann P. , Horváth J. , Komor Tamás , Kőszegi László , Lehel Jenő , Lénárt Zoltán , Lovász László , Makai Endre , Malatinszky G. , Nagy Klára , Nagy Mária , Nárai György , Pelikán József , Sófalvi M. , Somogyi István , Somos Péter , Szalkai István , Székely Gábor , Szemere J. , Szepesvári György , Szidarovszky Ferenc , Szilágyi Tivadar , Tamás Endre , Tamás G. , Treer Mária
Füzet:	1964/április, 153 - 156. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus egyenletek, Trigonometria, Szinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1963/május: 1254. matematika feladat

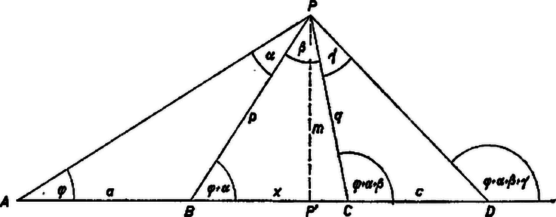
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Először a $P A D = φ$ szöget számítjuk ki. Vezessük be a következő jelöléseket: $A B = a$ , $B C = x$ , $C D = c$ ; $P$ -ből mért látószögük rendre $α$ , $β$ , $γ$ , $α + β + γ = δ$ , továbbá $P B = p$ és $P C = q$ . Ezekkel a $P A B$ , $P B C$ , $P C D$ háromszögből a szinusz‐tétel alapján

\begin{matrix} \frac{a}{p} = \frac{sin α}{sin φ}, \frac{p}{q} = \frac{sin (φ + α + β)}{sin (φ + α)}, \frac{q}{c} = \frac{sin (φ + δ)}{sin γ} . \end{matrix}

(1)

A három egyenlőség bal, ill. jobb oldalainak összeszorzásával adódó egyenletből

p

és

q

kiesik, a fellépő adatok közül csak

φ

ismeretlen. Más szóval: egyismeretlenes egyenletet kapunk

φ

-re:

\begin{matrix} \frac{a}{c} = \frac{sin α sin (φ + α + β) sin (φ + δ)}{sin γ sin φ sin (φ + α)}, \end{matrix}

(2)

amiből

\begin{matrix} \frac{sin (φ + α + β) sin (φ + δ)}{sin φ sin (φ + α)} = \frac{a sin γ}{c sin α} = k, \end{matrix}

ismert szám. Szokásos rendezéssel és az addíció‐tétel alkalmazásával minden tagban fellép

sin^{2} φ

sin φ

cos φ

és

cos^{2} φ

egyike:

\begin{matrix} sin^{2} φ cos (α + β) cos δ + sin φ cos φ [cos (α + β) sin δ + sin (α + β) cos δ] + \\ + cos^{2} φ sin (α + β) sin δ = k sin^{2} φ cos α + k sin φ cos φ sin α . \end{matrix}

A szögletes zárójelben

sin (δ + α + β) = sin (2 δ - γ)

áll, így

\begin{matrix} sin (α + β) sin δ cos^{2} φ + [sin (2 δ - γ) - k sin α] cos φ sin φ + \\ + [cos (α + β) cos δ - k cos α] sin^{2} φ = 0. \end{matrix}

Innen

sin^{2} φ

-vel osztva (

sin φ \neq 0

, mert

P

nincs az

A D

egyenesen)

ctg φ

-re másodfokú egyenletet kapunk:

\begin{matrix} {ctg}^{2} φ + m {ctg}^{2} φ + n = 0, \end{matrix}

ahol

\begin{matrix} m = \frac{sin (2 δ - γ) - k sin α}{sin (α + β) sin δ}, n = \frac{cos (α + β) cos δ - k cos α}{sin (α + β) sin δ} . \end{matrix}

Mármost a

P B C

háromszögből

\begin{matrix} \frac{x}{p} = \frac{sin β}{sin (φ + α + β)} . \end{matrix}

Ehhez (1) első egyenletét hozzávéve

p

kiküszöbölésével

\begin{matrix} x = \frac{a sin β sin φ}{sin α sin (φ + α + β)} . \end{matrix}

Numerikusan

k = 1, 603

b = 106, 9^{\circ}

2 δ - γ = 180, 9^{\circ}

m = - 0, 7730

n = - 1, 658

, így

ctg φ

két értéke

- 0, 958

és

1, 731

. Ezekből

φ = 133, 77^{\circ}

, ill.

30, 02^{\circ}

, az előbbivel azonban a

P B C

háromszög szögeinek összege nagyobb lenne

180^{\circ}

-nál, ez tehát nem megfelelő.

φ

utóbbi értékével pedig

x = B C = 109, 5

Székely Gábor (Budapest, Madách I. g. II. o. t.)

Megjegyzés: Kaphatunk (2)-ből

2 φ

szögfüggvényeire is egyenletet a törtek eltávolításával és a

2 sin u sin v = cos (u - v) - cos (u + v)

azonosság alkalmazásával:

\begin{matrix} a sin γ [cos α - cos (2 φ + α)] = c sin α [cos γ - cos (2 φ + 2 δ - γ)] . \end{matrix}

Innen az addíció‐tétel alkalmazásával

\begin{matrix} J cos 2 φ + K sin 2 φ = L \end{matrix}

alakú egyenletre jutunk. Láttuk az 1085. feladatban¹, hogy ennek megoldása:

\begin{matrix} cos 2 φ = \frac{J L \mp K \sqrt[]{J^{2} + K^{2} - L^{2}}}{J^{2} + K^{2}}, sin 2 φ = \frac{K L \pm J \sqrt[]{J^{2} + K^{2} - L^{2}}}{J^{2} + K^{2}} . \end{matrix}

A számítás kissé nehézkesebb a fentinél.

II. megoldás. Fejezzük ki

p

-t a

P A B

és

P B D

háromszögekből,

q

-t a

P C D

és

P A C

háromszögekből. A kifejezések egyenlőségéből:

\begin{matrix} (p =) & \frac{a sin φ}{sin α} = \frac{(x + c) sin (φ + δ)}{sin (β + γ)}, \\ (q =) & \frac{c sin (φ + δ)}{sin γ} = \frac{(x + a) sin φ}{sin (α + β)} . \end{matrix}

A két egyenlőség bal, ill. jobb oldalait összeszorozva a

φ

-t tartalmazó tényezők kiesnek. A megmaradt adatok közül csak

x

ismeretlen, ez tehát az

\begin{matrix} (x + a) (x + c) = \frac{a c sin (α + β) sin (β + γ)}{sin α sin γ} = M \end{matrix}

(3)

egyenletből kiszámítható:

\begin{matrix} x^{2} + (a + c) x - (M - a c) = 0, & (4) \\ x = B C = \frac{1}{2} [- (a + c) \pm \sqrt[]{{(a + c)}^{2} + 4 (M - a c)}] . \end{matrix}

Esetünkben

M > a c

, mert

\begin{matrix} 0^{\circ} < α < α + β < 90^{\circ}, és így \frac{sin (α + β)}{sin α} > 1, \\ 0^{\circ} < γ < γ + β < 90^{\circ}, és így \frac{sin (γ + β)}{sin γ} > 1, \end{matrix}

és 1-nél nagyobb számok szorzata nagyobb 1-nél. Így (4) állandó tagja, vagyis a gyökök szorzata negatív, tehát a gyökök valósak, és egyikük negatív, másikuk pozitív. Csak az utóbbit használhatjuk, kiszámítva

x = 109, 6

Lehel Jenő (Budapest, Apáczai Csere J. gyak. g. IV. o. t.)

Megjegyzések: 1. Hasonló egyenletre jutunk, ha kifejezzük a

P A B

P B C

P C D

és

P A D

háromszögek kétszeres területét egyrészt

P

-ből húzott közös

P P'

magasságukkal és az

A D

egyenesen levő alapjukkal, másrészt a

P

-ből kiinduló oldalaikkal és a közbezárt szögekkel, és a nyert egyenlőségek megfelelő oldalait összeszorozzuk. Így az

\begin{matrix} \frac{x (x + a + c)}{a c} = \frac{sin β sin (α + β + γ)}{sin α sin γ} \end{matrix}

(5)

egyenlet adódik.

Gálfi István (Budapest, Kandó K. hír. ip. t. III. o. t.)

2. (3) és (5) közvetlenül adódnak Papposz tételéből, amely szerint ha az egy

S

ponton átmenő

t

u

v

w

egyeneseket egy egyenes rendre a

T

U

V

W

pontokban metszi, akkor

\begin{matrix} \frac{T U}{U V} : \frac{T W}{W V} = \frac{sin T S U ∢}{sin U S V ∢} : \frac{sin T S W ∢}{sin W S V ∢} . \end{matrix}

Somogyi István (Ajka, Bródy I. g. II. o. t.)

¹K.M.L. 23 (1961/11) 131. o.