Feladat: 1253. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Berecz Ágota ,  Berky P. ,  Csirik J. ,  Csörnyei Z. ,  Dobozy Ottó ,  Érdi Bálint ,  Fodor Zsuzsa ,  Folly Gábor ,  Fülöp I. ,  Földeáki Mária ,  Földes Antónia ,  Gálfi István ,  Gazsó János ,  Gyárfás András ,  Hirka András ,  Hoffmann P. ,  Horváth J. ,  Jahn László ,  Karsai Kornélia ,  Kőszegi László ,  Kulcsár Gy. ,  Laufer Judit ,  Lehel Csaba ,  Lehel Jenő ,  Lénárt Zoltán ,  Lovász László ,  Makai Endre ,  Malatinszky G. ,  Márki László ,  Máté Zoltán ,  Minárik László ,  Nagy Klára ,  Simonovits András ,  Sófalvi M. ,  Somos Péter ,  Szajcz M. ,  Szalkai István ,  Székely Gábor ,  Szepesvári Gy. ,  Szidarovszky Ferenc ,  Szilágyi Tivadar ,  Szőcs A. ,  Sövényházi Mária ,  Tamás G. ,  Veres Ferenc 
Füzet: 1964/március, 104 - 106. oldal  PDF  |  MathML 
Témakör(ök): Negyedfokú (és arra visszavezethető) egyenletek, Trigonometrikus egyenletek, Szimmetrikus egyenletek, Numerikus és grafikus módszerek, Feladat, Síkgeometriai számítások trigonometriával
Hivatkozás(ok):Feladatok: 1963/május: 1253. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az ABC háromszögben CA=CB, az A-ból húzott magasság talppontja a BC egyenesen D, a C-ből húzott magasság talppontja1 E, legyen AE=1 és CE=x. Ekkor a közös hegyes szöggel bíró ABD és CBE derékszögű háromszögek hasonlóságából

AD=ABBC⋅CE=2x1+x2,
így a feltevés szerint
x+2x1+x2=1,
amiből nyilvánvalóan 0<x<1.
 
 
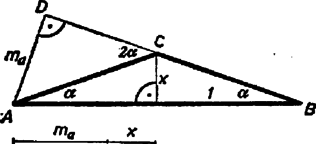1. ábra
 

Rendezésekkel és közben négyzetre emeléssel
2x=(1-x)1+x2,x4-2x3-2x2-2x+1=0.(1)


A bal oldal első és utolsó tagját tekintve kézenfekvőnek látszik megpróbálni a kifejezés kiegészítését egy x2+Ax±1 alakú polinom négyzetévé. Ez sikerül, mert az alap harmadik tagjának +1-et véve, A értéke gyanánt a bal oldali kifejezés második és negyedik tagjából egyaránt -1 adódik. Így
(x2-x+1)2=5x2,
és négyzetgyökvonással, majd újabb rendezéssel
x2-(1±5)x+1=0.(2)
5 előjelét negatívnak véve a diszkrimináns negatív: (6-25)-4<0, így nincs valós gyök. 5 előjelét pozitívnak véve a 0<x<1 követelménynek megfelelő gyök, négy tizedes jegyre pontosan
x=1+5-2+252≈0,3460.

Most már a háromszögnek az alapon levő szögeire tgBAC∢=x, így BAC∢=ABC∢≈19∘5', és ACB∢=140∘50'.
 
 Sövényházi Mária (Szeged, Ságvári E. gyak. g. III. o. t.)
 

Megjegyzés: Az (1) egy szimmetrikus egyenlet (szimmetrikusan elhelyezkedő együtthatói egyenlők), s így megoldható az azokra ismert általános eljárás szerint2: x2-tel való osztás (ugyanis x=0 nem lehet gyök) és x+1/x=y, x2+1/x2=y2-2 helyettesítéssel y2-2y-4=0, ami szintén a (2) egyenletre vezet.
 
 Kőszegi László (Baja, III. Béla g. IV. o. t.)
 

II. megoldás. CAB∢=α jelöléssel ACD∢=2α, így AD=ACsin2α, CE=ACsinα, AE=cosα, és a feltétel szerint, AC-tel mindjárt osztva
sinα+sin2α=cosα.
Átrendezés után négyzetre emelve, majd ismert azonosságok alkalmazásával
sin2α=cosα-sinα,sin22α=1-sin2α,(3)sin2α=-1+52≈0,6180,2α≈38∘10'.(4)


(A negatív gyököt figyelmen kívül hagytuk, mert α hegyes szög, 2α<180∘, tehát sin2α>0.)
 
 Karsai Kornélia (Szeged, Radnóti M. g. I. o. t.)
 

Megjegyzések. 1. A (3) egyenletet sin2α(sin2α+1)=1, másképpen sin2α: :1=1:(sin2α+1) alakban írva látjuk, hogy sin2α a sin2α+1 szakasznak az aranymetszés (folytonos arányosság szerint való osztás) útján keletkezett kisebb része. Ennek alapján az ABC háromszög alakja megszerkeszthető: az FG szakasz G végpontjában emelt merőlegesre felmérjük a GH=FG/2 szakaszt, H körül GH sugárral kört írunk, ezt az FH egyenes J-ben és K-ban metszi, FJ<FK. Messe az előbbi kört az J körül JF sugárral írt kör L-ben és az LK egyenes a K körül KJ sugárral írt kört M-ben, akkor a JKM háromszög hasonló a szóban forgó háromszöghöz. Állításunk bizonyítását az olvasóra bízzuk (2. ábra).
 
 
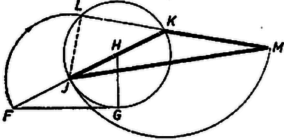2. ábra
 

 Simonovits András (Budapest, Radnóti M. gyak. g. II. o. t.)
 
2. Meghatározhatjuk α-t az
AD+CE=2sinα+tg α=1  (5)
egyenletből is. Ebben közelítő módszereket is használhatunk, mert a szögfüggvénytáblázat a szögre a kerekítések miatt általában csak közelítő értéket ad. tg α helyett a kisebb sinα-t írva 1=2sinα+tg α>3sinα, tehát sinα<1/3≈ ≈0,3333, α<19,47∘. Ha viszont sinα helyett a nagyobb tg α-t írjuk: 1<3tg α, tg α>0,3333, α>18,43∘. E két korlát még csak kb. foknyi pontossággal zárja körül α-t.
α=19,47∘ mellett 2sinα+tg α=0,6666+0,3535=1,0201, így olyan kisebb szöggel kell próbálkoznunk, amely mellett a bal oldal 0,0201-del kisebbnek adódik. A tg-függvény gyorsabban változik, mint a sin-függvény, ezért a csökkenésből legalább 0,0201:3=0,0067-et tg α csökkenése útján kell kapnunk:
tg α<0,3535-0,0067=0,3468, α<19,12∘,  
sinα csökkenéséből viszont legfeljebb 0,0067 adódhat: sinα>0,3333-0,0067=0,3266, α>19,06∘.
Innen máris 0,1∘-nál kisebb hibával α=19,1∘.
 
 Máté Zoltán (Bonyhád, Petőfi S. g. IV. o. t.)
 
3. Másképpen kapunk közelítő értéket a szögre abból az észrevételből, hogy az y=2sinx+tgx függvény grafikonját a 0≤x≤π/6 intervallumban 1/2%-nál kisebb hibával közelíti az y=3x függvény (x ívmértékben értendő). Ezért jó közelítő érték 3x=1-ből x=1/3=0,3333radián≈19,1∘. Próbát téve (5)-ben az α=19,0∘, 19,1∘ és 19,2∘ értékekkel a bal oldal értéke rendre 0,9955, 1,0007, ill. 1,0060, a középső áll legközelebb az előírt 1 értékhez, ezért 0,1∘ pontossággal α=19,1∘.
 
 Dobozy Ottó (Budapest, Apáczai Csere J. gyak. ált. isk. VII. o. t.)
1Az ábrán E pótlandó.

2Pl. 1176. feladatban látott módon, K. M. L. 26 (1963/1) 56. o.