Kezdőlap


Feladat:	1252. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antal Magdolna , Csirik J. , Földes Antónia , Hirka A. , Laufer Judit , Makai Endre , Nárai Gy. , Sófalvi M. , Somos P. , Székely G. , Szepesvári Gy. , Szidarovszky F. , Tamás E. , Veres F.
Füzet:	1965/január, 7 - 8. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Beírt háromszög, Pont körüli forgatás, Húrnégyszögek, Feladat
Hivatkozás(ok):	Feladatok: 1963/május: 1252. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1. ábra $A_{0} B_{0} C_{0}$ háromszögének szögei rendre a feladat adatainak megfelelő $a_{0} = 12^{\circ}$ , $β_{0} = 36^{\circ}$ , $γ_{0} = 132^{\circ}$ -os szögek, $A_{0} A_{1}$ , $B_{0} B_{1}$ , $C_{0} C_{1}$ a háromszög magasságvonalai, $A_{1} A_{2}$ , $B_{1} B_{2}$ , $C_{1} C_{2}$ pedig az $A_{1} B_{1} C_{1}$ talpponti háromszög magasságai, $A_{2} B_{2} C_{2}$ a szóban forgó második talpponti háromszög. Az ábráról úgy látszik, hogy az egymásnak megfelelő $A_{0} B_{0}$ és $B_{2} C_{2}$ , a $B_{0} C_{0}$ és $A_{2} B_{2}$ , továbbá a $C_{0} A_{0}$ és $A_{2} C_{2}$ oldalak szöge lehet $60^{\circ}$ -os, de az $A_{2} B_{2} C_{2}$ háromszög $A_{0} B_{0} C_{0}$ -hoz képest csak tompaszöggel, s így $120^{\circ}$ -kal lehet elforgatva az óramutató járásával megegyező irányban.

Bebizonyítjuk, hogy az utóbbi kapcsolat valóban fenn is áll. Ehhez kiszámítjuk az első és a második talpponti háromszög szögeit, továbbá azt, hogy ezek egyes oldalai mekkora szöggel vannak elfordulva az ábra egyes más oldal‐egyeneseihez képest.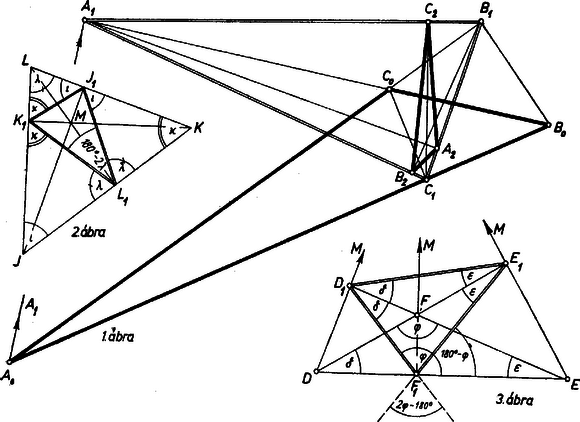

Az idézett feladatban közölt összefüggések felhasználásával az

A_{1} B_{1} C_{1}

háromszög egymás utáni csúcsainál levő szögek nagysága rendre:

\begin{matrix} a_{1} = 2 a_{0} = 24^{\circ}, β_{1} = 2 β_{0} = 72^{\circ}, γ_{1} = 2 γ_{0} - 180^{\circ} = 84^{\circ}, \end{matrix}

ugyanis az

A_{0} B_{0} C_{0}

háromszög tompaszögű. Ezek szerint

A_{1} B_{1} C_{1}

hegyesszögű háromszög, ennélfogva az

A_{2} B_{2} C_{2}

háromszög egymás utáni csúcsainál levő szög rendre:

\begin{matrix} a_{2} = 180^{\circ} - 2 a_{1} = 132^{\circ} = γ_{0}, β_{2} = 180^{\circ} - 2 β_{1} = 36^{\circ} = β_{0}, \\ γ_{2} = 180^{\circ} - 2 γ_{1} = 12^{\circ} = a_{0} . \end{matrix}

Eszerint a hasonlóságban az

A_{2}

B_{2}

C_{2}

csúcs rendre

C_{0}

-nak,

B_{0}

-nak, ill.

A_{0}

-nak felel meg, és a fent felsorolt oldalegyenes‐párok egymás megfelelői.
A háromszög oldalai és talpponti háromszögének egyes oldalai közti szögeket az eredeti háromszög szögeivel kifejezve a 3. ábrán egy tetszés szerinti tompaszögű háromszög esetében mutatjuk be, a 2. ábrán pedig egy hegyesszögű háromszög esetében. A beírt kifejezések bebizonyíthatók abból, hogy egy oldal két végpontjából húzott magasságok talppontjai az oldal, mint átmérő fölé írt Thalész‐körön vannak, és így pl. a 3. ábra

D

E

E_{1}

D_{1}

pontjai ebben a sorrendben, egy konvex húrnégyszög csúcsai.

A_{0} B_{0}

-t

A_{1} C_{1}

irányba forgatva az elforgatás szöge az óramutató járásával egyirányú és az

A_{1} C_{1} A_{0} ∢ = 180^{\circ} - γ_{0} = 48^{\circ}

váltószöge, tehát azzal egyenlő.

A_{1} C_{1} = A_{1} B_{2}

-t pedig

A_{1} B_{2} C_{2} ∢ = β_{1} = 72^{\circ}

váltószögével elforgatva jutunk

C_{2} B_{2}

irányú egyeneshez. A két elforgatás összege

120^{\circ}

, és ezt akartuk belátni.

Hasonlóan a

B_{0} C_{0}

, azaz

B_{0} A_{1}

irányból

C_{1} A_{1}

-be, vagyis

B_{2} A_{1}

-be, ebből pedig

B_{2} C_{2}

-n át

B_{2} A_{2}

-be vivő forgás nagysága

a_{0} + β_{1} + β_{2} = 120^{\circ}

.
E két forgásszög megegyezéséből, valamint az

A_{0} B_{0} C_{0}

és

C_{2} B_{2} A_{2}

háromszögek látott hasonlóságából már következik, hogy a két háromszög megegyező körüljárású, így a harmadik megfelelő oldalpár is, tehát a két háromszög a maga egészében is,

120^{\circ}

-os forgással vihető át egymásba. Ezzel meglátásunk helyességét igazoltuk. Eszerint a kérdéses állítás nem igaz, de helyessé válik, ha

60^{\circ}

helyett

120^{\circ}

-ot írunk.

Makai Endre (Budapest, Eötvös J. Gimn.)

Megjegyzések. 1. Elegendő egy megfelelő oldalpár elfordulási szögét meghatározni, ha előzetesen megállapítjuk, hogy a kérdéses háromszögek

A_{0} B_{0} C_{0}

, ill.

C_{2} B_{2} A_{2}

sorrendben való körüljárása megegyező irányú. Nem nehéz, de nem egészen rövid meggondolással belátható, hogy bejárva egy tompaszögű háromszög csúcsait valamilyen sorrendben, másrészt talpponti háromszögének rendre megfelelő csúcsait, ellentétes irányú körüljárásokat kapunk (3. ábra), másrészt hogy hegyesszögű háromszög és talpponti háromszöge azonos körüljárásúak (2. ábra).
2. A kérdés általában való vizsgálata esetén célszerű minden fellépő irányt azzal a szöggel meghatározni, amekkora forgás átvisz egy tetszés szerint választott kiindulási irányból az ugyancsak megválasztott forgási irány mentén az illető irányba. Elegendő tehát egy ún. polárkoordinátarendszerből¹ az alapirányt megválasztani. A pozitív (az óramutató járásával ellentétes) forgás irányában mért forgásszögeket célszerű használni, ha pozitív körüljárású háromszögből indulunk ki. Így esetünkben

+ 240^{\circ}

-os, vagyis abszolút értékben nagyobb forgási szög adódott volna.

3. Néhány dolgozat derékszögű koordinátarendszert választott alapul, és hosszabb számítás alapján adott helyes választ a kérdésre.

¹A polárkoordinátarendszerben a sík egy

P

pontjának helyzetét úgy határozzuk meg, hogy megadjuk egy előre megválasztott

O

ponttól ‐ az ún. pólustól ‐ való távolságát, ‐ az ún. rádiusz vektorát ‐, továbbá, annak a pozitív forgásnak a

φ

szögét (

0 \leq φ < 2 π

), amely egy előre megválasztott, az

O

-ból kiinduló félegyenesből ‐ az ún. polártengelyből, alapirányból az

O P

félegyenesbe átvisz.