Kezdőlap


Feladat:	1251. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Fodor Zsuzsa
Füzet:	1964/március, 102 - 104. oldal		PDF \| MathML
Témakör(ök):	Eltolás, Parabola egyenlete, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):	Feladatok: 1963/május: 1251. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Állítsuk a $g$ parabola síkját magunk elé függőleges helyzetben úgy, hogy a parabola $t$ tengelye függőleges legyen, és $C$ csúcsa lent legyen, vagyis a parabola az $i$ irányvonala fölött legyen. Jelöljük a parabola fókuszát $F$ -fel, paraméterét $p$ -ve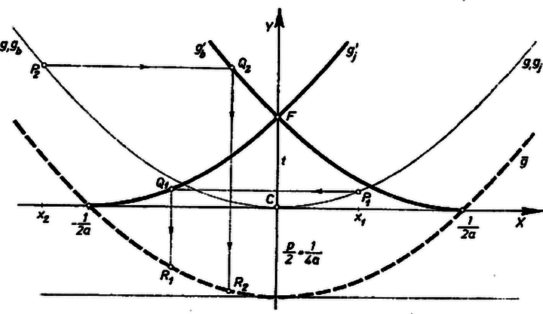l.

Mondhatjuk, hogy a

Q

pont a

P

pontból a tengely felé való eltolás útján keletkezik. Ha

P_{1}

a parabola jobb oldali ágán van, akkor az eltolás balra történik, a bal oldali ágon levő

P_{2}

esetében viszont jobbra. Arra az esetre, ha

P

a tengelyen van, vagyis azonos

C

-vel, a feladat nem határozta meg a felmérés, az eltolás irányát; mi azt vesszük, hogy akkor

C

akár jobbra, akár balra eltolható. Mivel az eltolás nagysága mindig

p

, nyilvánvaló, hogy

Q

mértani helye két parabolaág:

g

-nek

t

-től jobbra eső

g_{j}

ágát balra toljuk

p

-vel,

t

-től balra eső

g_{b}

ágát pedig jobbra toljuk

p

-vel.

Q

csak az így előálló

g'_{j}

-n vagy

g'_{b}

-n lehet, és e vonalak bármely

Z

pontjához van olyan

P

, amelyből éppen

Z

-be jutunk. (

Q

mértani helyének két ága

F

-ben metszi egymást, mert a parabola fókuszán átmenő és a tengelyre merőleges húrnak a hossza egyenlő a paraméter

2

-szeresével, végpontjai az eltolással

F

-be jutnak.)
A

Q

-ból

R

-be vivő eltolás nagysága

P

haladásával változik, ezt számítással követjük. Legyen

g

egyenlete

y = a x^{2}

, ahol

a > 0

, így a parabola szokásos

y^{2} = 2 p x

x = y^{2} / 2 p

egyenlet alakjával összehasonlítva

a = 1 / 2 p

, és a paraméter hossza

p = 1 / 2 a

. Legyen a

g_{j}

ág egy

P_{1}

pontjának abszcisszája

x_{1}

, azaz

x_{1} \geq 0

(megengedjük a

P_{1} = C

esetet is), tehát

P_{1}

-nek a tengelytől mért távolsága

x_{1}

, ordinátája pedig

y_{1} = a x_{1}^{2}

. Így a

P_{1}

-hől kiindulva keletkező

Q_{1}

koordinátái

(x_{1} - \frac{1}{2 a}, y_{1})

, tehát az ehhez tartozó

R_{1}

pont

(u, v)

koordinátáira

\begin{matrix} u = x_{1} - \frac{1}{2 a}, v = y_{1} - x_{1} . \end{matrix}

Kifejezve

P_{1}

koordinátáit

R_{1}

koordinátáival:

\begin{matrix} x_{1} = u + \frac{1}{2 a}, y_{1} = v + x_{1} = u + v + \frac{1}{2 a}, \end{matrix}

(1)

és ezeket beírva az

x_{1}

és

y_{1}

között fennálló összefüggésbe,

g

egyenletébe, megkapjuk

u

és

v

összefüggését, az

R_{1}

mértani helyét tartalmazó vonal egyenletét:

\begin{matrix} u + v + \frac{1}{2 a} = a (u^{2} + \frac{u}{a} + \frac{1}{4 a^{2}}) = a u^{2} + u + \frac{1}{4 a}, \\ v = a u^{2} - \frac{1}{4 a} . & (2) \end{matrix}

Itt

- 1 / 4 a = - p / 2 < 0

, eszerint

R_{1}

mindig rajta van azon a

\bar{g}

parabolán, amely

g

-ből úgy keletkezik, hogy azt eltoljuk a tengellyel párhuzamosan; az irányvonal felé a paraméter felével; más szóval

\bar{g}

fókusza a

C

pont, csúcsérintője az

i

egyenes.
Fordítva, ha

\bar{g}

-nak egy

R_{1}

(u, v)

pontjára

u \geq - 1 / 2 a

, akkor (1) szerint

x_{1} \geq 0

és

\begin{matrix} y_{1} = u + a u^{2} - \frac{1}{4 a} + \frac{1}{2 a} = a (u^{2} + \frac{u}{a} + \frac{1}{4 a^{2}}) = a {(u + \frac{1}{2 a})}^{2} = a x_{1}^{2}, \end{matrix}

tehát van

g_{j}

-nek olyan

P_{1}

pontja, amelyből az előírás szerint

R_{1}

-be jutunk,

R_{1}

hozzátartozik a mértani helyhez.

u < - 1 / 2 a

esetén viszont ilyen

P_{1}

pont nincs. Ezek szerint

\bar{g}

-nak az

u \leq - 1 / 2 a

egyenestől jobbra eső íve hozzátartozik a mértani helyhez.
Hasonlóan ha

P_{2}

g_{b}

ág egy pontja, azaz

x_{2} \leq 0

, akkor

P_{2}

-nek a tengelytől mért távolsága

| x_{2} | = - x_{2}

, ordinátája

y_{2} = a x_{2}^{2}

, és a fenti számítás így alakul:

\begin{matrix} Q_{2} (x_{2} + \frac{1}{2 a}, y_{2}), R_{2} (x_{2} + \frac{1}{2 a} = u, y_{2} - | x_{2} | = y_{2} + x_{2} = v), \\ x_{2} = u - \frac{1}{2 a}, y_{2} = v - u + \frac{1}{2 a}, \\ v - u + \frac{1}{2 a} = a (u^{2} - \frac{u}{a} + \frac{1}{4 a^{2}}), v = a u^{2} - \frac{1}{4 a} . \end{matrix}

Eszerint

R_{2}

\bar{g}

-on van, pontosabban

\bar{g}

-nak

u \leq 1 / 2 a

ívén, és a fentiekhez hasonlóan látható, hogy ez az ív is része

R

mértani helyének, és az előbbi ívvel együtt megadják a mértani hely összes pontjait, ugyanis a fenti két módon

g

minden pontjához megszerkesztettük

R

-et.
A két ív teljesen lefedi

\bar{g}

-t, és a

- 1 / 2 a \leq u \leq 1 / 2 a

ív pontjához

P

két helyzetéből is eljuthatunk. Ezek szerint

R

mértani helye az eredeti parabolából eltolással áll elő, a tengellyel párhuzamosan az irányvonal felé a paraméter felével.

Fodor Zsuzsa (Bp., Radnóti M. gyak. g. IV. o. t.)