Feladat: 1248. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Folly Gábor ,  Földes Antónia ,  Gálfi István ,  Gyárfás András ,  Komor Tamás ,  Kovács L. ,  Lovász László ,  Lukonics Gábor ,  Makai Endre ,  Pelikán József ,  Szép András ,  Szidarovszky Ferenc ,  Szilágyi Tivadar ,  Tamás Endre 
Füzet: 1964/május, 201 - 203. oldal  PDF  |  MathML 
Témakör(ök): Gömbi geometria, Mértani helyek, Feladat
Hivatkozás(ok):Feladatok: 1963/március: 1248. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az adott G gömb középpontja O, sugara R, az adott pont A, továbbá G-nek egy az A-ból derékszögben látható húrja (ha van ilyen) MM', és ennek felezőpontja 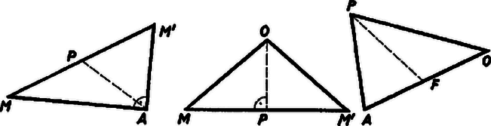P.

 
 
1. ábra
 

P egyszersmind az MM'A derékszögű háromszög körülírt körének középpontja, ezért PA=PM. Másrészt P ‐ ha különbözik O-tól ‐ az OMM' egyenlő szárú háromszög alapjának felezőpontja, ezért PO2+PM2=OM2, és az előbbi egyenlőség figyelembevételével
PO2+PA2=R2(1)
(Ez akkor is érvényes, ha P és O egybeesnek, mert ekkor PA=OA=OM=R, A a G gömbön van. Fordítva, ha A a G felületén van, akkor nyilvánvaló, hogy G-nek csak az átmérői láthatók A-ból derékszögben, ezért a keresett mértani hely egyetlen pontból áll: O-ból. Ezt a helyzetet tovább figyelmen kívül hagyjuk.)
(1)-ből következik, hogy P-nek az AO szakasz F felezőpontjától mért távolsága állandó, ugyanis PF az OAP háromszögben az OA oldalhoz tartozó súlyvonal, ezért ismert összefüggés szerint
PF2=14[2(PO2+PA2)-OA2]=14(2R2-OA2),(2)
ami állításunkat igazolja. Egyszersmind azt is látjuk, hogy a feltételnek megfelelő P pont (s így egyben A-ból derékszögben látszó húr is) csak akkor van, ha ez a kifejezés nem negatív, tehát ha OA2≤2R2. Ezt a továbbiakban feltesszük. Ha itt a ,,<'' jel érvényes, akkor P rajta van egy az F pont körül írt g gömb felületén, amelynek sugara
r=122R2-OA2=R22-OF2,(3)
tehát a keresett mértani hely része ennek a gömbfelületnek. Az OA2=2R2 esetre később visszatérünk.
Bebizonyítjuk, hogy g felületének minden pontja hozzátartozik a mértani helyhez. A mértani hely pontjai nyilván csak G belső pontjai lehetnek, ezért először azt látjuk be, hogy g minden pontja G belsejében van. (3) szerint OF<R/2, tehát F benne van az O körül R/2-sugárral írt G' gömb belsejében, így G-ben is. G-nek F-hez legközelebbi pontja az OF félegyenesen levő gömbsugár B végpontja. Így azt kell megmutatnunk, hogy 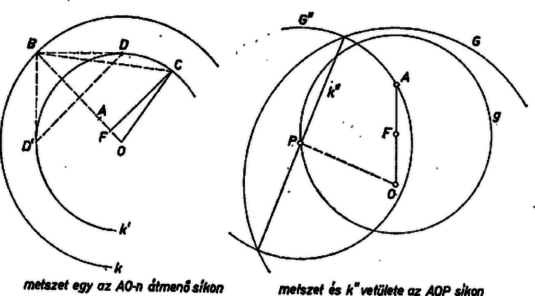r≤BF.
 
 
2. ábra
 

Messe egy az OA egyenesen átmenő sík G-t és G'-t a k, ill. k' körben. Húzzuk meg k'-nek az F-en átmenő, OF-re merőleges húrját, legyen ennek egyik végpontja C. Így r-et megadja CF; az r=CF≤BF állítás pedig egyértelmű azzal, hogy a BCF derékszögű háromszög C-nél levő hegyesszöge nagyobb, vagy ugyanakkora, mint a B-nél levő hegyesszöge, más szóval, hogy a B-nél levő szög kisebb, mint 45∘, vagy egyenlő vele.
A k'-höz B-ből húzott érintők érintési pontját D-vel és D'-vel jelölve a k' bármely pontjához B-ből húzott félegyenes a DBD' szögtartomány belsejében halad vagy annak határán, tehát CBF∢≤DBF∢. A BOD derékszögű háromszögből viszont BD2=BO2-DO2=R2/2=DO2, ez a háromszög egyenlő szárú, és így DBO∢=DBF∢=45∘. Eszerint állításunk helyes, g-nek nincs pontja G-n kívül. Maga B sem lehet rajta g felületén, mert BF=r=CF csak akkor teljesül, ha C azonos D-vel vagy D'-vel, ekkor azonban F felezi OB-t, tehát A azonos B-vel, ezt az esetet viszont kizártuk.
Megmutatjuk most már, hogy g-nek tetszés szerinti P pontjához megadható G-nek olyan MM' húrja, amely A-ból derékszögben látszik, és amelynek felezőpontja P. Írjunk P körül PA sugárral G'' gömböt. G és G'' egy k'' körben metszik egymást, amely nem fajul ponttá, ugyanis a két gömbsugár különbsége kisebb középpontjaik távolságánál:
R-PA<PO,azazPO+PA>R,
mert az utóbbi egyenlőtlenségben mindkét oldal pozitív, tehát az egyenlőtlenség akkor és csak akkor teljesül, amikor (PO+PA)2>R2, ez pedig (1) miatt teljesül. (Ugyanis P különbözik O-tól is, A-tól is, mert az r=OF=AF feltevés a kizárt OA=R-re vezet.)
k''-nek bármely MM' átmérője megfelel állításunknak: A-ból derékszögben látszik, és felezőpontja P. Az utóbbi feltétel teljesül, mert k'' középpontja P, vagyis k'' a G''-nek főköre. Valóban, k'' minden M pontjára MP=PA és MO=R, ezért (2) és (3) alapján
MP2=PA2=2FP2-OP2+OA22=R2-OP2=MO2-OP2,
tehát az MPO szög derékszög, k'' a P-n átmenő és OP-re merőlegesen álló síkban van. Így viszont az első feltétel is teljesül, mert k'' átmérői egyben G''-nek is átmérői, és így a G'' felületén levő A-ból Thalész tétele szerint derékszögben láthatók. (Maga A nincs rajta k''-n, mert k'' a G-n van, A pedig nincs rajta.) Ezek szerint a keresett mértani helyet OA2<2R2 esetén a g felületén levő pontok alkotják.
Az OA2=2R2 esetre nyilvánvaló, hogy annak a kúpnak, melynek alkotói az A-ból G-hez húzható összes érintők, a félnyílásszöge 45∘, és így A-ból csak olyan húrok láthatók derékszögben, melyek mindkét végpontja a kúp és G érintkezési körén van, és az ilyenek is csak akkor, ha a mondott körnek átmérői. Ekkor viszont P a mondott kör középpontja. Könnyű belátni, hogy e középpont egyben az OA szakasz felezőpontja.
 
 Lukonics Gábor (Aszód, Petőfi S. Gimn., IV. o. t.)