Kezdőlap


Feladat:	1246. matematika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berecz Ágota , Folly Gábor , Földes Antónia , Gyárfás A. , Horváth J. , Kiss Katalin , Lovász László , Makai Endre , Malatinszky G. , Marosi Judit , Nagy Klára , Rejtő Lídia , Szidarovszky Ferenc , Tamás G.
Füzet:	1964/november, 117 - 119. oldal		PDF \| MathML
Témakör(ök):	Alakzatok egybevágósága, Negyedfokú (és arra visszavezethető) egyenletek, Fizikai jellegű feladatok, Trigonometria, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1963/március: 1246. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás.^{$^{*}$} 1. Az állítást tömegpontrendszerek súlypontjára vonatkozó meggondolásokkal bizonyítjuk. Az $m_{1}$ tömegű $P_{1}$ pont és $m_{2}$ tömegű $P_{2}$ pont súlypontján azt az $m_{1} + m_{2}$ tömegű $S$ pontot értjük a $P_{1} P_{2}$ szakaszon, amelyre $P_{1} S / S P_{2} = m_{2} / m_{1}$ . Több tömegpontból álló rendszer súlypontjához úgy juthatunk, hogy vesszük két tömegpont súlypontját, majd sorra már tekintetbe vett pontok súlypontjának és egy további tömegpontnak a súlypontját, míg minden pont sorra nem kerül. Az egyes pontokban elhelyezett tömegekre ható (párhuzamosnak feltételezett) nehézségi erők eredője a súlypontban ható és az ahhoz rendelt tömegnek megfelelő nehézségi erővel egyenlő. Világos, hogy egy síkban levő pontrendszer súlypontja ebben a síkban van.

Fel fogjuk használni, hogy egy tömegpontrendszer súlypontja független a pontok sorrendjétől, és hogy részekre osztva a pontrendszert, az egyes részrendszerek súlypontjainak súlypontja az egész rendszer súlypontja.
Ha egy szabályos

n

-szög minden csúcsába egységnyi tömeget helyezünk, akkor a rendszer súlypontja a sokszög középpontja (a körülírt kör középpontja)

n

egységnyi tömeggel. Valóban, ha a sokszöget a középpont körül a teljes körülfordulás

n

-ed részével forgatjuk el, akkor önmagába megy át, tehát súlypontja változatlan marad. Forgatásnál azonban egyedül a forgatás középpontja nem mozdul el, tehát itt van a súlypont.
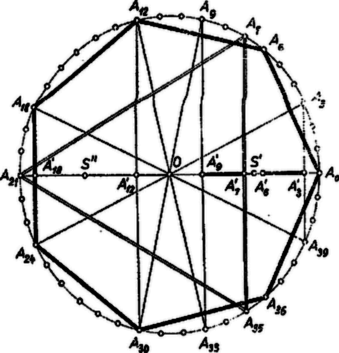
Esetünkben az

A_{0}

A_{6}

A_{7}

A_{12}

A_{18}

A_{21}

A_{24}

A_{30}

A_{35}

A_{36}

egységnyi tömegű pontokból álló

R

rendszer súlypontja is a kör

O

középpontja, mert felbontva az

A_{7}

A_{21}

A_{35}

pontok szabályos háromszöget alkotnak (két-két pont közt a kör

14

negyvenketted része van), a maradó pontok pedig szabályos hétszöget (két-két pont közt a kör

6

negyvenketted része van). Így mindegyik részrendszer súlypontja

O

, tehát az

R

rendszeré is.
Ugyancsak

O

a súlypontja a körön átellenes

A_{0}

és

A_{21}

pontokba helyezett tömegek alkotta

R_{1}

rendszernek is. Így a többi

8

tömegpont

R_{2}

rendszerének súlypontja ugyancsak

O

, mert különben az

R_{1}

és

R_{2}

egyesítésével újra adódó

R

súlypontja nem lehetne

O

.
Bontsuk fel

R_{2}

-t két rendszerre, 4‐4 tömegponttal, az egyik

A_{6}

A_{7}

A_{35}

A_{36}

, a másik

A_{12}

A_{18}

A_{24}

A_{30}

. E részrendszerek

S'

, ill.

S''

súlypontja az

O

-ra tükrös pontpár, mert az újraegyesítéssel visszanyert

R_{2}

súlypontja csak így lesz

O

S'

A_{0} A_{21}

átmérőn van, mert az

A_{6}

A_{36}

és

A_{7}

A_{35}

pontpárok a kiindulási pontrendszerben erre az átmérőre tükrösek, így az első pontpár súlypontja az egybeeső

A_{6}' \equiv A_{36}'

pont, az utóbbié ugyanígy

A_{7}'

, egyaránt 2‐2 egységnyi tömeggel, ennélfogva

S'

azonos az

A'_{3} A'_{7}

szakasz felezőpontjával. Hasonlóan

S''

A'_{12} A'_{18}

szakasz felezőpontja.
Ábránkat

O

-ra tükrözve

A_{12}

A_{18}

A_{24}

A_{30}

rendre az

A_{33}

A_{39}

A_{3}

A_{9}

pontba megy át,

S''

pedig ezek szerint az

A'_{3} A'_{9}

szakasz felezőpontjába, másrészt fenti megállapításunk szerint

S'

-be. Azt kaptuk tehát, hogy az

A_{0} A_{21}

egyenes

A'_{6} A'_{7}

és

A'_{2} A'_{9}

szakaszainak felezőpontja közös. Így pedig az

A'_{3} A'_{6}

és

A'_{7} A'_{9}

szakaszok egymás tükörképei a mondott felezőpontra nézve, tehát egyenlők.

II. megoldás. Legyen a kör sugara egységnyi. A rövidebb

A_{0} A_{3}

A_{0} A_{6}

A_{0} A_{7}

A_{0} A_{9}

ívhez tartozó középponti szög (ívmértékben mérve)

π

-nek rendre:

3 / 21 = 1 / 7

része, ill.

2 / 7

1 / 3

3 / 7

része. Ezért a szóban forgó vetületi pontoknak a kör

O

középpontjától mért távolságai rendre

\begin{matrix} O A'_{3} = cos \frac{π}{7}, O A'_{6} = cos \frac{2 π}{7}, O A'_{7} = cos \frac{π}{3} = \frac{1}{2}, O A'_{9} = cos \frac{3 π}{7}, \end{matrix}

mindegyik pozitív és csökkenő sorozatot alkotnak. Ezekkel a vizsgálandó szakaszpár különbsége

\begin{matrix} d = A'_{9} A'_{7} - A'_{6} A'_{3} = \frac{1}{2} - cos \frac{3 π}{7} - cos \frac{π}{7} + cos \frac{2 π}{7}, \end{matrix}

(1)

erről kell megmutatnunk, hogy

0

-val egyenlő.
Jelöljük

π / 7

-et

δ

-val és fejezzük ki a

d

-t

y = cos δ

-val. Felhasználva a következő azonosságokat:

\begin{matrix} cos 2 α & = 2 cos^{2} α - 1, \\ cos 3 α & = cos (2 α + α) = cos 2 α cos α - sin 2 α sin α = 2 cos^{3} α - cos α - \\ - 2 sin^{2} α cos α = 4 cos^{3} α - 3 cos α, \end{matrix}

adódik

\begin{matrix} d = - 4 y^{3} + 2 y^{2} + 2 y - \frac{1}{2} . \end{matrix}

(2)

Másrészt

3 δ

kiegészítő szöge

4 δ

, tehát fennáll:

\begin{matrix} cos 3 δ + cos 4 δ = 0. \end{matrix}

(3)

Innen a fentiek és a

\begin{matrix} cos 4 α = 2 cos^{2} 2 α - 1 = 8 cos^{4} α - 8 cos^{2} α + 1 \end{matrix}

azonosság alapján

\begin{matrix} 8 y^{4} + 4 y^{3} - 8 y^{2} - 3 y + 1 = 0. \end{matrix}

(4)

Ez az egyenlet négy

y

értékre teljesülhet, minden olyan

cos z = y

-ra, amely mellett teljesül a (3)-nak megfelelő

cos 3 z + cos 4 z = 0

, vagyis

3 z + 4 z = 7 z = (2 k + 1) π

, ahol

k

egész szám. Mindjárt ilyen

z = π

, ekkor

y = - 1

, ez tehát (4) egyik gyöke, a bal oldalból kiemelhető az

y + 1

gyöktényező. A hányados

8 y^{3} - 4 y^{2} - 4 y + 1

, tehát a további gyökökre

\begin{matrix} 8 y^{3} - 4 y^{2} - 4 y + 1 = 0. \end{matrix}

(5)

Ez fennáll

cos δ

-ra is (mert

cos δ

nem azonos a leválasztott gyökkel, hiszen

δ < π / 2

, és ezért

cos δ = y > 0

).
Vegyük észre, hogy (5) bal oldalán (2)-nek

- 2

-szerese áll. Eszerint

- 2 d = 0

, és így

d = 0

. Ezt akartuk bizonyítani.

Pelikán József (Budapest, Fazekas M. gyak. g.)

Megjegyzés. A fenti meggondolást folytatva (5) teljesül minden

\begin{matrix} z = (2 k + 1) \frac{π}{7} = (2 k + 1) δ \end{matrix}

értékre, és ha

2 k + 1

nem osztható

7

-tel, mindezekkel

d = 0

. Ebből további, a feladatban kimondotthoz hasonló egyenlőségek fennállására következtethetünk, ezek azonban lényegesen új összefüggést nem adnak, a feladatban szereplő szakaszokból egyszerű transzformációkkal kaphatók.

^{$^{*}$}Ezt a megoldást Kárteszi Ferenc bocsátotta rendelkezésünkre.