Feladat: 1245. matematika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bak Zsuzsanna ,  Berecz Ágota ,  Csirik J. ,  Deák István ,  Dobó Ferenc ,  Folly Gábor ,  Földes Antónia ,  Hirka A. ,  Horváth J. ,  Jahn László ,  Kuzmann Ernő ,  Lovász László ,  Makai Endre ,  Malatinszky G. ,  Marosi Judit ,  Nagy Klára ,  Nárai György ,  Pelikán József ,  Rejtő Lídia ,  Szidarovszky Ferenc ,  Szilágyi Tivadar ,  Tamás Endre ,  Tamás G. ,  Treer Mária 
Füzet: 1964/február, 60 - 64. oldal  PDF  |  MathML 
Témakör(ök): Szögfelező egyenes, Egyenesek egyenlete, Paralelogrammák, Párhuzamos szelők tétele, Síkgeometriai számítások trigonometria nélkül, Feladat
Hivatkozás(ok):Feladatok: 1963/március: 1245. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. α) Jelöljük az A, B, C, D ponton át az előírás szerint meghúzott egyenest rendre a, b, c, d-vel, az a, d egyenespár metszéspontját M-mel, a b, c egyenespárét N-nel. Ekkor az MN álló megy át e-nek és f-nek O metszéspontján és felezi a köztük levő 2 pár csúcsszög egyikét.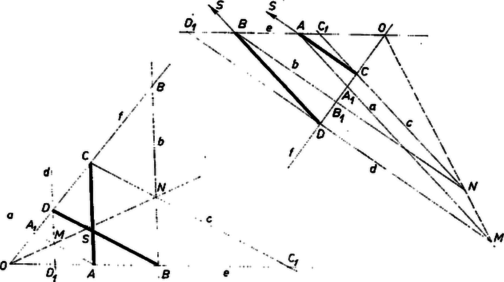
Állítjuk, hogy M is, N is egyenlő távolságra van e, f mindegyikétől. Ehhez megmutatjuk, hogy a MAB és MCD háromszögek területe egyenlő, és ugyanígy az NAB, NCD háromszögpáré is. Ebből következik, hogy az M-ből, ill. N-ből húzott magasságaik egyenlők, mert az e-n fekvő AB és az f-en fekvő CD alapjaik egyenlők.

 
 
1. ábra   és  2. ábra
 

Az AC és BD egyenesek metszéspontját S-sel jelölve a szerkesztés folytán az AMDS és a CNBS négyszög paralelogramma. Ekkor, az idomok területét ugyanúgy jelölve, mint magukat az idomokat, a szerkesztés folytán valóban
MAB=MAS=MSD=MCDés(1)NAB=NSB=NCS=NCD.(2)
Így M is, N is az e, f egyenespár valamelyik szögfelezőjén van.
 

β) Azt kell még belátnunk, hogy M és N az egyenespár ugyanazon szögfelezőjének pontja, vagyis az egyenespárral meghatározott 4 szögtartomány közül vagy ugyanabban vannak, vagy pedig két csúcsszögtartományban. Ha az adott pontok O-nak ugyanazon oldalán vannak és a sorrend e-n: O, A, B, f-en pedig O, D, C (1. ábra), akkor a és b-nek f-fel való metszéspontját A1-gyel, ill. B1-gyel,1 c és d-nek e-vel való metszéspontját C1-gyel, ill. D1-gyel jelölve a pontok sorrendje e-n D1, A, B, C1, f-en pedig A1, D, C, B1. Nyilvánvaló ugyanis, hogy a metszéspontok O-nak ugyanazon oldalán vannak, mint az adott pontok, továbbá hasonló háromszögekből OD1=OA⋅OD/OC<OA, OC1=OB⋅OC/OD>OB, és ugyanígy OA1<OD, és OB1>OC. Ennélfogva ADA1D1 és BCB1C1 konvex négyszögek, és benne vannak a 180∘-nál kisebb AOC szögtartományban, tehát ez áll átlóiknak M, ill. N metszéspontjára is.
C és D sorrendjét az előbbihez képest megfordítva feltehetjük, hogy OA>OC (ugyanis OA=OC esetén BD∥AC, a paralelogramma elfajul, az átló határozatlan). Ekkor A1 és B1 a CD szakaszon vannak (2. ábra), mert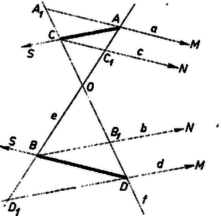
CB1=OCOA⋅AB<AB=CDésDA1=ODOB⋅BA<BA=DC,
ugyanis OD=OC+CD<OA+AB=OB. Ezért A1 közelebb van d-hez, mint C (azaz mint A), tehát A-ból A1 felé haladva közeledünk d-hez, ezért a és d-nek M metszéspontja A1-en túl adódik, abban a szögtartományban, amely az AOC szögtartománnyal az OC félegyenes mentén határos. Ugyanez áll N-re is, mert B1 közelebb van c-hez, mint D és B.
 
 
3. ábra
 

Hasonló maggondolás mutatja, hogy M és N akkor is az e és f közti 4 szögtartomány közül ugyanabban vannak, ha O az AB és CD szakaszok mindegyikének pontja (3. ábra). Ha viszont O az AB és CD szakaszok egyikén rajta van, másikán nem, akkor M és N két csúcsszögtartományban van (4. ábra), tehát ekkor is ugyanazon szögfelező egyenes pontjai.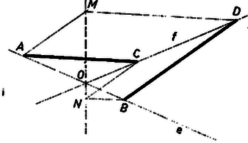
 
 
4. ábra
 

Ha A, B, C és D közül egy vagy kettő az O-ban van, akkor M és N egyike azonos O-val, ezért az utóbbi vizsgálat felesleges, vagy a paralelogramma határozatlan, az állításnak nincs értelme.
 
 Kuzmann Ernő (Budapest, I. István g. IV. o. t.)
 dolgozatából, kiegészítve a β) résszel. 
 
Megjegyzés. A β) rész 4 esetét egyszerre intézhetjük el, ha (1)-ben és (2)-ben a háromszögek körüljárási irányát is tekintetbe vesszük. A felhasznált háromszögek felírt körüljárása (1)-ben is, (2)-ben is egyező, mert az első és a harmadik lépésben az elhagyott és az új csúcs összekötő egyenese párhuzamos a megmaradó oldallal ‐ pl. BS∥MA ‐, a második lépésekben pedig az AMDS, ill. CNBS paralelogramma MS, ill. NS átlóján másodszor az elsővel ellentétes irányban haladtunk végig.
Ha mármost M és N az e egyenes ugyanazon oldalán vannak, akkor az MAB és NAB háromszögek körüljárása megegyező. Ezért egyezik egymással MCD és NCD körüljárása is, tehát M és N az f-nek is ugyanazon oldalán vannak, vagyis az e és f közti 4 szögtartomány közül ugyanabban. Ha pedig e szétválasztja az M, N pontpárt, akkor az MAB és NAB körüljárások iránya ellentétes, ugyanez áll az MCD és NCD körüljárásra is, tehát M-ből N-be haladva e és f mindegyikét átlépjük, M és N két csúcsszögtartományban van.
 
II. megoldás. Az 1. ábrán az OC1C szög szárait átmetszik a BN=b és AC párhuzamos egyenesek, ezért C1N:NC=C1B:BA; másrészt a C1OC szög szárait a C1C, BD és AA1 párhuzamosok, ezért C1B:BA=CD:DA1=BA:DA1=AO:A1O=C1O:CO, tehát C1N:NC=C1O:CO. Eszerint a C1OC háromszögben a C1OC szög felezője a C1C oldalt N-ben metszi. Hasonlóan adódik, hogy OM is felezi az e és f közti szöget.
Minthogy azonban a háromszög szögfelezőjének osztásarányára vonatkozó, itt felhasznált tétel a külső szög felezőjére is érvényes ‐ hacsak a háromszög nem egyenlő szárú ‐, azért itt is bizonyítani kell, hogy M és N ugyanazon szögfelező pontjai.
 
 Földes Antónia (Budapest, Apáczai Csere J. gyak. g. III. o. t.)
 dolgozata, kiegészítéssel.    
 
Nincs szükség annak külön bizonyítására, hogy az MN átló átmegy O-n, ha a koordinátageometria módszereivel bizonyítjuk az állítást:
 
III. megoldás. Válasszuk az e és f egyenesek O metszéspontját a derékszögű koordinátarendszer origójának, és legyenek a rendszer tengelyei e és f szögfelezői. Így az AB és CD szakaszoknak a tengelyeken levő vetületei egyenlő hosszúak. Az abszcissza tengelyen való vetületüket p-vel és e iránytényezőjét m-mel jelölve az ordinátatengelyen levő vetületük mp, az X tengelyt úgy választva ki és úgy irányítva, hogy p, m pozitívok legyenek (m=0 mellett f egybeesnék e-vel, p=0 mellett szintén). Legyen A és C abszcisszája x1, ill. x2, így B abszcisszája x1+p, D-é pedig x2+p, vagy x2-p aszerint, hogy D abszcisszája nagyobb mint C-é, vagy kisebb. Így az összes koordináták:
A(x1,mx1),B[x1+p,m(x1+p)],C(x2,-mx2),D[x2±p,-m(x2±p)].
(p kétféle előjeli lehetőségét később fogjuk szétválasztani.) Ezekből a szükséges irányok iránytényezői:
AC:m(x1+x2)x1-x2=m',BD:m(x1+x2+p±p)x1-x2+p±p=m''.
Felírjuk az ezekkel B-n és D-n át, ill. A-n és C-n át húzott b, d, a, ill. c párhuzamos egyenes egyenletét, majd abból a két tengellyel való metszéspontjuk abszcisszáját, ill. ordinátáját:
 


b:y-m(x1+p)=m'(x-x1-p),d:y+m(x2±p)=m'(x-x2∓p),a:y-mx1=m''(x-x1),c:y+mx2=m''(x-x2)
 


X-et metszik rendre  Y-t metszik rendreaz alábbi abszcisszán:az alábbi ordinátán:b1=2x2(x1+p)x1+x2,b2=-m'b1=-2mx2(x1+p)x1-x2;cd1=2x1(x2±p)x1+x2,d2=-m'd1=-2mx1(x2±p)x1-x2;a1=2x1(x2±p)x1+x2+p±p,a2=-m''a1=-2mx1(x2±p)x1-x2+p∓p;cc1=2x2(x1+p)x1+x2+p±p,c2=-m''c1=-2mx2(x1+p)x1-x2+p∓p;
 


Ezek szerint, ha p előtt a felső előjel érvényes, akkor b2=c2, és d2=a2, vagyis mind a b, c, mind a d, a egyenespár az Y-tengelyen metszi egymást, ha pedig az alsó előjel érvényes, akkor b1=c1 és d1=a1, vagyis egyenespárjaink metszéspontjai az X-tengelyen vannak.
A +p esetére vonatkozó állításunk nem érvényes, ha x1, x2, mert így b2, d2, a2 és c2, nevezője 0. Ez esetben az állításnak sincs értelme, mert AC∥BD∥Y, a kérdéses paralelogramma nem jön létre. Hasonló elfajulás adódik, ha -p esetében 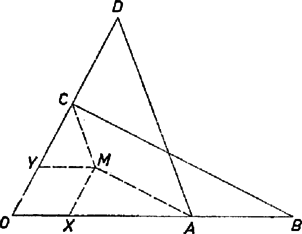x1=-x2, ekkor AC∥BD∥X.
 
 Makai Endre (Budapest, Eötvös J. g. II. o. t.)
 
 
5. ábra
 

IV. megoldás. Megmutatjuk, hogy az A-n át BC-vel és C-n át AD-vel húzott párhuzamosok M metszéspontja az egyik szögfelezőn van. Az OA és OC szögszárakkal párhuzamos szakaszoknak tulajdonítsunk pozitív vagy negatív előjelet, amint a szakasz OA-val, ill. OC-vel egyirányú vagy ellentétes irányú. Az M ponton át OC-vel párhuzamos egyenes messe az OA egyenest az X pontban, az OA-val párhuzamosan húzott egyenes OC-t Y-ban. Ekkor az OBC és XAM, továbbá az ODA és YCM háromszögek megfelelő oldalai párhuzamosak, így a háromszögek hasonlók és körüljárásuk is megegyező, tehát a betűzés sorrendjében a megfelelő oldalpárok vagy mind egyező, vagy mind ellentétes irányúak. Ezért a szögszárakkal párhuzamos oldalak arányát felírva, az előjeles távolságokra fennáll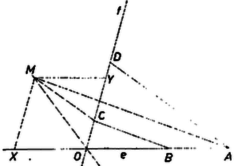
OBXA=OCXM=OCOYésODYC=OAYM=OAOX;
felhasználtuk, hogy az OXMY paralelogrammában XM és OY, továbbá YM és OX egy irányban párhuzamosak. A törteket eltávolítjuk, az XA és YC távolságokat OA-OX, ill. OC-OY alakba írjuk:
OB⋅OY=(OA-OX)⋅OC,OD⋅OX=(OC-OY)⋅OA,
vagy átrendezve
OC⋅OX+OB⋅OY=OA⋅OC,OD⋅OX+OA⋅OY=OA⋅OC.
Vonjuk ]e a második egyenlőséget az elsőből:
(OC-OD)⋅OX+(OB-OA)⋅OY=0,vagyDC⋅OX+AB⋅OY=0.
Itt CD és AB egyenlő hosszúak. Ha az előbbi OC-vel, az utóbbi OA-val egyirányú, vagy mindkettő ellentétes irányú, akkor a nyert egyenletből OX=OY következik, ha pedig az egyik szakaszpár egyirányú, a másik ellentétes irányú, akkor OX=-OY.
 
 
6. ábra
 

Azt nyertük tehát, hogy az OXMY paralelogramma rombusz, s így OM az XOY szög szögfelezője. Ez a szög az AOC szög, vagy a csúcsszöge, ha az OA és AB, valamint OC és CD egyirányúak, vagy mindkét pár ellentétes irányú. Ha viszont a két pár egyike egyirányú, a másika ellentétes irányú, akkor az M pont az AOC szöget 180∘-ra kiegészítő csúcsszögpár szögfelezőjén van. Ebből az is következik, hogy ha A és B, továbbá C és D szerepét egyidejűleg felcseréljük, akkor ismét ugyanazon a szögfelezőn levő pontot kapunk; másrészt az így nyert N pont a feladatban leírt paralelogramma M-mel átellenes csúcsa. Az MN átló tehát valóban az e, f egyenesek egyik szögfelezőjén van.
 
Megjegyzés: A fenti megoldás azt is adja, hogy ha AB és CD nem egyenlők, az MN egyenes akkor is átmegy O-n. Valóban, akkor is fennáll OX/OY=AB/CD, tehát az OXMY paralelogramma alakja csak az AB, CD (irányított) szakaszok arányától függ. A és B, továbbá C és D egyidejű felcserélésével tehát egy az előbbihez hasonló OX'NY' paralelogrammához jutunk, amiből következik az állítás, ami egyébként az I. megoldásból is könnyen kiolvasható.
1Az ábrán B1 indexe pótlandó.