Feladat: 1242. matematika feladat Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Csirik József ,  Deák István ,  Folly Gábor ,  Gyárfás András ,  Lovász László ,  Makai Endre ,  Nárai György ,  Pelikán József ,  Somos Péter ,  Szidarovszky Ferenc ,  Szilágyi Tivadar ,  Tamás Endre 
Füzet: 1964/február, 56 - 59. oldal  PDF  |  MathML 
Témakör(ök): Másodfokú diofantikus egyenletek, Ellipszis egyenlete, Feladat
Hivatkozás(ok):Feladatok: 1963/március: 1242. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egyenlet bal oldala az x, y ismeretlenekre szimmetrikus. Ha tehát

x1=a,y1=b
egy megfelelő megoldása az egyenletnek, vagyis egyrészt
a2-ab+b2=n,(1)
másrészt a, b pozitív egész számok ‐ akkor megoldás az
x2=b,y2=a
számpár is, és ez az előbbitől különböző, ha
a≠b.(2)

Továbbá a bal oldal mindegyik tagja másodfokú. Ezért az előbbi számok helyére negatívjukat téve ismét megoldást kapunk:
x3=-a,y3=-b;x4=-b,y4=-a,
és ezek az előbbiektől különbözők, valamint (2) miatt egymástól is, más szóval akkor, ha x1≠y1.
Az a2-ab+b2=(a2+b2)-ab kifejezés az alábbiak szerint két más módon is írható olyan különbség gyanánt, melyben a kisebbítendő két szám négyzetösszege, a kivonandó pedig ugyanezen két szám szorzata:
{=(a-b)2a2-ab+b2=(a-b)2+ab==(a-b)2-a2+ab+a2=(a-b)2-(a-b)a+a2,=(a-b)2+ab-b2+b2=(a-b)2-(a-b)(-b)+(-b)2.(3)
Ezeket (1)-gyel egybevetve egyenletünknek az alábbi x5, y5 és x9, y9 számpárok is megoldásai, továbbá az a 3‐3 további számpár is, amelyet belőlük a fenti mintára, felcseréléssel, ill. az előjelek egyidejű megváltoztatásával kapunk:
x50=a-b,y50=a;x60=y5=a,y60=x5=a-b;x70=-x5=-a+b,y70=-y5=-a;x80=-y5=-a,y80=-x5=-a+b;x90=a-b;y90=-b;x10=y9=-b,y10=x9=a-b;x11=-x9=-a+b,y11=-y9=b;x12=-y9=b,y12=-x9=-a+b;
ugyanis a-b is egész szám.
Az első négy sorban álló megoldás egymástól különböző, mert ennek feltétele (az első négy megoldás mintájára) x5≠y5, ami teljesül, mert b>0. Hasonlóan a második négyben x9≠y9, mert a>0. Annak feltételét kell még megkeresnünk, hogy a különböző négytagú megoldás‐csoportokban ne legyenek egyező megoldások.
x6=x1 ezért kell, hogy álljon y6≠y1, azaz
a-b≠b,másképpena≠2b.(4)


Hasonlóan x12=x2 ezért kell y12≠y2, azaz
-a+b≠a,azazb≠2a.(5)

 
 

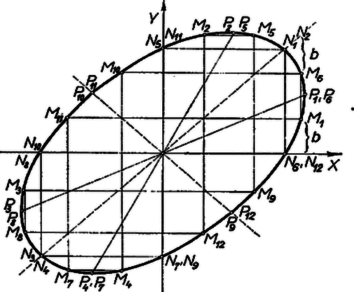Így az első csoport mindegyik megoldása különbözik mind a második, mind a harmadik csoport megoldásaitól. Nyilvánvaló ugyanis, hogy x-et és y-t egy pont derékszögű koordinátáinak tekintve az M3(x3,y3), M2(x2,y2) és M4(x4,y4) pontok az M1(x1,y1) pontból az origóra, ill. a tengelyek közti szögek szögfelezőire való tükrözéssel állnak elő, és a≠0, b≠0, valamint b≠a miatt a négy pont abszcisszája különböző. Továbbá az M1, M2, M3, M4 pontnégyes a fenti tükrözésekkel bármelyik pontjából kiindulva is előáll. Mindez a második és a harmadik csoport megoldásainak megfelelő pontnégyesekre is érvényes, ezért a közös abszcisszájú M6 és M1, valamint M12 és M2 pontpár tagjainak (4) és (5) szerinti különbözősége miatt az M6-ból és az M12-ből előálló pontnégyes különbözik M1, M2, M3, M4-től, és ez állításunkat bizonyítja.
Hasonlóan a második és harmadik csoport megoldásai különbözők, mert x5=x9, de y5≠y9. (Másképpen: a>b esetén ‐ amit nyilván feltehetünk ‐ a második csoport mindegyik megoldásában x és y értéke ugyanolyan előjelű, viszont a harmadik csoport összes megoldásaiban x és y értéke ellentett előjelű.)
Mindezek szerint ha az adott egyenletnek a feltétel szerinti megoldásában x és y értékei nem egyenlők, és egyik sem 2-szerese a másiknak, ‐ ez elegendő ahhoz, hogy az adott egyenletet legalább 12 egész számpár elégítse ki, a fent felsorolt megoldások.
 
 Szilágyi Tivadar (Budapest, Rákóczi F. g. III. o. t.)
 
Megjegyzések. 1. Ha a feltétel szerinti megoldásban a=b ‐ ami szerint (4) és (5) teljesül ‐, akkor a fenti xi, yi (i=1, 2, ..., 12) megoldásoknak megfelelő Ni pontok közül csak 6 különböző. Hasonlóan ha c2-cd+d2=n, c>0 és c=2d, akkor az a, b számpár helyén c, d-t véve a Pi(xi,yi) pontok között szintén csak 6 különböző. Ugyanazon n mellett ilyen a, b és c, d megoldás lehetetlen, mert az első esetben n=a2, négyzetszám, a másodikban viszont n=3d2, nem négyzetszám.
Megállapításunk nem azt mondja, hogy ha az adott egyenlet valamely (a,b) megoldására a=b, vagy a=2b, vagy b=2a, akkor az adott egyenlet egész megoldásainak száma kevesebb 12-nél, csupán azt, hogy ilyen megoldásból a fentiek szerint csak 5 további megoldást lehet leszármaztatni. Lehetséges ugyanis, hogy az a=b vagy a=2b feltételt teljesítő megoldáson kívül van más a (2), ill. (4), ill. (5) feltételt teljesítő megoldás is. Pl. n=72 esetén egy megoldás a=b=7, de megoldás a'=8, b'=3 is, továbbá n=3⋅72 esetén megoldás b=7, a=2b=14, de kielégíti az egyenletet a'=13, b'=2 is, így az x2-xy-y2=49 és az x2-xy-y2=147 egyenletek egész megoldásainak száma legalább 18.
2. A második és harmadik megoldáscsoporthoz a (3) átalakítások helyett az alábbi meggondolással is eljuthatunk. Az adott egyenlet x-re is, y-ra is másodfokú, ezért egyikük értékét megválasztva a másikra legfeljebb 2 megoldás van, s azok egyikét a feltevésből ismerve a másikat kiszámíthatjuk. Pl. tudva, hogy x=a mellett az egyik megoldás y=b, a másik az
a2-ay+y2=n,azazy2-ay+a2-n=0egyenletből
y=a-b, hiszen itt a két gyök összege a. Hasonlóan az y=b melletti, x=a-tól különböző gyök az x2-bx+b2-n=0 egyenletből x=b-a. Ezek szerint minden (x0,y0) megoldásból két új megoldást kapunk a következő két módon:
x'=x0,y'=x0-y0;x''=y0-x0,y''=y0,
hacsak y'≠y0, ill. x''≠x0. Kiindulva pl. a fenti M1 ponthoz tartozó megoldásból az első és második mód váltakozó alkalmazásával sorra a fenti M6, M10, M4, M7, M11 ponthoz tartozó megoldást kapjuk, majd M11-ből ismét M1-et. Hasonlóan kapcsolódnak egymáshoz az M2, M12, M8, M3, M9 M5, és az N1, N6, N8, N3, N7, N5 pontokhoz tartozó megoldások. Viszont P1-ből (x=2b, y=b) az első módon indulva önmagába jutunk.
3. Az adott egyenlet írható
(x+y2)22n+(x-y2)22n/3=1
alakban, eszerint annak az ellipszisnek az egyenletével van dolgunk, melynek középpontja az origó, nagy tengelye az X tengelyhez képest +45∘-kal van elfordulva, fél nagytengelye 2n, fél kistengelye 2n/3. Fentebb ennek az ellipszisnek az x=a, ill. y=b egyenessel való második metszéspontját határoztuk meg.