Feladat:	1240. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Bense Imre
Füzet:	1964/január, 12 - 14. oldal		PDF  |  MathML
Témakör(ök):	Ábrázoló geometria, Térfogat, Alakzatok mértéke, Térgeometria alapjai, Feladat
Hivatkozás(ok):	Feladatok: 1963/március: 1240. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     1. ábra   Állítsuk a testet az $ABCDEF$ szabályos hatszög‐lapra (1. ábra). Így könnyen belátjuk, hogy az alappal párhuzamos $GHJ$ szabályos háromszög‐lap szimmetriatengelyei benne vannak a hatszög szemközti oldalpárjainak felezőpontját összekötő három szimmetriatengelyen át állított függőleges síkban. Ha ugyanis a test egy négyzetlapja $ABHG$, vagyis $GH\parallel AB$, akkor a $GH$ él $K$ felezőpontja benne van az $AB$ él felező merőleges síkjában, így ez a sík a $GH$ élnek is felező merőleges síkja, tehát tartalmazza a $J$ csúcsot is. Így a további két négyzetlap $CDJH$ és $EFGJ$ lesz, a mondottak ezekre is érvényesek. Másrészt a test további háromszög‐lapjai $BCH$, $DEJ$ és $FAG$. Ezek szerint a testnek van 3 szimmetriasíkja és az alaplapok középpontjait összekötő tengely körüli ${360}^{\circ }/3$ nagyságú forgások önmagába viszik át. 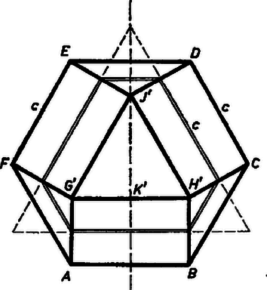    2. ábra   Legyen $G$, $H$, $J$ vetülete az alapsíkon $G\text{'}$, $H\text{'}$, $J\text{'}$ (2. ábra), és daraboljuk szét a testet a $G\text{'}H\text{'}J\text{'}$ háromszög oldalszakaszain, valamint az $AG\text{'}$, $BH\text{'}$, $CH\text{'}$, $DJ\text{'}$, $EJ\text{'}$ és $FG\text{'}$ szakaszokon át állított függőleges síksávokkal. Keletkezik a $G\text{'}H\text{'}J\text{'}$ alapú szabályos háromoldalú hasáb, három fekvő helyzetű, egymással egybevágó merőleges hasáb, derékszögű háromszög alaplappal, pl. $AGG\text{'}BHH\text{'}$, végül három egybevágó háromoldalú gúla, pl. $AFGG\text{'}$. Az utóbbiakat (párhuzamos eltolással) összetolva szabályos tetraédert kapunk. Élét $c$-vel, magasságát $m$-mel jelölve térfogata $c^{2}m/4\sqrt[]{3}$ (nincs szükség arra, hogy $m$-et kifejezzük $c$-vel). Az egybevágó hasábok alaplapjának befogói $m$ és $c/\sqrt[]{3}$, a szabályos háromszög magasságának $2/3$ része, oldalélük $c$, ezért együttes térfogatuk $c^{2}m\sqrt[]{3}/2$. Végül a szabályos háromoldalú hasáb térfogata $c^{2}m\sqrt[]{3}/4$, ennélfogva az egész testre $\begin{array}{c}{\displaystyle V=c^{2}m\left(\frac{1}{4\sqrt[]{3}}+\frac{\sqrt[]{3}}{2}+\frac{\sqrt[]{3}}{4}\right)=\frac{5c^{2}m}{2\sqrt[]{3}}\mathrm{.}}\end{array}$ (2) A vizsgálandó képletben $t_3=c^2\sqrt[]{3}/4$, $t_6=6t_3$. A magasság felező merőleges síkja a testből olyan hatszöget metsz ki, melynek mindegyik szöge $120{}^{\circ }$, és oldalai váltakozva $c$, ill. $c/2$ hosszúak. Ezért területét megkapjuk, ha egy $2c$ oldalú szabályos háromszög területéből kivonjuk három, egyenként $c/2$ oldalú szabályos háromszög területét: $\begin{array}{c}{\displaystyle T=\frac{\sqrt[]{3}}{4}\left[{\left(2c\right)}^2-3{\left(\frac{c}{2}\right)}^2\right]=\frac{13c^2\sqrt[]{3}}{16}=\frac{13}{4}{t}_3\mathrm{.}}\end{array}$ Így az (1)-beli zárójeles kifejezés értéke $t_6+4T+t_3=20$ $t_3=5\sqrt[]{3}{c}^2$, tehát az adott képlettel $\begin{array}{c}{\displaystyle V=\frac{m}{6}\cdot 5\sqrt[]{3}{c}^2=\frac{5m{c}^2}{2\sqrt[]{3}}\mathrm{,}}\end{array}$ egyezik (2)-vel. Az állítást bebizonyítottuk.    Bense Imre (Esztergom, Temesvári Pelbárt g. III. o. t.)   Megjegyzések. 1. A számításban nem használtuk ki lényegesen, hogy a szóban forgó test oldallapjai négyzetek és szabályos háromszögek, a számítás és az állítás akkor is érvényes, ha e lapok helyett egybevágó téglalapokat és egyenlő szárú háromszögeket veszünk. 2. Meg lehet mutatni, hogy az (1) képlet érvényes minden olyan konvex síklapú testre, melynek összes csúcsai két párhuzamos síkban feküsznek, ennélfogva oldallapjai háromszögek, két szomszédos háromszög együtt trapézt is alkothat (eszerint érvényes (1) csonka gúlákra is). Az ilyen testeket prizmatoidoknak nevezzük. Sőt bizonyos olyan görbe felületű testekre is érvényes (1), melyeket két párhuzamos síkban fekvő görbevonalú idom és egy görbe felület határol (pl. gömbréteg).