Feladat: 1237. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Kemenes János ,  Rejtő Lídia ,  Treer Mária 
Füzet: 1964/január, 10 - 12. oldal  PDF  |  MathML 
Témakör(ök): Trigonometria, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 1963/március: 1237. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tegyük fel, hogy a szokásos jelöléseket használva az A csúcsból húzott magasság A0 talppontja a BC oldal belsejébe esik, tehát 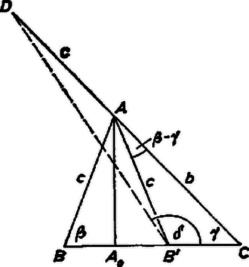β<90∘.

 
 
1. ábra
 

Legyen B-nek A0-ra vett tükörképe B' (1. ábra). Ez az A0C szakaszon van, mert A0B'A∢=A0BA∢=β>γ=A0CA∢. Az AB'C háromszögben a B'C oldal a vetületek különbsége, tehát 1 egység, az A csúcsnál levő szög β‐γ, és az A-ban összefutó oldalak összege AC+AB'=AC+AB=b+c. Írjuk fel e háromszög B'C oldalára a koszinusz‐tételt. c=5-b helyettesítéssel
1=b2+(5-b)2-2b(5-b)cos20∘,(1+cos20∘)b2-5(1+cos20∘)b+12=0,b=52+254-121+cos20∘≈2,5+6,25-6,187≈(1)≈2,5+0,063≈2,5+0,251=2,751egység, és ígyc=52-254-121+cos20∘≈2,249egység(2)


(a másik gyököt, ami az itt c-re nyert érték, mindjárt mellőztük, mert b<c-re vezet, ami β>γ miatt lehetetlen).
Az a oldal egyenlő a szóban forgó vetületek összegével: a=BA0+A0C. Ezért az AA0 magasságnak az ABA0 és ACA0 derékszögű háromszögekből vett kifejezéseit egyenlővé téve rendezés után egyenletet kapunk a-ra:
AA02=AB2-BA02=AC2-A0C2,A0C2-BA02=AC2-AB2,(BA0+A0C)(A0C-BA0)=(AC+AB)(AC-AB),


tehát (1) és (2) figyelembevételével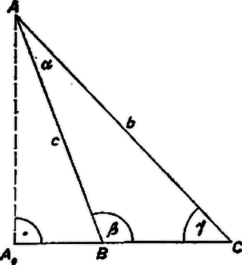
a⋅1=a=5⋅2254-121+cos20∘≈2,51egység.
Mindezek szerint az oldalak: a≈2,51, b≈2,751, c≈2,249 egység.
 
 
2. ábra
 

Ha A0 a BC oldal meghosszabbítására esik (b>c miatt a B-n túlra, 2. ábra), akkor b és c vetületeinek a különbsége maga a BC=a oldal, és ennek A-ból vett látószöge β‐γ helyett α, ami β≠90∘ esetében különbözik tőle. Ebben az esetben előző számításaink így nem alkalmazhatók. Megmutatjuk azonban, hogy ez az eset nem lehetséges.
A kizárandó esetben, β>90∘, γ>70∘ volna, tehát b>c>AA0=A0Ctgγ>BCtgγ=tgγ>tg70∘>2,7, és így b+c>2⋅2,7=5,4, ami lehetetlen, mert b+c=5. Eszerint fenti feltevésünk helyes.
 
 Rejtő Lídia (Budapest, Berzsenyi D. lg. III. o. t.)
 
Megjegyzés. A gyökjel alatti hányadost logaritmussal 4 értékes jegyre számítottuk ki, a különbségben azonban csak 2 értékes jegy maradt, ezért a négyzetgyökből 3-nál több értékes jegyet semmi esetre sem írhattunk ki. Közönséges osztással viszont a hányadosból 5 értékes jegyet írhatunk ki, mert az 1,9397 osztóban is 5 értékes jegy van, ezért a gyökjel alatt eggyel több jegyet kapunk:
6,25-6,1865=0,0635≈0,252;
így b≈2,752, c≈2,248, a≈2,52 egység.
 

II. megoldás. Felhasználjuk az I. megoldás második részéből, hogy β<90∘. Forgassuk rá az AB oldalt AC-nek A-n túli meghosszabbítására: AD=AB, így CD=b+c=5, és kössük össze D-t B'-vel (1. ábra). Az AB'D egyenlő szárú háromszögben ADB'∢=(β-γ)/2=10∘. Számítsuk ki a CB'D=δ szöget. A színusz‐tétellel
sinδ=5sin10∘,
másrészt δ>CB'A=180∘-β>90∘, ezért δ=119,78∘, és így B'CD∢=γ=50,22∘, β=70,22∘. Most már az AB'C háromszögből kiszámíthatjuk b-t és c-t, majd az eredeti háromszögből a-t. Ezzel a számítással elkerültük a koszinusz‐tétel felhasználását.
 
 Treer Mária (Budapest, Kaffka M. lg. II. o. t.)
 
Több megoldás goniometriai összefüggésekben használta fel a β‐γ különbséget. Egy ilyet vázol a
 
III. megoldás. Legyen a háromszög köré írt kör sugara R, így
b+c=2Rsinβ+2Rsinγ=2R(sinβ+sinγ)=4Rsinβ+γ2cos10∘=5.

Másrészt a b', c' vetületek különbsége (β<90∘ felhasználásával):
b'-c'=bcosγ-ccosβ=2R(sinβcosγ-sinγcosβ)=2Rsin(β-γ)==4Rsin10∘cos10∘=1.


Ezekből
sinβ+γ2=5sin10∘,β+γ2=60,22∘
(mert hegyes szög). Tovább a II. megoldás szerint haladhatunk.
 
Kemenes János (Budapest, Könyves Kálmán g. IV. o. t.)

 
Megjegyzés. A II. és III. megoldás egybevetéséből adódó (β+γ)/2=180∘-δ összefüggést elemi úton is megkaphatjuk:
180∘-δ=BB'D∢=BB'A∢-DB'A∢=β-β-γ2=β+γ2.