Kezdőlap


Feladat:	1232. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Naszályi Ferenc
Füzet:	1964/január, 9 - 10. oldal		PDF \| MathML
Témakör(ök):	Egyenes körhengerek, Egyenes körkúpok, Terület, felszín, Térfogat, Feladat
Hivatkozás(ok):	Feladatok: 1963/február: 1232. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kettős kúpon azt a felületet értjük, amelyet egy egyenes leír, ha egy metsző (de nem derékszögben metsző) egyenes körül forgatjuk, tehát a két, közönséges értelemben vett kúp csúcsa közös. A szimmetria miatt a felületet metsző két alapsík a közös csúcstól egyenlő távolságban van.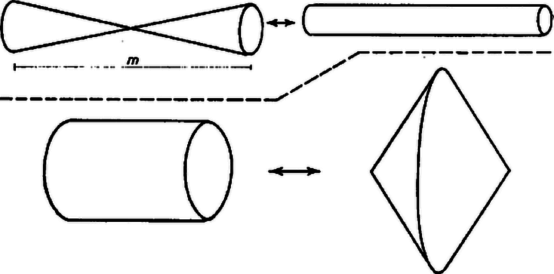

Legyen a henger alapjának sugara

r

, a kúp alapjáé

R

, közös magasságuk

m

, térfogatuk

V

, felszínük

F

. Így a két kúp oldalvonala is egyenlő, hosszuk

o = \sqrt[]{R^{2} + m^{2} / 4}

. A térfogatok egyenlőségéből

\begin{matrix} r^{2} π m = 2 \frac{R^{2} π m}{6}, R^{2} = 3 r^{2}, \end{matrix}

(mivel nyilván

m \neq 0

). A felszínek egyenlőségéből pedig

\begin{matrix} F = 2 r^{2} π + 2 r π m = 2 (R^{2} π + R π o) = 2 R^{2} π + R π \sqrt[]{4 R^{2} + m^{2}} . \end{matrix}

(1)

R

kiküszöbölése, egyszerűsítések, majd négyzetre emelés után az adódó másodfokú egyenlet negatív gyökét mindjárt mellőzve

\begin{matrix} 2 m - 4 r = \sqrt[]{36 r^{2} + 3 m^{2},} \\ r = m \frac{\sqrt[]{21} - 4}{10} \approx 0, 0583 m, \end{matrix}

és ebből

\begin{matrix} R = m \frac{3 \sqrt[]{7} - 4 \sqrt[]{3}}{10} \approx 0, 1009 m, V = \frac{m^{3} π}{100} (37 - 8 \sqrt[]{21}) \approx 0, 01055 m^{3}, \\ F = \frac{m^{2} π}{50} (2 \sqrt[]{21} - 3) \approx 0, 387 m^{2} . \end{matrix}

Naszályi Ferenc (Budapest, Kölcsey F. g. IV. o. t.)

Megjegyzés. Többen a 292. fizikai feladat szemléletéből kiindulva a két kúpot az alapjukkal összeillesztve gondolták. Ekkor (1) jobb oldalán a

2 R^{2} π

tag elmarad és hasonló számítással a következő eredmények adódnak:

\begin{matrix} r = m \frac{\sqrt[]{3} + 1}{8} \approx 0, 342 m, & R = \frac{3 + \sqrt[]{3}}{8} m \approx 0, 717 m, \\ V = \frac{m^{3} π}{32} (2 + \sqrt[]{3}) \approx 0, 365 m^{3}, & F = \frac{m^{2} π}{16} (6 + 5 \sqrt[]{3}) \approx 2, 88 m^{2} . \end{matrix}