| Feladat: | 1224. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Dobó Ferenc , Fejéregyházi Sándor , Folly Gábor , Földes Antónia , Hermann I. , Komor Tamás , Kovács L. , Lakó Ferenc , Lehel Jenő , Lovász László , Makai Endre , Markó J. , Mészáros György , Nagy Péter Tibor , Nárai György , Papp M. , Pelikán József , Somos P. , Somos Péter , Székely G. , Székely Gábor , Szilágyi Tibor , Szilágyi Tivadar , Tamás Endre , Veres Ferenc | ||
| Füzet: | 1963/december, 202 - 203. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorikus geometria síkban, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1963/január: 1224. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Szorítkozzunk eleve az esetre. A szomszédos osztópontok távolságát válasszuk egységnek. A kezdőponttól indulva az egymás utáni kiragadott pontok távolsága a megelőzőtől legyen sorra , , , . Ezek összege . Ha van köztük két egyenlő, akkor az állítás igaz, feltehetjük tehát, hogy mind különbözők. Ekkor összegük legalább , ami éppen megegyezik a pontsor hosszával, tehát , , , , az 1, 2, , értékekkel egyenlő valamilyen sorrendben. II. megoldás. Jelöljük az részre osztott szakasz végpontjait , -vel. Az kiragadott pont által kifeszített szakaszok száma is , mert az egyik végpontot -féleképpen választhatjuk, a másikat a maradó pont közül -féleképpen, az így adódó megválasztásban azonban minden szakasz kétszer szerepel, ti. a végpontok megcserélésével. Így csak akkor lehet minden szakasz különböző, ha 1-től -ig minden érték fellép, mint szakasz hossza. 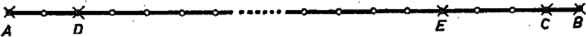 hosszúságú maga az szakasz. hosszúságú szakaszt csak az egyik végponttól ‐ jelöljük ezt -val ‐ a másik előtti osztópontig jelölhetünk ki. Most már az hosszúság kijelölését nem kezdhetjük -tól, mert akkor a előtti osztópontot is ki kellene választanunk, és így két db egységnyi szakasz adódna, sem ugyanilyen okból az melletti osztóponttól, így csak az utáni második osztóponttól -ig terjedő szakasz lehet a kiválasztott hosszúságú szakasz. Ezzel egyszersmind ki van jelölve egy hosszúságú szakasz is: és egy 2 hosszúságú: . Nem választható most már ki a -t követő első két osztópont, sem a -t megelőző kettő, így a kiválasztott hosszúságú szakasz csak az -tól a előtti negyedik osztópontig, -ig terjedő szakasz lehet, a többi hosszúságú szakasznak legalább az egyik végpontja nem kiválasztható. Az kiválasztásával létrejött többi szakasz hossza: , , . Így nem kiválasztható a -t követően két további pont és az -t megelőző négy osztópont sem. Ezzel azonban minden az osztópontok közti hosszúságú szakasznak legalább egyik végpontját kizártuk. Eszerint a kívánt kiválasztás legfeljebb akkor lehetséges, ha szerepel a már kijelölt 1, 2, 3, 4 hosszúságok közt: , . Mivel -re már , így kell legyen a feladat állításának megfelelően. |