Kezdőlap


Feladat:	1222. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csirik János , Dobó Ferenc
Füzet:	1963/november, 126 - 130. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Oldalfelező merőleges, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1963/január: 1222. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az $a$ , $b$ , $c$ hosszúságú oldalakkal szemközti csúcsokat $A$ , $B$ , $C$ -vel, az ezeknél fekvő szögeket $α$ , $β$ , $γ$ -val, az oldalak felező pontjait $A_{1}$ , $B_{1}$ , $C_{1}$ -gyel, a $t_{a}$ , $t_{b}$ , $t_{c}$ szakaszok másik végpontját $D$ , $E$ , $F$ -fel. $A$ közelebb van $B$ -hez, mint $C$ -hez (mert $c < b$ ), ezért $B C$ felező merőlegesének arra az oldalára esik, mint $B$ , tehát a felező merőleges az $A C$ szakaszt metszi, vagyis $D$ az $A C$ oldalon van. Hasonlóan $a = B C > A C = b$ és $a = B C > B A = c$ következtében $E$ és $F$ az $a$ hosszúságú $B C$ oldalon van.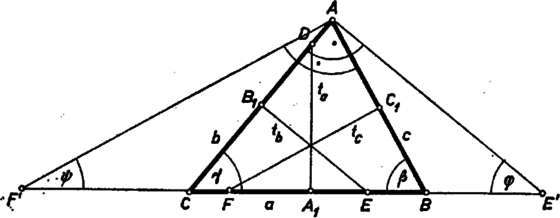

1. ábra

t_{a} = A_{1} D

és

t_{b} = B_{1} E

szakaszok az

A_{1} C D

és

B_{1} C E

derékszögű háromszögek közös

γ

szögével szemben levő befogók. A két háromszög hasonló, és mivel a

γ

szög melletti befogókra

\begin{matrix} C A_{1} = a / 2 > b / 2 = C B_{1}, \end{matrix}

így a másik befogó párra

t_{a} > t_{b}

áll fenn.
Húzzunk

t_{b}

és

t_{c}

összehasonlítására

A

-ból párhuzamost ezekkel, messék a párhuzamosok a

B C

egyenest az

E'

ill.

F'

pontban. Ekkor

B_{1} E

A C E'

háromszög középvonala,

C_{1} F

A B F'

-é, így

A E' = 2 B_{1} E = 2 t_{b}

A F' = 2 C_{1} F = 2 t_{c}

. Megmutatjuk, hogy az

A E' F'

háromszögben

E'

-nél nagyobb szög van, mint

F'

-nél. Ebből már következik, hogy

2 t_{c} = A F' > A E' = 2 t_{b}

t_{c} > t_{b}

, vagyis a feladat állításában szereplő második egyenlőtlenség.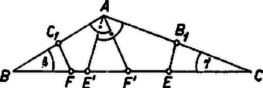

2. ábra

A C E'

és

A B F'

derékszögű háromszögekből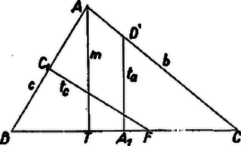

\begin{matrix} φ = A E' C ∢ = 90^{\circ} - γ, ψ = A F' B ∢ = 90^{\circ} - β, \end{matrix}

mivel továbbá

a > b > c

-ből következik, hogy

β

γ

hegyesszögek és

β > γ

, így

φ > ψ

. A szakaszokra vonatkozó egyenlőtlenség tehát igazolást nyer, ha belátjuk, hogy az

A E' F'

háromszög

E'

-nél és

F'

-nél levő szögei

φ

és

ψ

(és egyik esetben sem a

180^{\circ}

-ra kiegészítő szög). Ehhez meg kell még mutatnunk, hogy

E'

-től

C

és

F'

egy irányban van,

F'

-től pedig

B

és

E'

. Hegyesszögű háromszög esetében ez világos, mert

E'

B C

oldal

B

-n túli meghosszabbítására esik,

F'

pedig az oldal

C

-n túli meghosszabbítására. Ha

B A C

tompaszög, akkor

A E'

ennek a szögtartománynak a belsejében halad,

A B

-vel hegyesszöget zár be, így az

A B

-re merőleges

A F'

C A E'

szögtartomány belsejében halad, tehát a

B C

egyenessel való

F'

metszéspontja

E'

és

C

közé esik. Ezzel az egyenlőtlenségek bizonyítását befejeztük.

3. ábra

Húzzuk meg a háromszög

A

-ból induló

A T = m

magasságát. Mivel

a

a háromszög legnagyobb oldala,

T

az oldal belső pontja. A keletkező

A C T

háromszög hasonló

D C A_{1}

-hez, az

A B T

háromszög pedig

F B C_{1}

-hez, mivel a háromszögek derékszögűek és

C

-nél, ill.

B

-nél közös szögük van.
Alkalmazva Pythagorász tételét az

A B T

és

A C T

háromszögekre

\begin{matrix} c^{2} = m^{2} + B T^{2}, b^{2} = m^{2} + C T^{2}, \end{matrix}

a két egyenlet különbségét képezve

\begin{matrix} b^{2} - c^{2} = C T^{2} - B T^{2} = (C T + B T) (C T - B T) = a (C T - B T) . \end{matrix}

A C T

és

D C A_{1}

háromszög hasonlóságából

\begin{matrix} C T = \frac{A T}{A_{1} D} C A_{1} = \frac{m}{t_{a}} \cdot \frac{a}{2}, és C T - B T = 2 C T - a = \frac{m}{t_{a}} a - a, \end{matrix}

így

\begin{matrix} b^{2} - c^{2} = a (\frac{m a}{t_{a}} - a) . \end{matrix}

(1)

Hasonlóan az

A B T

és

F B C_{1}

háromszögek hasonlóságából

\begin{matrix} B T = \frac{A T}{F C_{1}} B C_{1} = \frac{m}{t_{c}} \cdot \frac{c}{2}, és C T - B T = a - 2 B T = a - \frac{m c}{t_{c}}, \end{matrix}

így

\begin{matrix} b^{2} - c^{2} = a (a - \frac{m c}{t_{c}}) . \end{matrix}

(2)

Ha fennáll,

t_{a} = t_{c}

, akkor

\begin{matrix} a = C T + T B = \frac{m a}{2 t_{a}} + \frac{m c}{2 t_{c}} = \frac{m}{2 t_{a}} (a + c), \end{matrix}

és így

\begin{matrix} \frac{m}{t_{a}} = \frac{2 a}{a + c} . \end{matrix}

Ezt (1)-be helyettesítve

\begin{matrix} b^{2} - c^{2} = a (\frac{2 a^{2}}{a + c} - a) = \frac{a^{2} (a - c)}{a + c}, \end{matrix}

(3)

vagy a törtet eltávolítva és

0

-ra redukálva

\begin{matrix} a^{3} - a^{2} c - a (b^{2} - c^{2}) - c (b^{2} - c^{2}) = 0. \end{matrix}

(4)

Ha van olyan háromszög adott

b

és

c

(b > c > 0)

mellett, amelyben két oldal

b

és

c

hosszúságú, a harmadik hossza ezeknél nagyobb, és

t_{a} = t_{c}

, akkor van olyan

a

érték

b

és

b + c

közt, amelyre (4) teljesül.
Megfordítva: ha teljesül (4) egy

b

és

b + c

közti

a

értékre, akkor egyrészt

a + c > 0

, és így teljesül (3) is.
Másrészt minden háromszögre teljesül (1) és (2). Ezek és (3) összehasonlításából egyrészt

\begin{matrix} \frac{m a}{t_{a}} - a = \frac{2 a^{2}}{a + c} - a, \frac{m}{t_{a}} = \frac{2 a}{a + c}, \end{matrix}

másrészt

\begin{matrix} a - \frac{m c}{t_{c}} = \frac{a (a - c)}{a + c}, \frac{m}{t_{c}} = \frac{1}{c} [a - \frac{a (a - c)}{a + c}] = \frac{2 a}{a + c}, \end{matrix}

tehát

t_{a} = t_{c}

.
Azt kell tehát belátnunk, hogy az

\begin{matrix} f (x) = x^{3} - x^{2} c - x (b^{2} - c^{2}) - c (b^{2} - c^{2}) \end{matrix}

polinomnak van

b

és

b + c

közé eső gyöke.
Írjunk az egyenlet bal oldalán

x

helyére előbb

b

-t, majd

b + c

-t:

\begin{matrix} f (b) & = - 2 b^{2} c + b c^{2} + c^{3} = - c (b - c) (2 b + c) < 0, \\ f (b + c) & = 2 c^{2} (b + c) > 0, \end{matrix}

ellentett előjelűek. Ezek szerint adott pozitív

b

c

értékek és

b > c

esetén van olyan

a

szám, amelyre

\begin{matrix} b < a < b + c, \end{matrix}

másrészt

f (a) = 0

. Így az

a

b

c

oldalak háromszöget adnak, és abban

t_{a} = t_{b}

, mert a végzett számítás visszafordítható.

Az egyenlőtlenségek bizonyítása Dobó Ferenc (Budapest, I. István g. IV. o. t.) dolgozatából.

II. megoldás. A szögek fenti jelöléseivel a megfelelő derékszögű háromszögekből

\begin{matrix} t_{a} = \frac{a}{2} tg γ, t_{b} = \frac{b}{2} tg γ, t_{c} = \frac{c}{2} tg β . \end{matrix}

(5)

Így az

a / 2 > b / 2

egyenlőtlenséget a pozitív

tg γ

-val szorozva

t_{a} > t_{b}

.
Másrészt

γ < β < 90^{\circ}

miatt

cos γ > cos β > 0

, és

\begin{matrix} 0 < \frac{1}{cos γ} < \frac{1}{cos β} . \end{matrix}

Ezt a színusz tételből adódó, pozitív tagokból álló

\begin{matrix} \frac{b sin γ}{2} = \frac{c sin β}{2} \end{matrix}

egyenlőséggel szorozva

t_{b} < t_{c}

adódik.
A

t_{a} = t_{c}

követelményből a szögfüggvényeket az oldalakkal kifejezve egyenletet kapunk

a

-ra.

\begin{matrix} tg γ & = \frac{sin γ}{cos γ} = \frac{2 a b sin γ}{a^{2} + b^{2} - c^{2}} = \frac{4 t}{a^{2} + b^{2} - c^{2}} és \\ tg β & = \frac{4 t}{a^{2} + c^{2} - b^{2}}, \end{matrix}

ezért behelyettesítéssel és a szokásos rendezési lépésekkel:

\begin{matrix} \frac{a}{a^{2} + b^{2} - c^{2}} = \frac{c}{a^{2} + c^{2} - b^{2}}, \\ a^{3} - c a^{2} - (b^{2} - c^{2}) a - (b^{2} - c^{2}) c = 0. \end{matrix}

(A nevezők egyike sem 0, mert csak a

b

és

c

-nél nagyobb

a

értékekre szorítkozunk.) Ezzel ismét az I. megoldás (4) egyenletére jutottunk.

Az egyenlőtlenségek bizonyítása Csirik János (Orosháza, Táncsics M. g. III. o. t.) dolgozatából.

Megjegyzés. A dolgozatok a

t_{a} = t_{c}

követelményből az (5) kifejezésekkel és a színusz‐tétel alkalmazásával levezették az

\begin{matrix} a = b \cdot \frac{cos γ}{cos β} \end{matrix}

(6)

összefüggést, és ebből következtettek egy a

b

-nél nagyobb

a

létezésére, a

cos γ > cos β (> 0)

egyenlőtlenség felhasználásával. Ez nem helyes, mert burkoltan felhasználták a bizonyítandó állítást.

γ

-ról és

β

-ról csak akkor beszélhetünk, ha már tudjuk, hogy létezik olyan

a

, amely

b

-vel és

c

-vel együtt háromszöget alkot és abban

t_{a} = t_{c}

. Még világosabban:

b

β

és

γ (< β)

megadásával a háromszög már meg van határozva, és nem biztos, hogy teljesül (6).