Kezdőlap


Feladat:	1216. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Makai Endre
Füzet:	1963/november, 117 - 119. oldal		PDF \| MathML
Témakör(ök):	Euler-féle poliédertétel alkalmazásai, Euler-formula, Térgeometria alapjai, Feladat
Hivatkozás(ok):	Feladatok: 1962/december: 1216. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1175. feladatban¹ beláttuk (az éleket egyrészt a lapok, másrészt a csúcsok szerint számlálva össze és felhasználva Euler poliéder‐tételét), hogy a feladat feltételei mellett az ötszöglapok száma 12, függetlenül attól, hány hatszög határlap van.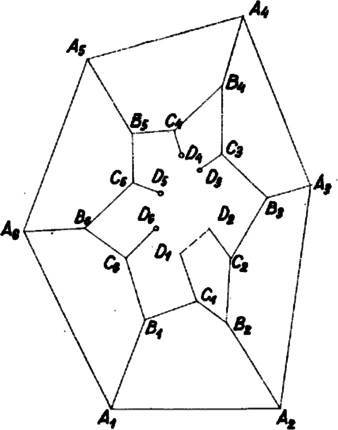

1. ábra

Feltéve, hogy fellép hatszög is a határlapok között, be kell látnunk, hogy fel kell lépnie legalább kettőnek. Megkísérlünk felépíteni egy 13 lapú testet 12 ötszög és egy hatszög határlappal és belátjuk, hogy ez lehetetlen. Ha megpróbálunk felvázolni egy ilyen poliédert kiindulva pl. a hatszög lapból, akkor gondolni kell arra a lehetőségre, hogy a fellépő újabb és újabb csúcsok közt lehetnek egymással, vagy egy már korábban felvett csúccsal egybeesők is.
Ilyen egybeesések kizárására sok lehetőséget nyújt az a kikötés, hogy a test minden csúcsába 3 él fut. Ennek folytán
(1) 3 összefutó él nem lehet egy síkban;
(2) ha két lapnak van közös csúcsa, ebből indul egy közös él is;
(3) bármely két közös végpontú él valamelyik határlap két szomszédos oldala is.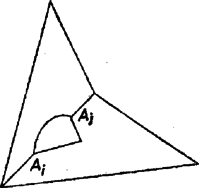

2. ábra

Tegyük fel, hogy léteznék a szóban forgó poliéder. Legyen

A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}

a hatszög lapja. Ennek mindegyik csúcsából kiindul egy

A_{i} B_{i}

él

(i = 1

, 2,

...

, 6). Itt

B_{i}

(1) szerint nincs a hatszög síkjában, tehát különbözik az

A_{j}

-ktől, de különbözik a többi

B_{j}

-ktől is. Ugyanis ha két szomszédos hatszögcsúcsból induló él,²

A_{i} B_{i}

és

A_{i + 1}

B_{i + 1}

egy csúcsba futna (

B_{i} = B_{i + 1}

volna), akkor a keletkező

A_{i} A_{i + 1} B_{i}

háromszög határlapja volna a poliédernek, de annak nincs háromszög lapja. Két nem szomszédos hatszögcsúcsból:

A_{i}

-ből és

A_{j}

-ből induló élnek pedig azért nem lehet közös a másik végpontja, mert akkor (3) szerint a poliédernek ugyanazt a határlapját kellene határolniuk, de akkor az utóbbi határlapnak (2) szerint két közös éle is volna a hatszöggel, egy

A_{i}

-ből és egy

A_{j}

-ből induló, ami konvex poliédernél nem lehetséges.
Az

A_{i} A_{i + 1}

élhez csatlakozik egy ötszög. Ennek

A_{i}

-vel, ill.

A_{i + 1}

-gyel szomszédos csúcsa csak

B_{i}

, ill.

B_{i + 1}

lehet, mert csak ezekből fut ‐ hatszög csúcsokon kívül ‐

A_{i}

-be, ill.

A_{i + 1}

-be él. Jelöljük az ötszög ötödik (

B_{i}

-vel és

B_{i + 1}

-gyel szomszédos) csúcsát

C_{i}

-vel (

i = 1

, 2,

...

, 6). Ez különbözik az ötszög többi csúcsától és a hatszög csúcsaitól is (hiszen egy konvex test két határlapjának nem lehet 3 közös csúcsa). Különbözik a

B_{j}

csúcsoktól is, ezt

B_{i}

B_{i + 1}

-re már láttuk. Ha

C_{i}

egy másik

B_{j}

csúccsal esne egybe, akkor össze lenne kötve az

A_{i}

-től és

A_{i + 1}

-től különböző

A_{j}

csúccsal. Ekkor volna (3) szerint a poliédernek egy

B_{i + 1}

C_{i}

A_{j}

-n átmenő lapja, ennek volna egy a hatszöggel közös

A_{j} A_{k}

éle és egy ehhez csatlakozó

A_{k} B_{k}

éle, mivel a szóban forgó határlap nem lehet a hatszög. Ez a határlap ötszög kell, hogy legyen, tehát

B_{k}

különbözik

B_{i + 1}

-től és össze van vele kötve. Ez azonban lehetetlen, mert a

B

csúcsokból csak

A

- és

C

-csúcsba megy él.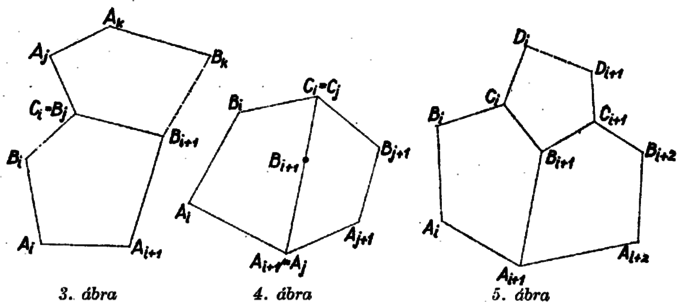

Két különböző

C_{i}

C_{j}

csúcs sem eshet egybe, különben az

A_{i} B_{i} C_{i} B_{i + 1} A_{i + 1}

és

A_{j} B_{j} C_{j} B_{j + 1} A_{j + 1}

lapoknak egy

C_{i}

-ből, ill.

C_{j}

-ből induló éle egybeesne, tehát

B_{i}

B_{i + 1}

egyike

B_{j}

B_{j + 1}

valamelyikével azonos volna. Mivel

i \neq j

és a

B

csúcsok mind különbözők, így

i = j + 1

, vagy

j = i + 1

kellene hogy legyen. Ez azonban

C_{i} = C_{j}

-vel együtt azt jelentené, hogy két szomszédos határlap két egymás utáni élben érintkezne, ami nem lehetséges.
A

C_{i}

pontokból ismét ki kell indulnia még egy‐egy

C_{i} D_{i}

élnek (

i = 1

, 2,

...

, 6). A

D_{i}

végpont nem eshetik egybe egyik

A_{j}

-vel sem, mert az utóbbiból csak

A

és

B

pontokba fut él, és

C

-be nem;

D_{i}

B_{j}

csúcsoktól is különbözik, mert közülük

B_{i}

-be és

B_{i + 1}

-be fut él

C_{i}

-ből,

C_{i} D_{i}

pedig az ezektől különböző,

C_{i}

-ből induló él.
A

D_{i}

C_{i}

B_{i + 1}

C_{i + 1}

D_{i + 1}

csúcsok ebben a sorrendben egy határlap csúcsai, ugyanis az

A_{i} B_{i} C_{i} B_{i + 1} A_{i + 1}

laphoz a

C_{i} B_{i + 1}

él mentén csatlakozó lapnak az éllel szomszédos csúcsai csak

D_{i}

, ill.

C_{i + 1}

lehetnek. Ez tehát egyben az

A_{i + 1} B_{i + 1} C_{i + 1} B_{i + 2} A_{i + 2}

laphoz

B_{i + 1} C_{i + 1}

mentén csatlakozó lap is, aminek

C_{i + 1}

-gyel szomszédos csúcsa

D_{i + 1}

. Mivel ez a határlap csak ötszög lehet,

D_{i}

-t él köti össze

D_{i + 1}

-gyel.
A

D_{i}

csúcsoknak különbözniük kell a

C_{j}

csúcsoktól is, mert előbbi

C_{i}

D_{i - 1}

D_{i + 1}

-gyel van összekötve, utóbbi

B_{j}

B_{j + 1}

D_{j}

-vel, és beláttuk, hogy az előbbi 3 csúcs közt nem szerepel

B

csúcs.
Ezzel felsoroltuk a test mind a 13 lapját, tehát a

D_{i} D_{i + 1}

élek közt kell egybeesőknek lenniük úgy, hogy a test záruljon.

D_{i}

és

D_{i + 2}

különbözők, mert két szomszédos határlap nem érintkezhet két szomszédos él mentén.

D_{i}

és

D_{i + 3}

sem eshet egybe, mert különben a

D_{i} D_{i + 1} D_{i + 2}

(D_{i + 3} = D_{i})

háromszög egy további határlapja volna a poliédernek. Ezzel minden lehetőséget számba vettünk, mert két

D

csúcs vagy szomszédos (az indexezés sorrendjében), vagy második vagy harmadik szomszéd. Beláttuk ezzel, hogy nincs olyan konvex poliéder, amelyet egy hatszög és 12 ötszög határolna.

Makai Endre (Budapest, Eötvös J. g. II. o. t.)
dolgozata, kiegészítésekkel

Megjegyzés. Két helyen hivatkoztunk a test konvex voltára: a második bekezdés végén és a harmadik elején, de mindkettő helyettesíthető volna olyan meggondolással (ha kissé hosszabb is volna), amelyik csak arra hivatkozik, hogy minden csúcsba 3 él fut. Így az állítás helyes marad, ha a poliéder konvex volta helyett csak annyit teszünk fel, hogy teljesül rá az Euler‐tétel.

A versenyzők nem gondoltak egybeesési lehetőségekre a poliéder felépítése során egymás után felvett csúcsok között.

¹K. M. L. 25 (1962/11) 134. o.

²Itt és a továbbiakban, ha fellép 6-nál nagyobb index, ahelyett mindig 6-tal kisebb érték értendő.