Kezdőlap


Feladat:	1212. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Fejéregyházi Sándor
Füzet:	1964/február, 52 - 54. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Síkgeometriai számítások trigonometriával, Feladat
Hivatkozás(ok):	Feladatok: 1962/december: 1212. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A két érintkező kör sokféleképpen helyezkedhet el a háromszöghöz képest, és sokféleképpen választhatjuk meg a háromszöget meghatározó adatokat is. Oldjuk meg először a feladatot abban a legkézenfekvőbb esetben, ha mindkét kör a háromszög belsejében van (1. ábra), sugaruk $r$ , és érintik az $A B = c$ oldalt. A $T_{1}$ , $T_{2}$ érintési pontokkal 3 részre osztott oldalból

\begin{matrix} r ctg \frac{α}{2} + 2 r + r ctg \frac{β}{2} = c, r = \frac{c}{ctg \frac{α}{2} + ctg \frac{β}{2} + 2} . \end{matrix}

(1)

1. ábra

A O_{1}

és

B O_{2}

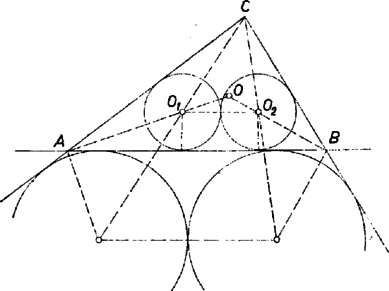egyenesek a beírt kör

O

középpontjában metszik egymást, és hasonlóan számíthatjuk a beírt kör

ϱ

sugarát, a nyert kifejezés alapján pedig a fenti nevező első két tagjának összegét:

\begin{matrix} ϱ = \frac{c}{ctg \frac{α}{2} + ctg \frac{β}{2}}, és így r = \frac{c}{\frac{c}{ϱ} + 2} = \frac{c ϱ}{c + 2 ϱ} . \end{matrix}

(2)

r

utóbbi kifejezését abból is megkaphatjuk, hogy az

A B O

háromszög területét felírjuk mint az

A B O_{2} O_{1}

, trapéz és az

O_{1} O_{2} O

háromszög területének összegét: a trapéz magassága

r

, és

O_{1} O_{2} = 2 r

.
Írható (2) a következő tetszetős alakban is:

\begin{matrix} \frac{1}{r} = \frac{c + 2 ϱ}{c ϱ} = \frac{1}{ϱ} + \frac{2}{c} . \end{matrix}

Innen látjuk, hogy a körpár ilyen típusú beírása esetén akkor kapunk legnagyobb sugarat, ha a körök közös érintőjének a leghosszabb oldalt választjuk, viszont a legrövidebb oldalt érintő körpár sugara a legkisebb.
(2)-t

s

-sel (a fél kerülettel) bővítve és

2 ϱ s = 2 t = c m_{c}

figyelembevételével

\begin{matrix} r = \frac{c t}{c s + 2 t} = \frac{t}{s + m_{c}} = \frac{c \sqrt[]{(s - a) (s - b) (s - c)}}{c \sqrt[]{s} + 2 \sqrt[]{(s - a) (s - b) (s - c)}} \end{matrix}

(kisebb magassághoz nagyobb

r

, és természetesen nagyobb alap tartozik). Az utolsó kifejezés

r

-et kizárólag az oldalak függvényeként állítja elő.
Bemutatjuk a két kör néhány különböző elhelyezkedését anélkül, hogy teljes felsorolást adnánk.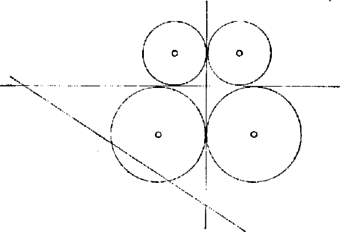

2. ábra

A két körnek a háromszög oldalain 4 érintési pontja kell hogy legyen (legalább), ezek közül legalább 2-nek egy oldalon kell lennie (ezek egybe is eshetnek), vagyis a háromszög egyik oldala a két kör közös érintője. Ez lehet az érintkezési pontjukban húzott érintő, és lehet egy külső közös érintő. Lehetséges az is, hogy mindkettő szerepeljen az oldalak között. Ekkor derékszögű a háromszög, és az átfogója tetszés szerinti egyenes lehet, vagy ha a derékszögű háromszögből indulunk ki, ahhoz tetszés szerinti nagyságú körpár írható úgy, hogy mindkettő érintse mindkét befogó egyenesét (az egyik érintheti emellett az átfogó egyenesét is, 2. ábra).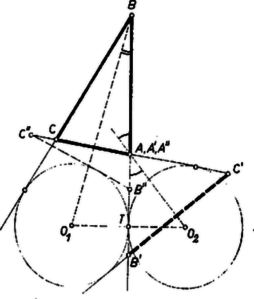

3. ábra

A közös belső érintő mellett a másik két oldalt alkothatja a körök egy‐egy további érintője (3. ábra). A körök eshetnek a háromszög valamelyik szögtartományába, egy ilyen szög csúcsszögének a tartományába, vagy a háromszög egy külső szögének a tartományába. A 3. ábra

A B C

háromszögének adataiból meghatározzuk alább a körök

r

sugarát. A szaggatott vonalak további lehetséges érintőket mutatnak. Ezek az

A B C

háromszög két-két megfelelő oldalegyenesével ismét egy‐egy olyan háromszöget alkotnak, melynek az adott körök 2‐2 oldalát érintik.
Ha a háromszög egyik oldala a két kör közös külső érintője, akkor is eshetnek a körök a háromszöghöz képest különböző tartományokba. Az 1. ábra feltüntet a beírt körpáron kívül még egy körpárt. Néhány további példát a 4. ábra mutat.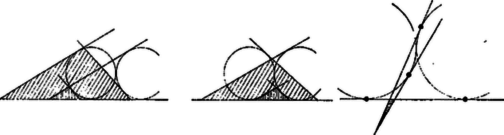

4. ábra

Az olvasóra bízzuk az összes lehetséges esetek felkutatását. Ezekre

r

a fentiekhez hasonlóan határozható meg és (1)-hez hasonló kifejezések adódnak azzal, hogy a nevezőben

ctg

helyett

tg

léphet fel és az előjelek változhatnak, ‐ a harmadik tagé is.

Térjünk most vissza a 3. ábra esetére. Itt

\begin{matrix} B A + A T = B T, c + r ctg \frac{α}{2} = r ctg \frac{β}{2}, és innen r = \frac{c}{ctg \frac{β}{2} - ctg \frac{α}{2}} . \end{matrix}

Lényeges különbség (1)-hez képest a nevezőben a 2-es tag hiánya.

Fejéregyházi Sándor (Budapest, I. István g., IV. o. t.)