Feladat: 1207. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Makai Endre ,  Nárai György ,  Veres Ferenc 
Füzet: 1963/november, 115 - 117. oldal  PDF  |  MathML 
Témakör(ök): Magasságpont, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):Feladatok: 1962/november: 1207. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Kizárjuk az olyan eseteket, ha van az e, f, g egyenesek között olyan, amely merőleges a másik kettő síkjára; ekkor ugyanis e1, f1 és g1 közül legalább az egyik pont, így a feladat értelmét veszti. Minden más esetben e1, f1, g1 különböző egyenesek, mert az e,f, az f,g és g,e síkok különbözők, a 3 síknak csak egy közös pontja van, legyen az O. Az e egyenes egy E pontjából f1-re és g1-re bocsátott merőlegesek feltétel szerint metszik 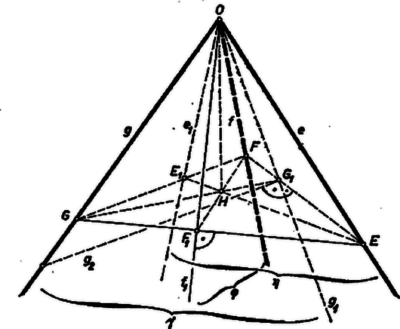g-t, ill. f-et.

 
 
1. ábra
 

Megmutatjuk, hogy FG merőleges az e,e1 egyenesek η síkjára; ebből már következik, hogy a kérdésre ,,igen'' a válasz, mert így FG merőleges az η sík minden egyenesére. Messe az EG egyenes f1-et F1-ben, EF a g1-et G1-ben. Azt állítjuk, hogy a g,g1 egyenesek γ síkja merőleges EF-re. OG1 és EF szerkesztés szerint merőlegesek, elég tehát belátnunk, hogy γ tartalmaz egy az EF-re merőleges, egyszersmind az OG1-gyel nem párhuzamos egyenest is. Ilyen a G1-ben az e,f síkra állított g2 merőleges, mert e,f tartalmazza EF-et, másrészt g2 merőleges g1-re, végül g2-n átmegy minden a G1-et tartalmazó és e,f-re merőleges sík, tehát γ is. Így valóban γ merőleges EF-re. Hasonlóan az f,f1=φ sík merőleges EG-re.
Az FF1 és GG1 egyenesek az EFG síkban vannak, tehát metszik egymást egy H pontban. Így egyrészt OH a φ és γ síkok metszésvonala, ezért merőleges EG és EF mindegyikére, egyszersmind az EFG síkra; tehát az ebben fekvő FG egyenesre is. Másrészt az EFG háromszögben FF1 és GG1 magasságvonalak, H a magasságpont, ezért EH mint a harmadik magasságvonal, ugyancsak merőleges FG-re. Legyen EH és FG metszéspontja 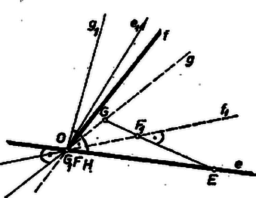E1.
 
 
2. ábra
 

Ezek szerint az OHE=OE1E=η* sík és a benne fekvő OE=e egyenes is merőleges FG-re. Ebből egyrészt OE1⊥FG következik, másrészt az, hogy η* merőleges az FOG=f,g síkra, ugyanis ez átmegy FG-n, és két sík akkor merőleges egymásra, ha egyikük tartalmaz egy a másikra merőleges egyenest. Azonban feltevésünk szerint az OE=e egyenes nem merőleges az f,g síkra, ezért rajta csak egy az f,g-re merőleges sík fektethető. Így η* azonos az e vetítéséhez használt η síkkal, és η-nak az f,g-vel való OE1 metszésvonala azonos e-nek e1 vetületével; tehát e1⊥FG. Ezt akartuk bizonyítani.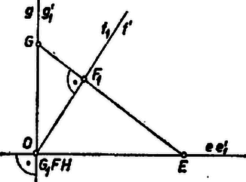
 
 
3. ábra
 

Ha e merőleges az f és g egyikére, pl. g-re (f-re azonban nem, 2. ábra, a térbeli helyzetnek az e,g síkon levő vetülete a 3. ábra), akkor g1 is merőleges e-re (g1-nek az e,g síkon levő vetülete azonos g-vel), ezért F az O-ba esik, így FG=g, ami merőleges e1-re. Érvényesek azonban előző meggondolásaink is, ugyanis G1 is O-ban adódik, továbbá H is. f1 viszont nem azonos g-vel, ezért G az O-tól különbözőnek adódik. Így E, F, G nem egy egyenesbe eső pontok, az EFG sík létezik és azonos e,g-vel. Ebben a helyzetben az OH egyenes határozatlannak látszik. Emlékezzünk azonban, hogy fent az OH egyenes nem O és H összekötésével jött létre, hanem mint a φ és γ síkok metszésvonala, ez pedig most is létezik: az O-ban e,g-re állított merőleges (ugyanis γ is, φ is merőleges e,g-re).
A már előre kizárt eseteken túl akkor sincs értelme a kérdésnek, ha az FG egyenes nem jön létre. F csak akkor nem jön létre, ha g1 merőleges f-re, mert így az e,f síkban az (O-tól különböző) E-ből g1-re állított merőleges párhuzamos f-fel. Ez azt jelenti, hogy g is merőleges f-re, tehát másrészt G sem jön létre. ‐ Ha F és G létrejött, akkor H is létezik.
 

Mindezeket összefoglalva a feltett kérdésre válaszunk: ha f és g nem merőlegesek és egyik egyenes sem merőleges a másik kettő síkjára, akkor az FG egyenes létrejön és merőleges e1-re; a kizárt esetekben a kérdésnek nincs értelme.
 
 Makai Endre (Budapest, Eötvös J. g. II. o. t.)
 

Megjegyzés. A legtöbb dolgozatban fel sem merül, hogy léteznek-e mindig a szóban forgó egyenesek.