Feladat: 1206. matematika feladat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Kászonyi László ,  Mészáros György 
Füzet: 1963/október, 55 - 57. oldal  PDF  |  MathML 
Témakör(ök): Másodfokú (és arra visszavezethető) egyenletrendszerek, Egyenesek egyenlete, Parabola egyenlete, Paralelogrammák, Parabola, mint mértani hely, Feladat
Hivatkozás(ok):Feladatok: 1962/november: 1206. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az y=ax2 parabola (a≠0) négy különböző pontja A(x1, ax12), B(x2, ax22), C(x3, ax32), D(x4, ax42). Itt x1, x2, x3, x4 különbözők, mert pl. x1=x2-ből A és B azonossága következnék, a feltevéssel ellentétben. Tegyük fel, hogy A, B, C, D egy paralelogramma csúcsai, azaz AB∥CD, és AD∥BC. Eszerint az összekötő egyenesek iránytényezőinek megegyezéséből:

ax22-ax12x2-x1=ax42-ax32x4-x3ésax42-ax12x4-x1=ax32-ax22x3-x2(1)
(Itt mindegyik tört nevezője 0-tól különböző.) Az (1) egyenlőségek kiemeléssel, szorzattá alakítással és egyszerűsítésekkel így alakulnak:
a(x22-x12)x2-x1=a(x2+x1)(x2-x1)x2-x1=a(x2+x1)=a(x4+x3),
tehát
x2+x1=x4+x3,és ugyanígyx4+x1=x3+x2,
ezekből pedig a megfelelő oldalak összeadásával és rendezéssel x1=x3 adódik, feltevésünkkel ellentétben. Ezért az (1) egyenlőségek egyidejűen nem állhatnak fenn, A, B, C, D nem alkothat paralelogrammát.
 
 Mészáros György (Budapest, Piarista g. III. o. t.)
 
 
1. ábra
 

II. megoldás. Tegyük fel, hogy a p parabolába beírt ABCD négyszög paralelogramma, és tükrözzük ábránkat a négyszög K középpontjára. Ekkor A, B, C, D rendre C, D, A, B-be megy át, p pedig egy p' parabolába. Így a p és p' paraboláknak legalább 4 különböző közös pontjuk van; másrészt tengelyeik párhuzamosak, mert a tükrözés p tengelyét egy vele párhuzamos egyenesbe viszi át. Ha p egyenlete y=ax2, a K pont koordinátái (α, β), akkor p' csúcsa (2α, 2β), tengelye az x=2α egyenes, és egyenlete y-2β=-a(x-2α)2.
Mármost p és p' közös pontjait keresve ezek abszcisszáit az egyenleteikből y kiküszöbölésével adódó
ax2=-a(x-2α)2+2β
egyenletből kapjuk. Ez másodfokú, tehát p-nek és p'-nek legfeljebb két abszcisszán lehet közös pontja. Másrészt p és p' egyenlete szerint minden x-hez csak egy y érték tartozik, így p és p' közös pontjainak a száma legfeljebb 2.
Ellentmondásra jutottunk fenti megállapításunkkal, tehát feltevésünk hibás, a parabolába nem írható paralelogramma.
 
 Kászonyi László (Szombathely, Nagy Lajos g. IV. o. t.)
 

III. megoldás. Bebizonyítjuk, hogy véve egy parabolának egy adott iránnyal párhuzamos húrjait, ezek felezőpontjai egy a parabola tengelyével párhuzamos egyenesen vannak rajta. Más szóval: ha egy a p parabolába beírt ABCD négyszög AB és CD oldalai párhuzamosak, akkor ezen oldalak felezőpontját G, ill. H-val jelölve a GH egyenes párhuzamos p-nek a tengelyével.
Ebből már következik a bizonyítandó állítás. Ha ugyanis ABCD paralelogramma volna, akkor az AB és CD oldalak felezőpontjait összekötő szakasz is, a BC és DA oldalak felezőpontjait összekötő szakasz is párhuzamos volna a-val, holott ez a két szakasz metszi egymást a paralelogramma középpontjában.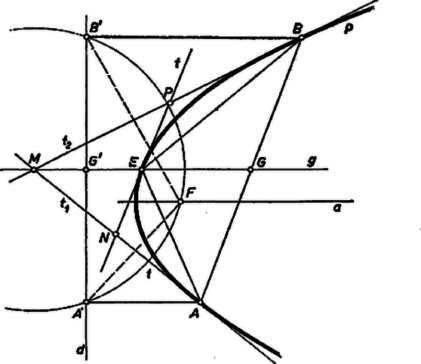
 
 
2. ábra
 

Legyen az A, B, G pontok vetülete a d vezéregyenesen rendre A', B', G', az A-ban és B-ben p-hez húzott érintő t1 ill. t2, metszéspontjuk M. Jelöljük a parabola gyújtópontját F-fel. Ismeretes, hogy t1 merőlegesen felezi FA'-t, és hasonlóan t2 az FB'-t, így M az A'B'F háromszög köré írt kör középpontja. Ezen átmegy a GG'=g egyenes is, ugyanis ABB'A' trapézban GG' középvonal, ezért G'-ben merőlegesen felezi A'B'-t. g párhuzamos a-val, így azt kaptuk, hogy a parabola egy húrjának felezőpontján át a tengellyel párhuzamosan húzott egyenes átmegy a húr végpontjaiban húzott érintők metszéspontján.
Legyen p-nek g-n levő pontja E, az ebben húzott érintő t, és messe ez t1-et N-ben, t2-t P-ben. A parabola imént talált tulajdonságát az EA, ill. EB húrra alkalmazva kapjuk, hogy N felezi MA-t, ugyanígy P felezi MB-t, hiszen pl. N rajta van az AE felezőpontján át a-val párhuzamosan húzott egyenesen, ami az AME háromszögnek ME-vel párhuzamos középvonala. Eszerint pedig NP az ABM háromszög AB-vel párhuzamos középvonala, vagyis t párhuzamos AB-vel. Ezzel azt kaptuk, hogy a parabola egy húrjának felezőpontján át a tengellyel párhuzamosan húzott egyenes átmegy a húrral párhuzamos érintő érintési pontján.
Eredményünk szerint a CD húr H felezőpontján át a tengellyel párhuzamosan húzott egyenes ugyancsak átmegy E-n, tehát azonos g-vel. Ezzel a bevezetésül kimondott állítást bebizonyítottuk, abból pedig ‐ mint láttuk ‐ következik, hogy az ABCD négyszög nem lehet paralelogramma.
 

Megjegyzés. A felhasznált segédtételt a koordinátageometria módszereivel is megkaphatjuk. Legyen a parabola egyenlete y=ax2, a párhuzamos húrok közös iránytangense m. Ekkor egy húr egyenese y=mx+b, és a húr két végpontjának abszcisszáit a két egyenletből y kiküszöbölésével adódó ax2-mx-b=0 egyenlet gyökei szolgáltatják. Ha ezen abszcisszák x1 és x2, akkor a felezőpont x0 abszcisszája a másodfokú egyenlet gyökei és együtthatói közötti, ismert összefüggés alapján
x0=x1+x22=m2a,
független b-től, és változatlan m mellett állandó, tehát minden m irányú húr felezőpontja egy az Y-tengellyel, a parabola tengelyével, párhuzamos egyenesen van rajta. ‐ Ha a fenti másodfokú egyenlet diszkriminánsa eltűnik: m2+4ab=0, akkor x1=x2, és az innen adódó b=-m2/4a értékkel az y=mx-m2/4a egyenes a parabola érintője, az érintési pontra is teljesül x1=x2=x0.