Kezdőlap


Feladat:	1205. matematika feladat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Lepsényi Edit , Szilágyi Tivadar
Füzet:	1963/szeptember, 15 - 16. oldal		PDF \| MathML
Témakör(ök):	Mértani középtételek derékszögű háromszögekben, Szögfelező egyenes, Algebrai átalakítások, Körülírt kör, Beírt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Feladat
Hivatkozás(ok):	Feladatok: 1962/november: 1205. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a három oldal mértékszámra rendre $a = b - 1$ , $b$ , $c = b + 1$ (ahol nyilván $b > 2$ ). Így a háromszög kerülete $2 s = 3 b$ , területe

\begin{matrix} t = \sqrt[]{\frac{3 b}{2} (\frac{b}{2} + 1) \frac{b}{2} (\frac{b}{2} + 1)} = \frac{b}{4} \sqrt[]{3 (b^{2} - 4)}, \end{matrix}

ennélfogva ismert összefüggések alapján a beírt és a körülírt kör sugara:

\begin{matrix} ϱ = \frac{t}{s} = \frac{\sqrt[]{3 (b^{2} - 4)}}{6}, r = \frac{a b c}{4 t} = \frac{b^{2} - 1}{\sqrt[]{3 (b^{2} - 4)}} . \end{matrix}

(1)

Ezekkel a vizsgálandó összefüggés jobb oldala

\begin{matrix} 2 ϱ + \frac{1}{2 ϱ} = \frac{4 ϱ^{2} + 1}{2 ϱ} = \frac{\frac{3 (b^{2} - 4)}{9} + 1}{\frac{\sqrt[]{3 (b^{2} - 4)}}{3}} = \frac{b^{2} - 1}{\sqrt[]{3 (b^{2} - 4)}}, \end{matrix}

egyenlő

r

kifejezésével. Tehát az állítás igaz.
A bizonyításban nem használtuk fel, hogy az oldalak mértékszámai egészek, ezért az összefüggés minden olyan háromszögben fennáll, melyben a legkisebb oldal 1-gyel kisebb, a legnagyobb oldal pedig 1-gyel nagyobb, mint a (nagyságra nézve) középső oldal.

Lepsényi Edit (Budapest, Berzsenyi D. lg. IV. o. t.)

Megjegyzés. Hasonló számítás mutatja, hogy ha az oldalak hossza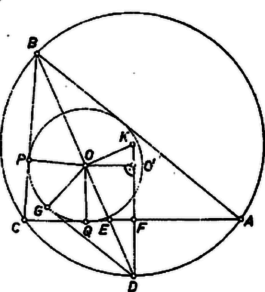

b - d

b

és

b + d

, akkor

\begin{matrix} r = 2 ϱ + \frac{d^{2}}{2 ϱ} . \end{matrix}

Ezt más úton mutatjuk meg. Ennek során kissé több számolással a vizsgált háromszögekben további érdekes összefüggéseket is fogunk találni.

II. megoldás. Legyen az

A B C

háromszögben

A C = b

B C = a = b - d

A B = c = b + d

, a körülírt kör középpontja

K

, sugara

r

, a beírt, kör középpontja

O

, sugara

ϱ

, érintési pontja a

B C

oldalon

P

A C

-n

Q

. Ismert összefüggés szerint

\begin{matrix} A Q = \frac{b + c - a}{2} = \frac{b}{2} + d, \end{matrix}

ha tehát

A C

felezőpontja

F

, akkor

F Q = A Q - A F = d

. Messe a

C B A

szög

B O

felezője az

A C

oldalt

E

-ben, a

B

-t nem tartalmazó

A C

ívet,

D

-ben.

B C < B A

miatt

E

C F

szakaszon, szűkebben a

Q F

szakaszon van. Megmutatjuk, hogy

E

felezi a

Q F

szakaszt. A szögfelező osztásarányára ismert tétel szerint

\begin{matrix} \frac{C B}{A B} = \frac{C E}{A E} = \frac{C F - E F}{A F + E F}, tehát \frac{b - d}{b + d} = \frac{\frac{b}{2} - E F}{\frac{b}{2} + E F} = \frac{b - 2 E F}{b + 2 E F}, \end{matrix}

és innen valóban

2 E F = d = Q F

D

felezi a mondott

A C

ívet, ezért

D F

merőleges

A C

-re és átmegy

K

-n. Így a

D E F

és

O E Q

derékszögű háromszögek egybevágók, mert egy-egy oldaluk és a rajta fekvő szögeik egyenlők, tehát

F D = Q O = ϱ

és

O E = D E

. Ezért,

O

-nak

K D

-n levő vetületét

O^{'}

-vel jelölve

D O^{'} = D F + F O^{'} = 2 Q O = 2 ϱ

, másrészt

O O^{'} = Q F = d

, és igy az

O D O^{'}

derékszögű háromszögből

\begin{matrix} O D^{2} = D O^{' 2} + O^{'} O^{2} = 4 ϱ^{2} + d^{2} . \end{matrix}

Érintse a beírt kört a

D

-ből húzott érintő

G

-ben, akkor az I. megoldás (1) összefüggéséhez hasonlóan adódó

12 ϱ^{2} = b^{2} - 4 d^{2}

egyenlőség felhasználásával

\begin{matrix} D G^{2} = O D^{2} - ϱ^{2} = 3 ϱ^{2} + d^{2} = \frac{b^{2}}{4}, D G = \frac{b}{2} . \end{matrix}

Így a

D O G

háromszög egybevágó a

B O P

háromszöggel, mert az utóbbiban

B P = (a + c - b) / 2 = b / 2

, ennélfogva

B O = D O

. Eszerint

O

felezi a körülírt kör

B D

húrját, és a

D K O

háromszög

O

-nál derékszögű. Ebből az ismert mértani középarányos tétel alapján

\begin{matrix} D O^{'} \cdot O^{'} K = O O^{' 2}, 2 ϱ (r - 2 ϱ) = d^{2}, \end{matrix}

ami a bizonyítandó összefüggésnek átrendezett alakja. Ezzel a bizonyítást befejeztük.

Szilágyi Tivadar (Budapest, II. Rákóczi F. g. III. o. t.)