| Feladat: | 1202. matematika feladat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Csirik János , Márki László | ||
| Füzet: | 1963/május, 205 - 206. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Algebrai átalakítások, Geometriai egyenlőtlenségek, Terület, felszín, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1962/november: 1202. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Legyen , . Ekkor , a háromszög -ra merőleges magassága . Ekkor ‐ az idomok területét ugyanúgy jelölve, mint magukat az idomokat ‐ a következő egyenlőtlenség fennállását kell bizonyítanunk: 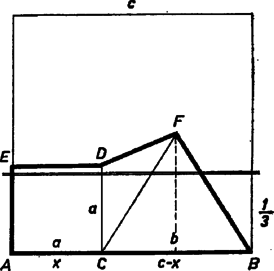 Az első két tagból teljes négyzetté kiegészítéssel tehát a különbség II. megoldás. Legyen , , így és az I. megoldás szerint az ötszög területe: Egyszerűbb számolás érdekében jelöljük , , együtthatóját átmenetileg rendre , , -rel, így . Kiemeléssel és teljes négyzetté kiegészítéssel illetőleg az együtthatókkal a számításokat elvégezve |