Kezdőlap


Feladat:	1199. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Cserháti György , Forgó Antal , Lőrincz Csaba
Füzet:	1963/november, 113 - 115. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Szögfelező egyenes, Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek szerkesztése, Szögfüggvények, síkgeometriai számítások, Feladat
Hivatkozás(ok):	Feladatok: 1962/október: 1199. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a keresett $A B C$ derékszögű háromszög átfogója $A B$ , és messe a $B A C$ szög felezője $B C$ -t $D$ -ben. A háromszöget az $A D = f$ és $B D = q$ szakaszokból kell megszerkesztenünk (ugyanis 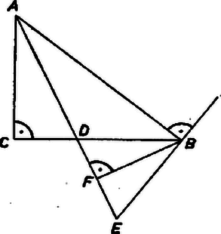$B D > C D$ , hiszen $B D : C D = A B : A C > 1$ ).
Messük el $A D$ -t az $A B$ átfogóra $B$ -ben állított merőlegessel (1. ábra), másrészt a $B$ -ből $A D$ -re bocsátott merőlegessel; legyenek a metszéspontok $E$ és $F$ . A $B D E$ háromszög egyenlő szárú, mert $E$ -nél levő belső szöge a $B A E$ szöget egészíti ki $90^{\circ}$ -ra, $D$ -nél levő szögének csúcsszöge pedig a $C A E$ szöget, és ezek a $B A C$ szög felével egyenlők. Így $B E = B D = q$ és $F$ felezi a $D E$ szakaszt.

1. ábra

A E B

derékszögű háromszögben a befogó mértani közép tulajdonsága szerint

\begin{matrix} A E \cdot E F = B E^{2}, \end{matrix}

vagy

\begin{matrix} A E \cdot D E = 2 A E \cdot E F = (f + D E) D E = 2 q^{2} . & (1) \end{matrix}

Ebből az összefüggésből

D E

, és annak ismeretében a keresett háromszög megszerkeszthető pl. a következő módon. Rajzoljunk

q

befogójú egyenlő szárú derékszögű háromszöget (

E B G

E B = B G = q

, 2. ábra), és ennek átfogóját

G

-ben érintő

f / 2

sugarú

k

kört. Az

E

-n és

k

középpontján átmenő egyenes

E

-hez közelebbi és távolabbi metszéspontja legyen

D_{1}

és

A_{1}

. Ekkor

\begin{matrix} E D_{1} \cdot {E A}_{1} = E D_{1} (E D_{1} + f) = E G^{2} = 2 q^{2} . \end{matrix}

(2)

Messük a

G B

egyenest az

E

középpontú,

A_{1}

-en átmenő körrel, egyik metszéspont legyen

A

, és messük

E A

-t a

B

középpontú,

q

sugarú körrel

D

-ben. Legyen

A

merőleges vetülete

B D

-n

C

, ekkor az

A B C

háromszög megfelel a feltételeknek.

Ez a következő módon látható.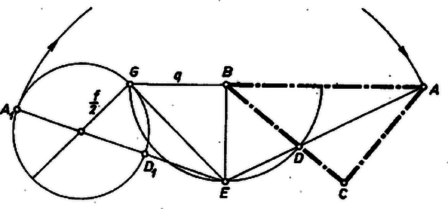

\begin{matrix} A_{1} G E ∢ > A_{1} G D_{1} ∢ = 90^{\circ}, így A_{1} E > G E = \sqrt[]{2} q, \end{matrix}

amiből következik, hogy

A B > q

, tehát

D

E A

szakaszra,

C

pedig a

B D

szakasz

D

-n túli meghosszabbítására esik.

A D

felezi a

B A C

szöget, mert

B A D ∢ + B E A ∢ = C A D ∢ + A D C ∢ = 90^{\circ}

, de

A D C ∢ = E D B ∢ = D E B ∢

, mivel a

B D E

háromszög szerkesztés szerint egyenlő szárú:

B D = B E = q

2. ábra

Azt kell még belátnunk, hogy

A D = f

. A 2. ábra

A

B

C

D

E

pontjai kielégítik ugyanazokat a feltételeket, mint az 1. ábráéi, így

A E \cdot D E = 2 q^{2}

, de szerkesztés szerint

A E = A_{1} E

, s így (2)-t is figyelembe véve

A E \cdot D E = A_{1} E \cdot D E = 2 q^{2} = A_{1} E \cdot D_{1} E

, vagyis

D E = D_{1} E

, és

A D = A E - D E = A_{1} E - D_{1} E = A_{1} D_{1} = f

.
Könnyen látható, hogy a szerkesztés mindig elvégezhető, és egyetlen megoldása van.

Megjegyzés. Lényegében az (1) összefüggéshez jutunk a következő úton is. Az

A D

egyenes az

A B C

háromszög köré írt kör

A

-t nem tartalmazó

B C

ívét annak

F

felezőpontjában metszi. (Ez a pont azonos a fenti

F

-fel, mert utóbbiból

A B

derékszög alatt látszik, s így ez a pont rajta van a körülírt körön is,

A D

-n is. Ennek folytán

F D = E D / 2

.) Ezért

F A C △ \sim F C D △

, mert

F

-nél közös szögük van, továbbá

F A C ∢ = F A B ∢ = F C B ∢

. Így

F A : F C = F C : F D

F D \cdot F A = F D

(F D + f) = F C^{2} = F B^{2} = B D^{2} - F D^{2} = q^{2} - F D^{2}

, amiből átrendezéssel és szorzással

\begin{matrix} F D (2 F D + f) = q^{2} \\ 2 q^{2} = 2 F D (2 F D + f) = E D (E D + f) . \end{matrix}

Cserháti György és Forgó Antal (Eger, Gárdonyi G. g. IV. o. tanulók)

A versenyzők legnagyobb része a szerkesztést több számítás alapján végezte el, ilyen a következő.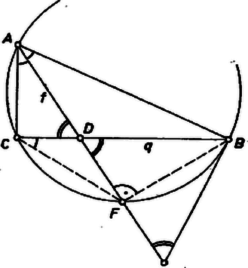

3. ábra

II. megoldás.

B A C ∢ = α

jelöléssel az

A B D

háromszögből a szinusz tétellel

\begin{matrix} \frac{f}{q} = \frac{sin (90^{\circ} - α)}{sin \frac{α}{2}} = \frac{cos α}{sin \frac{α}{2}} = \frac{1 - 2 sin^{2} \frac{α}{2}}{sin \frac{α}{2}}, \end{matrix}

miből ‐ az egyenletnek csak a pozitív gyökét véve ‐

\begin{matrix} 2 q sin^{2} \frac{α}{2} + f sin \frac{α}{2} - q = 0, \\ sin \frac{α}{2} = \frac{\sqrt[]{f^{2} + 8 q^{2}} - f}{4 q}, \\ F D = q sin \frac{α}{2} = \sqrt[]{{(\frac{f}{4})}^{2} + {(\frac{q}{\sqrt[]{2}})}^{2}} - \frac{f}{4} . \end{matrix}

Ez a kifejezés egyszerűen megszerkeszthető, ugyanis a

q / \sqrt[]{2}

szakasz egyenlő a

q

oldalú négyzet köré írható kör sugarával ‐, tovább az előző megoldás szerint haladhatunk.

Lőrincz Csaba (Orosháza, Táncsics M. g. III. o. t.)